新型混合励磁直驱式风力发电系统MPPT控制

赵梅花 杨 勇 钟沁宏

（1. 洛阳理工学院机电工程系 洛阳 471023 2. 上海大学机电工程与自动化学院 上海 200072 3. 苏州大学城市轨道交通学院 苏州 215021）

1 引言

典型的风力发电系统结构有双馈风力发电系统和直驱式永磁同步风力发电系统[1,2]。双馈发电系统具有投资少、功率损耗低等优点，其不足之处是需要齿轮箱，可靠性低[3,4]。直驱式永磁同步风力发电机系统采用发电机与叶轮直接相连的驱动方式，省去了齿轮箱，可靠性和效率较高，但由于其磁场不可控，风能的最大功率跟踪控制较为复杂[5,6]。

混合励磁同步发电机（Hybrid Excitation Synchro-nous Generator，HESG）是在传统永磁同步电机基础上增加了可调节的电励磁环节，不仅具备永磁电机的优点，而且可实现电机气隙磁场平滑可调。发电运行时，具有较宽的电压调节能力或宽范围变速恒压输出能力，具有广泛的工业应用前景。

基于HESG的直驱式风力发电系统具有磁场可调、转矩密度高、效率高等优点，易于实现系统最大风能跟踪控制的特点[7,8]。

直驱式永磁同步风力发电系统中，由于永磁电机本身励磁不可控，需在主电路添加电力电子装置辅助实现最大风能跟踪[9-12]。基于 HESG的直驱式风力发电系统，可通过调节电励磁电流的大小实现风能最大捕获，不需增设硬件电路。文献[13]提出了基于最佳叶速比的最大风能跟踪方案，根据检测的风速调节HESG的转速，使风机运行于最佳叶尖速比，从而捕获最大风能，控制简单，易于实现，但该控制依赖于风机参数和空气密度，且实际风场的风速测量不仅会增加成本，测量精度也难以保证。

本文提出了变步长最大风能跟踪（Maximum Power Point Tracking，MPPT）控制算法，该算法不依赖风机参数和空气密度。算法实现时HESG工作于速度控制模式，转速环给定ω*随着两个连续采样周期有功功率变化ΔP的幅值和正负做动态调整，自动搜索风机在该风速下的最佳转速点，实现最大风能跟踪。搭建了基于HESG的直驱式风力发电系统实验平台，实验结果验证了所提MPPT算法的可行性和正确性。

2 系统结构

基于 HESG的直驱式风力发电系统如图 1所示。系统由风轮机、HESG、三相不控整流桥、并网逆变器等组成。HESG将风能转换为正弦交流电能，再由三相不控整流桥转换为直流电储存于母线电容，通过三相并网逆变器逆变并网。HESG与风机直接相连，采用小容量励磁调节装置（本系统采用Buck电路）控制HESG的励磁电流，降低了成本，提高了系统的效率和可靠性。

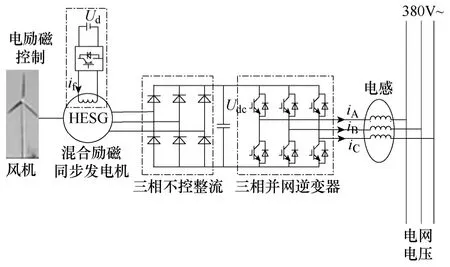
图1 混合励磁风力发电系统结构Fig.1 Schematic block diagram of System

本课题研究采用台达环境与教育基金会《电力电子科教发展计划》（DRES2007002）资助研发的新型混合励磁同步发电机，其结构如图2所示[14]。装在定子上的直流励磁线圈首先在旋转的转子上感应出交流励磁电流，又经转子上的整流器给位于转子上的励磁绕组励磁，和永磁体共同产生气隙磁场，在定子上感应出电动势。由于发电机的气隙磁场由永磁体和电励磁共同产生，通过调节电励磁绕组中直流电流来调节气隙磁场的大小，实现磁场平滑可调。

图2 HESM结构图Fig.2 Schematic diagram of HESM

3 HESG数学模型及励磁控制

取由定子绕组端点流入电机中心方向作为定子各相电流的参考正方向，绕组磁链ψ和电流i的正方向符合右手螺旋法则，永磁体产生的主极磁通方向定为 d轴的正方向，q轴超前 d轴 90°电角度。HESG在dq坐标系下的方程如下[14]。

电枢绕组和励磁绕组的磁链方程

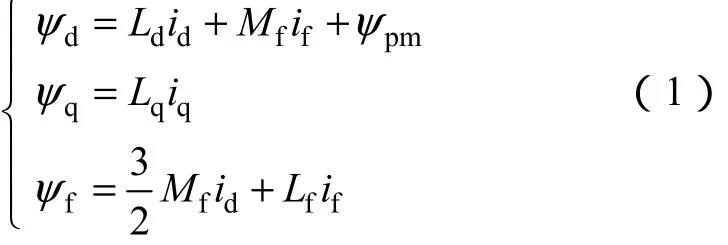
式中，Ld、Lq分别为直轴和交轴电感；Mf为励磁绕组与电枢绕组的互感；Lf为励磁绕组自感；ψpm为永磁体匝链电枢绕组的磁链幅值。

电压方程

由方程（2）可知，控制励磁电流的大小，即可控制定子电压和定子电流的大小。方程（2）中励磁回路电压方程是励磁电流控制策略电流内环的设计依据。

本文由Buck电路为 HESG电励磁，为了保证磁场稳定，采用励磁电流闭环控制。

4 MPPT控制算法

系统控制环节主要由并网逆变控制和最大风能跟踪控制构成。并网逆变器采用电网电压定向的矢量控制策略[13]，主要控制目标是保持直流母线电压恒定，实现有功和无功功率的解耦控制及逆变并网。限于篇幅，本文仅对最大风能跟踪控制做详细阐述，并网逆变控制策略仅配合所提出的MPPT算法做实验验证。

MPPT控制算法主要有极值搜索法和最佳功率—转速曲线法两大类[15,16]。无论采用哪种 MPPT算法，其实质都是依据风机基本特性。本文提出一种变步长MPPT算法，通过试验得出一种更有效的步长经验计算方法。

4.1 风机基本特性

根据贝茨（Betz）理论，风机捕获风能Pwind为

式中，ρ为空气密度；R为叶片半径；v为风速；CP(β,λ) 为风能利用系数，是桨叶节距角β和叶尖速比λ(λ=Rω/v) 的函数，它反映了风机将风能转化为机械能的效率。

在定桨距（β固定）情况下，本实验所模拟风机的CP(β,λ) 曲线如图 3所示。调节ω使风机达到最佳叶尖速比λopt(λopt=3.7，CP=CP-max)，实现最大风能捕获。定桨距风机Pwind(ω,v) 曲线如图4所示。

图 3 CP(λ) 曲线Fig.3 CP(λ) characteristics curve

图 4 定桨距风机Pwind(ω,v) 曲线Fig.4 Pwind(ω,v) curve of imitation wind turbine

4.2 变步长MPPT算法

变步长极值搜索法采用步长随风机运行点位置自动调节的机制，能快速、准确地达到最佳工作点。其算法原理通过图4来阐述。

变步长搜索法转速增量（步长）表达式为

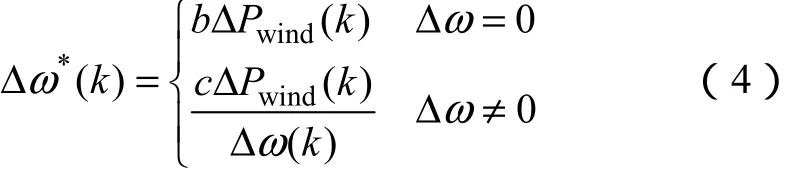
式中，ΔPwind(k)、Δω(k) 分别为连续两次算法周期之间风机输出功率和风机转速的增量；b、c为变步长爬山算法权值，它们影响变步长算法的速度和精度，需根据实际系统选取。

式（5）是本文根据实验现象得出的步长经验算法。由于步长给定Δω*(k) 的大小和方向是由ΔPwind(k)和Δω(k)的大小和正负共同决定的，用此式计算步长更为合理，使系统能快速准确地搜索到最大风能捕获点。

根据Δω*(k) 和转速ω(k-1) 算出 HESG 转速给定为

变步长搜索法的工作过程可根据图 4描述如下：

图5 变步长算法流程Fig.5 Flow chart of algorithm

4.3 变步长MPPT算法实现

变步长自动搜索法的核心是对ΔPwind和Δω的测量，Δω可以通过光电码盘等测速装置测得，但ΔPwind很难直接测得。整个系统的功率是由风机流向电网，根据功率平衡原理得

式中，J和Tf为传动机构惯性时间常数和摩擦转矩；P1为逆变器输出有功功率；Ploss为系统损耗。对于中小功率发电系统，忽略J、Tf和Ploss的影响，则有

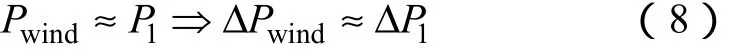
通过检测一定间隔时间内的ΔP1近似得到ΔPwind，由式（4）得到转速给定信号ω*。

转速、电流双闭环变步长MPPT控制结构如图6所示。

图6 MPPT算法结构Fig.6 Schematic diagram of MPPT algorithm

5 实验及结果分析

5.1 实验平台的搭建

搭建了如图 7所示的直流电机-混合励磁发电机风力发电系统实验平台。实验所用HESM参数见表1。用3kW直流电机模拟风机特性，被模拟风机CP(λ) 模型为

图7 实验平台结构Fig.7 Structure of test platform

表1 HESG参数Tab.1 Parameters of the HESG

取表2的风机参数并与实验室3kW直流电动机的输出功率、转速匹配，引入虚拟传动比1:2.151，模拟结构如图8所示。模拟风机Pwind(ω,v) 曲线如图4所示，风速范围为9～15m/s。因风机模型的最佳叶尖速比λopt=3.7，由叶尖速比的定义和虚拟齿轮传动比可知，当HESG转速与风速之间满足式（10）时，模拟风机输出该风速下最大功率。

表2 定桨距风机模拟参数Tab.2 Imitation parameters of wind turbine

图8 直流机模拟定桨距风机控制策略Fig.8 Emulation scheme of the wind turbine

5.2 实验结果分析

在风机特性模拟的基础上，进行系统的最大风能跟踪和并网逆变试验。

变步长算法的采样周期为 1.2s，HESG转速环调节周期为 1ms，用试凑法得到步长权值b为0.4rad2/(W⋅s2)，c为 0.3rad2/(W⋅s2)。采用 infineon X167C作为系统的主控芯片，并网逆变器PWM频率 10kHz。直流母线电压 500V，电网电压300V。实验波形如图9～图12所示。

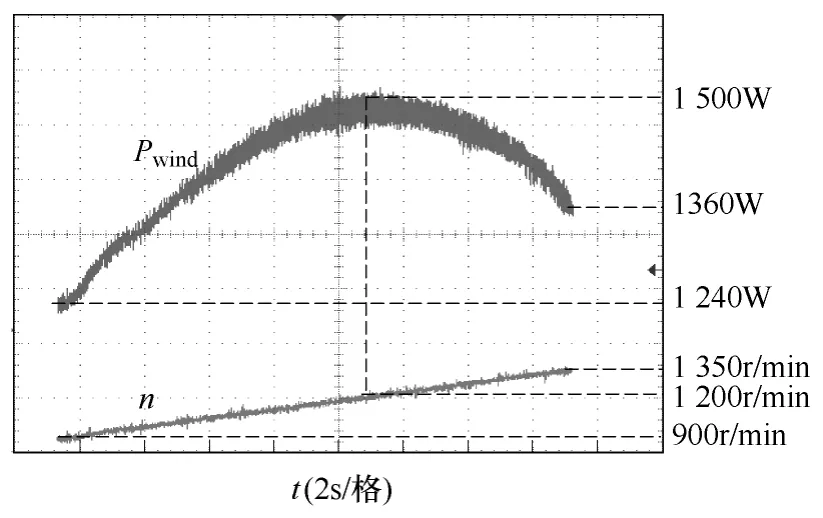
图9 模拟风机的 P(ω) 曲线（v=12m/s）Fig.9 P(ω) curve of emulated wind turbine

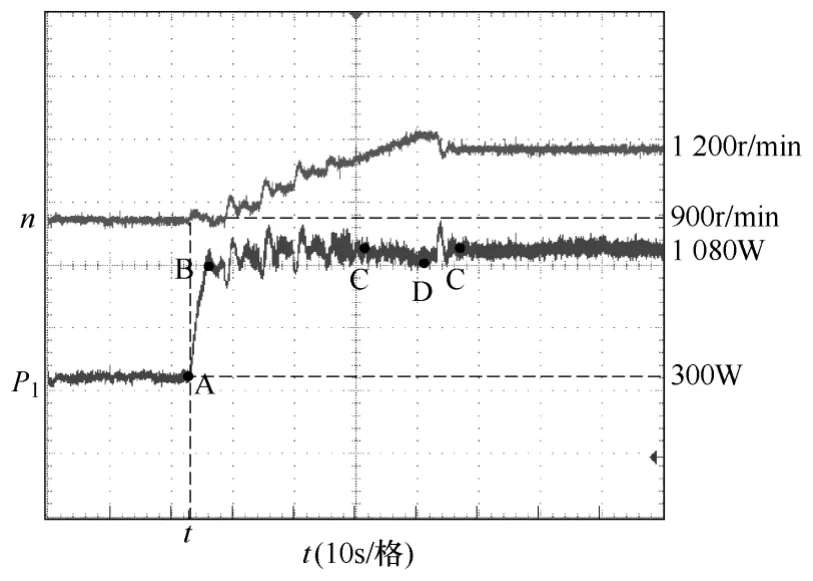
图10 算法跟踪过程Fig.10 Tracking process of algorithm

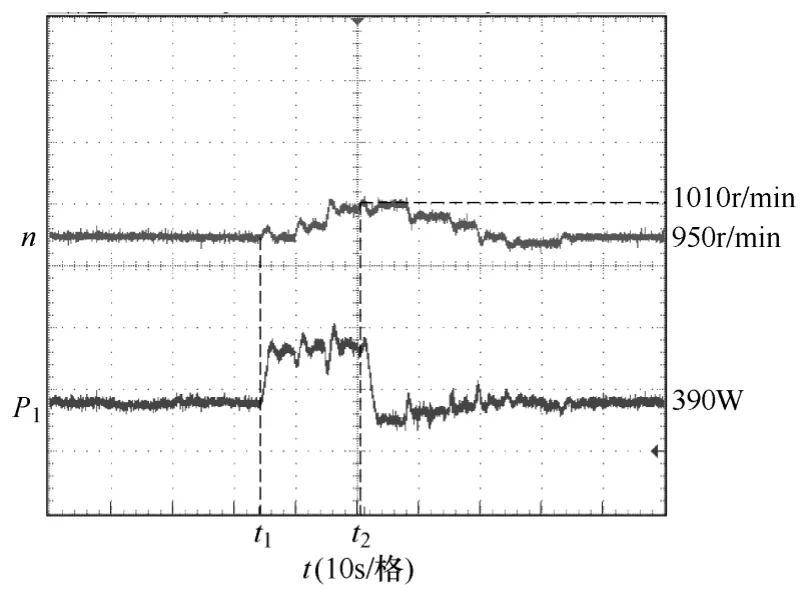
图11 算法动态响应Fig.11 Dynamic response of algorithm

图12 v=12m/s不同功率因数下逆变波形Fig.12 Inverter waveforms in different cosφ, v=12m/s

图 9所示的直流机Pwind（ω,v）曲线与被模拟风机的转速-功率曲线（图4）一致，当风速为12m/s时，HESG转速为1 200r/min时风机捕获最大功率，验证了当HESG转速和风速满足式（10）关系时，模拟风机输出该风速下的最大功率。

图10是变步长算法的跟踪过程。在t时刻阶跃改变风速v(9m/s→12m/s) 时（图4所示），由于系统惯性，转速n不能突变，Pwind从点A→B突增，这时转速增加，步长为bΔPwind(k)，之后步长为cΔPwind(k) /Δω(k)，从点B→D系统通过变步长算法调节发电机转速，且步长Δω越来越小地逼近最大风能点C，若步长合适，可使系统稳定运行于C点，若步长较大使系统运行到D点时， ΔPwind为负值，Δω*也随之变为负值，转速下降，功率增加，即ΔPwind为正，运行点左移，通过变步长算法最后稳定运行于 D点，满足式（10）关系的最佳转速ωopt=±1 0r/min 范围内。Pwind为模拟风机输出最大功率的基础上除去Ploss的P1观测值。

图 11验证了采用变步长算法系统的动态响应能力。在t1时刻改变风速v（9.5m/s→11m/s），系统进入最大风能跟踪控制，通过变步长搜索算法，系统转速逐渐向最佳转速调节，在系统未达稳态的t2时刻再次改变风速v（11m/s→9.5m/s），系统搜索方向能够快速响应风速变化并最后稳定运行于最佳转速附近，验证了系统对快变风速的动态响应能力。

本系统最大风能跟踪范围为 9～15m/s。图 12是风速为12m/s时，在不同功率因数下的逆变波形，uga为a相电网电压波形，ia为a相逆变电流波形。

实验结果表明，系统能在一定风速范围顺利实现变步长MPPT算法和并网逆变。验证了控制策略的正确性。

6 结论

本文将HESG应用于直驱式风力发电系统。导出了 HESG在 dq坐标系下的数学模型，对系统控制机理进行了较为深入的研究。提出变步长 MPPT控制算法。该算法不依赖风机参数和空气密度，自动搜索风机在实时风速下的最佳转速点，实现最大风能跟踪。对变步长MPPT算法的跟踪过程作了详细阐述，通过实验得出一种变步长经验算法，使系统更有效地实现最大风能跟踪，提高了发电系统的运行效率。在一定风速范围内，系统能很好地实现最大风能跟踪和并网逆变。

[1] Carrasco J M, Franquelo L G, Bialasiewicz J T, et al.Power-electronic systems for the grid integration of renewable energy sources: a survey[J]. IEEE Transactions on Industrial Electronics, 2006, 53(4): 1002-1016.

[2] S Heier. Grid integration of wind energy conversion systems[M]. Hobo-ken, NJ: Wiley, 1998.

[3] Tapia A, Tapia G, Ostolaza J X, et al. Modeling and control of a wind turbine driven doubly fed induction generator[J]. IEEE Transactions on Energy Conversion, 2003, 18(2): 194-204.

[4] 苑国锋, 柴建云, 李永东. 变速恒频风力发电机组励磁变频器的研究[J]. 中国电机工程学报, 2005,25(8): 90-94.Yuan Guofeng, Chai Jianyun, Li Yongdong. Study on excitation converter of variable speed constant frequency wind generation system[J]. Proceedings of the CSEE, 2005, 25(8): 90-94.

[5] Gao J, Lu J, Huang K, et al. A novel variable step hill-climb search algorithm used for direct driven PMSG[C]. ICEET '09 International Conference on Energy and Environment Technology, 2009,Changsha: 511-514.

[6] Yiguang Chen, Zhiqiang Wang, et al. A control strategy of direct driven permanent magnet synchronous generator for maximum power point tracking in wind turbine application[C]. International Conference on Electrical Machines and Systems, 2008: 3921-3926.

[7] 夏永洪, 王善铭, 邱阿瑞, 等. 新型混合励磁永磁同步电机齿谐波电动势的协调控制[J]. 电工技术学报, 2012, 27(3): 56-61.Xia Yonghong, Wang Shanming, Qiu Arui, et al.Coordinated control of tooth harmonic EMF of novel hybrid excitation permanent magnet synchronous machine[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 56-61.

[8] Eftichios Koutroulis, Kostas Kalaitzakis. Design of a maximum power tracking system for wind-energyconversion applications[J]. IEEE Transactions on Industrial Electronics, 2006, 53(2): 486-494.

[9] Shuhui Li, Haskew T A. Characteristic study of vector-controlled direct driven permanent magnet synchronous generator in wind power generation[C].Power Engineering Society General Meeting, 2008,20-24: 1-9.

[10] Srighakollapu N, Sensarma P S. Sensorless maximum power point tracking control in wind energy generation using permanent magnet synchronous generator[C]. Industrial Electronics 34th Annual Conference of IEEE, 2008: 2225- 2230.

[11] Esmaili R, Xu L, Nichols D K. A new control method of permanent magnet generator for maximum power tracking in wind turbine application[C]. Power Engineering Society General Meeting, California(USA), 2005: 2090-2095.

[12] Chen Yiguang, Wang Zhiqiang, Shen Yong huan, et al.A control strategy of direct driven permanent magnet synchronous generator for maximum power point tracking in wind turbine application[C]. International Conference on Electrical Machines and Systems, 2008:3921-3926.

[13] 赵梅花, 阮毅, 杨勇, 等. 直驱式混合励磁风力发电系统控制策略的研究[J]. 电力系统保护与控制,2010, 38(12): 19-23.Zhao Meihua, Ruan Yi, Yang Yong, et al. Control strategy study on direct-driven type hybrid excitation wind power system[J]. Power System Protection and Control, 2010, 38(12): 19-23.

[14] 黄苏融, 张琪, 谢国栋, 等. 《多重电枢混合励磁直驱式风力发电系统》[P]. 中国发明专利申请, 2007.3.10.

[15] Li Chunhua, Zhu Xinjian, Sui Sheng, et al. Maximum power point tracking of a photovoltaic energy system using neural fuzzy techniques[J]. Journal of Shanghai University, 2009, 13(1): 29-36.

[16] Srighakollapu N, Sensarma P S. Sensorless maximum power point tracking control in wind energy generation using permanent magnet synchronous generator[C]. 34th Annual Conference of IEEE Industrial Electronics, Nov.10-13, 2008: 2225-2230.