考虑运行可靠性的含风电电力系统优化调度

胡国伟 别朝红 王锡凡

（电力设备电气绝缘国家重点实验室（西安交通大学电气学院） 西安 710049）

1 引言

随着能源和环境危机的加剧，风能利用成为国内外研究的热点。风电的并网运行是风能利用的发展趋势。由于风电是绿色可再生能源，电力公司应该首先调度全部的风电，然后再考虑调度其他传统的机组。可是风电具有不确定性和随机性的特点，如何考虑含风电电力系统优化调度成为国内外研究的焦点。

传统的电力系统优化调度分为静态优化调度和动态优化调度。动态优化调度考虑调度周期内各个时间段之间的联系，可以较合理地反映系统的运行情况。由于风电是随机变化的，用含风电电力系统的动态优化调度更加符合实际的要求。

电力系统可靠性按照不同的目的分为规划可靠性和运行可靠性。规划可靠性目的是为设计人员在电源的设计和线路的铺设计划中提供科学指导；运行可靠性是为运行人员的运行调度决策提供可靠性判断依据，从而提高电力系统运行的可靠性、安全性和经济性。

含风电电力系统优化调度，关键在于控制，由于风电的时序波动性和不确定性对系统带来的运行风险。文献[1, 2]将风电场风险权重系数或者风险系数引入到模型中，并作为风险成本加入到目标函数中。文献[3]将一定比例的风电场出力作为额定的备用需求加入到常规备用需求中。文献[4]引入风电预测误差对系统正负旋转备用的需求。文献[5-7]将风电出力作为随机变量，应用随机规划理论建立了含风电电力系统优化调度模型，在目标函数和约束条件中都描述了风电带来的不确定性。文献[8]是将风电出力作为模糊变量，建立优化调度的模糊模型。目前，从运行可靠性的角度研究电力系统优化调度模型，文献[9]建立了电力市场下综合考虑发电系统运行可靠性和旋转备用效益的优化调度模型。文献[10]将运行可靠性约束以近似解析表达的方式引入，完成了概率备用约束的优化调度。文献[11]研究了不同的风电装机容量，不同的负荷水平以及不同的前导时间（leading time）下，风电并网对电力系统运行可靠性的影响。但是由于当前国内外还没有建立相关指标的标准，这些文献也就停留在计算运行可靠性指标或者设定了比较粗略的指标标准，难以在实际系统中有效应用，以达到经济合理地解决风电并网带来的系统可靠性不足的隐患。

本文建立了时序多状态风电功率输出模型，准确地刻画风电时序性和波动性的特征。从运行可靠性的角度，深入分析风电并网对电力系统优化调度方案的影响，一方面风电并网替代了传统的耗能机组，可以使系统的总运行费用下降；另一方面，由于风电具有波动性和间歇性，容量可信度低，会导致系统的运行可靠性下降。为了应对风电并网的负面作用，本文建立了考虑运行可靠性的含风电电力系统优化调度模型。为突破当前国内外在运行可靠性应用方面还没有运行可靠性标准的局限，本文提出了含风电电力系统优化调度新策略，即在风电并入系统时，确保每一时段的运行可靠性至少不低于不含风电时系统的最低可靠性指标的优化调度策略。在模型求解上，通过数学变换，将非凸高次MIP模型，转化为凸二次MIP模型，然后运用优化软件Cplex的MIP优化器求解变换后的优化调度模型。IEEE RTS-96算例结果表明本文提出的优化调度新策略和求解算法的有效性和实用性以及对电力系统优化调度受风电影响分析的合理性。

2 时序多状态风电场功率输出模型

风电场常用的模型有两种。一种是等效多状态机组模型[12]，就是把风电功率输出等值为多状态机组。这样可以较好地考虑风电的波动性，但是忽略了风电的时序性。另一种是负荷修正器模型[13,14]，也就是把风电功率看做“负”负荷，这样可以较好地考虑风电的时序性，但是对风电的波动性考虑不足。综合两种模型的优点，建立了时序多状态风电功率输出模型,可以准确地反映每一时段风电的波动特性，适合电力系统优化调度研究。该模型的具体建立过程如下：

按照日前调度的需求，将调度周期分成24个时段，第t时段内风电场预测的离散风速数据序列为{vt1,vt2,vt3, …,vtNt}，其中t=1, 2, 3, …, 24，Nt为项数，对应每个风速，由风机有功功率输出特性计算得到风电场的输出功率预测值，因此可求得在i阶段内风电场输出功率的序列{pt1,pt2,pt3, …,ptNt}（该序列可能存在相同的值），剔除{pt1,pt2,pt3, …,ptNt}中的相同项，并按从小到大的顺序重新排序得到新的序列{Ct1,Ct2, …,CtMt}，由于{pt1,pt2,pt3, …,ptNt}中可能存在相同的值，{Ct1,Ct2, …,CtMt}的项数Mt≤Nt。{Ct1,Ct2, …,CtMt}序列中各项值为风电场在第t时段内输出功率各状态值，按照概率的古典定义，其概率可以用式（1）得到。

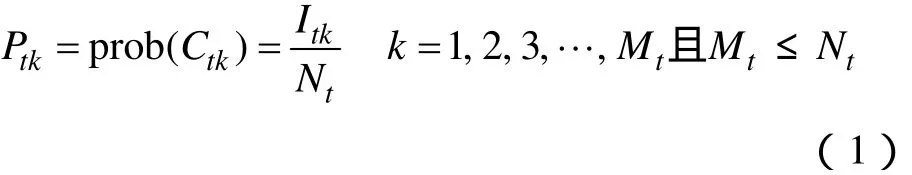
式中，Itk表示第t时段输出功率序列{pt1,pt2,pt3, …,ptNt}中值等于Ctk的项数；Ptk表示功率为Ctk的概率。

通过上述过程，可以得到时序多状态风电场功率输出模型见表 1，即每个时段t的风电功率输出有Mt个状态，每种状态的概率为Ptk。

表1 时序多状态风电场功率输出模型Tab.1 Time sequential multi-state wind farm power output model

风电场采用时序多状态模型时，综合了风电功率的时序性和波动性两大特征，合理地反映了风电功率的特点；但是由于在每个时段内，风电场的输出功率状态及相应概率都不同，因此该方法需要对调度周期内的每个时段都进行计算。

3 考虑风电的电力系统优化调度模型

3.1 传统的含风电电力系统优化调度模型

目标函数

目标函数有发电成本和机组启停成本两部分组成。风电不消耗一次能源，不计入成本。式中，F为系统总的运行费用；T为系统调度期间的时段数；I为系统机组数；pi(t)为机组i在t时段的有功功率；zi(t)为机组i在t时段的状态，zi(t)=1表示开机，zi(t)=0表示停机；Ci(pi(t))为机组i在t时段的运行费用

Si为机组i的开机费用；ai、bi、ci为机组的运行费用参数，为常数。

约束条件如下：

（1）功率平衡约束

式中，pw(t)为风电场t时段的平均输出功率；pd(t)为系统t时段的总负荷。

（2）发电机组输出功率上下限约束

（3）发电机爬坡约束

式中，rui、rdi分别表示发电机组i的向上和向下爬坡功率，MW/min；T60为表示时间是60min。

（4）最小运行时间和最小停运时间约束

（5）旋转备用约束

式中，URi为机组i的有功功率上升量上限，URi=ruiT10；T10表示时间是 10min；R(t)为t时刻系统的10min最小旋转备用要求，不同的系统规定不同。本文取最大单机容量。

3.2 风电并网对电力系统优化调度的影响

风电相比较其他传统机组，具有优先并网的优势。在电力系统优化调度时，风电的这种优势，会对传统机组产生“替代效应”，即会使得原来可以并网的部分机组功率被风电所替代，从而影响到了系统优化调度的结果。风电的“替代效应”具有两面性。正面影响是由于风电是不消耗一次能源的绿色可再生能源，它替代了传统的机组，可以减少系统的总运行费用；从运行可靠性的角度分析，负面影响就是使系统的机组投运风险度上升。原因是风电具有时序波动的特征，导致风电容量可信度[15,16]（wind capacity value，也称为 wind capacity credit，容量可信度指给定的发电机对全系统容量充裕度的贡献值）低于传统机组，风电对传统机组的替代，会使得传统的电力系统优化调度的结果存在着系统容量充裕度不足的问题，其实质就是使系统的机组投运风险度水平偏高，系统的运行存在着潜在的可靠性隐患。所以有必要针对这个问题采取相应的措施和提出合理的解决方案，控制含风电电力系统的运行风险。

运行可靠性的指标有两个：机组的投运风险度和响应风险度[17]。

投运风险度就是计算故障的发电容量还不能被替代的时间（即前导时间）内，已投运的发电容量刚好满足或刚好不满足期望负荷的概率。运行人员必须在前导时间开始时就意识到，如果负荷突然增长，那么直到前导时间结束以前，都将不可能替代任何失效机组或启动其他机组[18,19]。投运风险度可以反映在前导时间内发电容量的充裕度。系统前导时间一般为 1～4h。投运风险度数值越小，系统的风险度越小，运行可靠性越高。

响应风险度是计算在给定的响应时间内系统的备用容量刚好满足或刚好不满足期望响应容量的概率。由于风电场不做备用，所以只考虑运行可靠性中投运风险度，不考虑响应风险度。

3.3 考虑运行可靠性的含风电电力系统优化调度

3.1节给出了传统的含风电电力系统优化调度模型。该模型没有考虑风电的不确定性对系统运行带来的巨大风险。目前已有许多文献对此模型进行改进，但都没有从风电时序波动的基本特征出发，研究风电对优化调度运行风险的影响和提出可以有效控制系统运行风险的含风电电力系统优化调度模型。

本文提出将机组投运风险度作为运行可靠性指标计入约束条件。

综合式（2）～式（11）就是本文建立的考虑运行可靠性的含风电电力系统优化调度模型。

由于投运风险度约束是对调度周期内每个时段的机组投运情况进行风险水平的约束，本文提出的考虑运行可靠性的含风电电力系统优化调度模型不仅充分考虑到了风电时序波动的基本特征，可以约束每个时段风电的波动性对系统运行的影响，而且也符合传统的按时段进行机组安排的调度模式。

投运风险度的计算方法[18]简单叙述如下：

（1）得到各机组的停运置换率（Outage Replacement Rate，ORR）

式中，λ是机组的故障率；T是系统的前导时间；停运置换率ORR表示在前导时间T内一台机组故障并且没有得到替代的概率。

（2）建立传统发电系统容量停运概率表。可以采用文献[22]中的方法，建立传统发电系统的容量停运概率表，区别在于要用（1）中得到的机组的停运置换率ORR代替强迫停运率FOR进行计算。由于每个时段机组的投运情况不同，所以每个时段都要形成对应的容量停运表。

（3）建立含风电场的系统容量停运概率表。根据时序多状态风电场风电功率输出模型可以得到每个时段风电场的停运概率见表2，表中Ce为风电场容量。

表2 风电场停运概率表Tab.2 Outage probability of wind farm

将每个时段的风电场停运概率表和传统发电系统的容量停运概率表进行卷积可以得到含风电场的发电系统容量停运概率表。

（4）计算机组投运风险度。每个时段的发电系统容量停运概率表与该时段的负荷模型进行合并，即可得到每个时段的机组投运风险度。

3.4 考虑风电的电力系统优化调度新策略

增加投运风险度约束虽然可以直接有效地控制系统的运行风险，但是目前投运风险度没有一个可以参照的标准，这实际上也限制了它的应用。Billinton.R[12]曾提出将投运风险度设定为 0.001，0.000 1，0.000 01分别表示系统处于高度风险，中度风险和低度风险，但这一划分还是比较粗略，难以在不同的实际系统中应用。而一个可接受的风险水平，必须要根据经济和社会的需求来决定。为摆脱当前国内外还没有运行可靠性标准对运行可靠性实际应用的限制，本文提出了含风电电力系统优化调度新策略，即以不含风电时系统优化调度方案中最大的投运风险度值作为含风电时投运风险度的上限值。

具体过程是设UCRNWt为不含风电的电力系统优化调度中时段t的投运风险度，UCRWt为考虑风电的电力系统优化调度中时段t的投运风险度，ε是一定的裕量值。于是考虑风电的电力系统优化调度投运风险度约束式（11）可以写成

在风电接入系统后，保证任一时段系统的运行可靠性都不低于不含风电时该系统最恶劣的运行情况。由于原来没有运行可靠性的标准，运行人员可能对运行可靠性的指标没有感性认识，但是运行人员对不含风电电力系统运行有丰富的经验。通过对比不含风电与含风电时系统投运风险度指标，运行人员可以理性地判断含风电电力系统时每一时段系统的可靠性，为他们的运行决策提供科学的参考依据。

4 应用混合整数规划算法求解模型

本文运用优化软件Cplex的MIP优化器求解所建立的模型。由于原数学模型是一个非凸高次的MIP模型，无法直接使用Cplex的MIP优化器求解。所以首先要通过数学变换，将模型变为凸二次MIP模型。

4.1 目标函数的变换

一般地，电力系统优化调度模型都有两组控制变量[21]。一组是机组的输出功率；另一组是机组的启停状态。两组控制变量导致模型变得十分复杂。最直接的影响就是目标函数中发电成本部分出现了高次项。本文只将机组的出力变量作为控制变量，而将机组的启停状态变量作为状态变量。为达到这个目的，可以把机组的出力pi定义为半连续变量，即

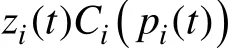
经过以上的数学变换后，最终的目标函数为

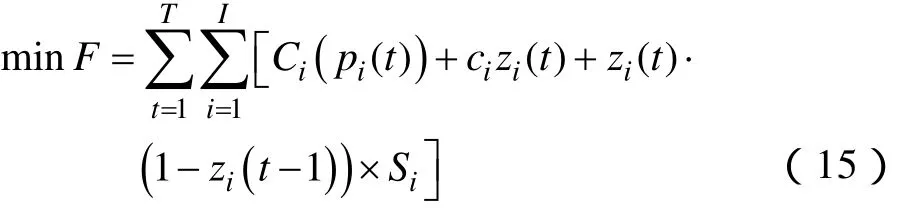
4.2 机组启停约束条件的变换

为此，可以将机组启停约束条件变换为

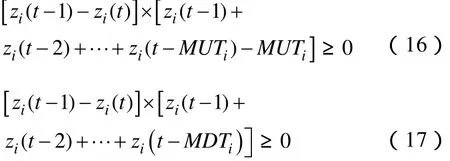
完成对模型的数学变换后，就可以调用Cplex中的MIP优化器对模型进行求解。本文提出的含风电电力系统优化调度模型求解的算法流程如图1所示。

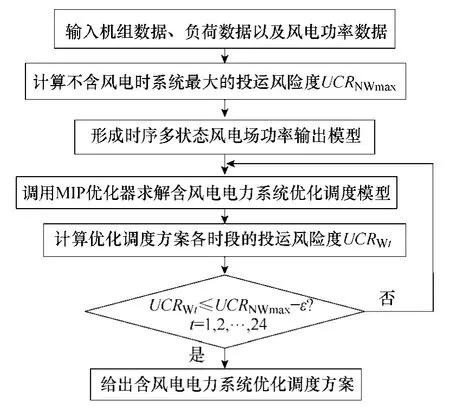
图1 算法流程Fig.1 Flow chart of algorithm

5 算例分析

本文采用的算例是 IEEE RTS-96标准测试系统[22]，该系统中共有32台发电机，总容量为3 405MW。日最大负荷为2 850MW，负荷曲线、每台发电机的物理特性参数和故障概率见文献[22]，每台发电机的运行费用参数a，b，c见文献[25]。风电场总装机容量分200MW、400MW和600MW三种情况进行比较研究。图2给出了风电场总装机容量400MW时风电场日前预测功率曲线。优化调度周期为24h，分为24个时段。系统前导时间设为1h。

图2 风电场输出功率曲线Fig.2 Wind power profile

5.1 时序多状态风电场功率输出模型

本文使用的是以10min为间隔的风电功率预测数据。每小时6个风电数据。使用第2节中提出的方法，以风电场容量为 400MW为例，形成的时序多状态风电场功率输出模型见表 3（限于篇幅，仅列举了前4个时段的情况）。按照表2所示的方法，可以由时序多状态风电场功率输出模型得到每个时段风电场的停运概率表。

表3 时序多状态风电场功率输出模型Tab.3 Time sequential multi-state wind farm power output model

5.2 不考虑投运风险度约束的含风电的电力系统优化调度

风电并网一方面使得系统的运行费用降低，如图3所示；另一方面，也使得系统的运行可靠性下降，投运风险度指标急剧恶化，如图4所示。纵坐标投运风险度指标以lg对数形式给出。从图4可以看出，风电装机容量200MW、400MW、600MW，分别有4个时段、8个时段、10个时段的投运风险度高于不含风电时最高的投运风险度指标。注意，由于优化调度模型中有机组最小启停时间的约束，所以可能会出现某些时段风电装机容量增大，系统投运风险度越低的现象，这也正是分析含风电系统优化调度复杂之处。对于含风电电力系统优化调度，确实是有必要引入投运风险度约束，来降低系统的运行风险，提高系统的可靠性。

图3 不考虑投运风险度约束时系统的运行费用优化结果Fig.3 Optimal results not considering UCR constrains

图4 不考虑投运风险度约束时各时段系统投运风险度指标Fig.4 Hourly UCR index not considering UCR constrains

5.3 考虑投运风险度含风电电力系统优化调度和优化调度新策略

不含风电时，本文算例的优化调度方案的最大投运风险度值为 3.07×10-5。根据本文提出的优化调度新策略，将含风电电力系统优化调度的投运风险度上限值设为3×10-5。此时，系统总运行费用如图 5所示。风电装机容量为 200MW、400MW、600MW时，为了满足运行可靠性的约束，系统增加的运行费用分别为1 927$、2 957$和3 456$。

图5 系统总运行费用的优化结果比较Fig.5 Comparison of optimization results considering UCR constrains or not

图6给出了考虑投运风险度约束后，系统每个时段的投运风险度。此时，含风电系统任一时段的投运风险度指标都低于不含风电时最高的投运风险度指标，确保了含风电系统的运行可靠性。从运行可靠性的角度看，此时的系统运行状态与不含风电时的系统运行状态具有可比性，这样可以为调度人员进行含风电系统的调度运行提供科学的判断依据。

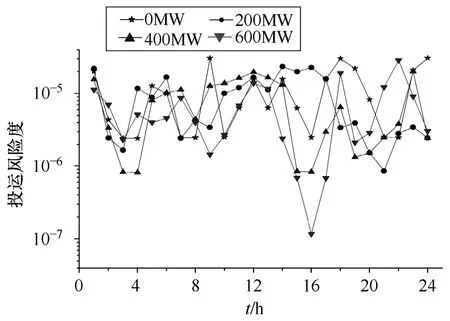
图6 考虑投运风险度约束时各时段系统投运风险度指标Fig.6 Hourly UCR index considering UCR constrains

图7给出了本文提出的优化调度新策略下，风电装机容量为 400MW 时系统的优化调度方案。其中有6台水电机组，本文认为水电处于丰水期，水电满发，故没有在图中给出。

图7 风电装机容量400MW时机组优化出力情况Fig.7 Optimal solution with 400MW wind power capacity

算例结果表明了本文提出的优化调度新策略和求解算法的有效性和实用性，而且能较好地分析风电对电力系统优化调度的影响，为调度方式的安排提供切实可行的参考。

6 结论

从以上讨论，可得出以下结论：

（1）本文建立了时序多状态风电功率输出模型，较好地反映了风电功率的时序性和波动性的特征，适合含风电的电力系统优化调度研究。

（2）风电并网运行会对传统机组产生“替代效应”，从运行可靠性的角度分析，“替代效应”的负面影响是会导致系统的投运风险度水平上升，随着风电并网容量的增加，系统的运行风险显著增大，所以增加投运风险度约束对于含风电电力系统优化调度非常必要。

（3）提出了考虑投运风险度约束的含风电电力系统优化调度模型，该模型能很好地应对风电并网带来的负面影响，并采用基于优化软件Cplex的求解算法，算例结果显示了模型和算法的有效性和实用性。

（4）本文提出的考虑风电电力系统优化调度新策略，突破了当前国内外还没有运行可靠性标准对运行可靠性实际应用的局限，可以实现从不含风电系统的调度模式向含风电系统的调度模式的平稳和安全的过渡，降低系统的运行风险,使含风电电力系统可靠、安全、经济的运行，同时也为调度人员进行含风电系统的调度运行提供科学的判断依据。

[1] Chen C L. Optimal wind-thermal generating unit commitment[J]. IEEE Transactions on Energy Conversion, 2008, 23 (1): 273-280.

[2] Lee T Y. Optimal spinning reserve for a wind-thermal power system using EIPSO[J]. IEEE Transactions on Power Systems, 2007, 22 (4):1612-1621.

[3] 栾士岩, 蒋传文, 张焰, 等. 含风电厂的电力系统节能减排优化调度研究[J]. 华东电力, 2010, 38 (1):39-43.Luan Shiyan, Jiang Chuanwen, Zhang Yan, et al.Research on optimization dispatching for saving energy and reducing emissions in wind power integrated power system[J]. East China Electric Power, 2010, 38(1): 39-43.

[4] 周玮, 彭昱, 孙辉, 等. 含风电场的电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(25): 13-18.Zhou Wei, Peng Yu, Sun Hui, et al. Dynamic economic dispatch in wind power integrated system[J].Proceedings of the CSEE, 2009, 29(25): 13-18.

[5] Tuohy A, Meibom P, Denny E, et al. Unit commitment for systems with significant wind penetration[J].IEEE Transactions on Power Systems, 2009, 24 (2):592-601.

[6] Pappala V S, Erlich I, Singh S N. Unit commitment under wind power and demand uncertainties[C]. Joint International Conference on Power System Technology and IEEE Power India Conference, New Delhi(India), 2008: 1-6.

[7] 江岳文, 陈冲, 温步瀛. 含风电场的电力系统机组组合问题随机模拟粒子群算法[J]. 电工技术学报,2009, 24 (6): 129-137.Jiang Yuewen, Chen Chong, Wen Buying. Partical swarm research of stochastic simulation for unit commitment in wind farms integrated power system[J]. Transactions of China Electrotechnical Society,2009, 24(6): 129-137.

[8] Venkatesh B, Yu P, H B Gooi, et al. Fuzzy MILP unit commitment incorporating wind generators[J]. IEEE Transactions on Power System, 2008, 23 (4): 1738-1746.

[9] 杨梓俊, 丁明, 孙昕. 电力市场下综合考虑系统可靠性和旋转备用效益的机组组合[J]. 电网技术,2003, 27(6): 13-18.Yang Zijun, Ding Ming, Sun Xin. Unit commitment problem under the condition of electricity market considering system reliability and benefit from spinning reserve[J]. Power System Technology, 2003,27(6): 13-18.

[10] 孟祥星, 王宏. 大规模风电并网条件下的电力系统调度[J]. 东北电力大学学报, 2009, 29 (1): 1-7.Meng Xiangxin,Wang Hong.Electric system scheduling in the condition of synchronization of large-scale wind power[J]. Journal of Northeast Dianli University Natural Science Edition, 2009, 29(1): 1-7.

[11] Billinton R, Karki B, Karki R, et al. Unit commitment risk analysis of wind integrated power systems[J].IEEE Transactions on Power System, 2009, 24 (2):930-939.

[12] Xifan Wang, Huizhu Dai, R J Thomas. Reliability modeling of large wind farms and associated electric utility interface systems[J]. IEEE Transactions on Power Apparatus and System, 1984, 103 (3): 569-575.

[13] 张节潭, 程浩忠, 胡泽春, 等. 含风电场的电力系统随机生产模拟[J]. 中国电机工程学报, 2009, 29(28): 34-39.Zhang Jietan, Cheng Haozhong, Hu Zechun, et al.Power system probabilistic production simulation including wind farms[J]. Proceedings of the CSEE,2009, 29(28): 34-39.

[14] A A Chowdhury. Reliability models for large wind farms in generation system planning[C]. IEEE Power Engineering Society General Meeting, Denver(America), 2005: 1926-1933.

[15] Zhaohong Bie, Xin Zou, Zijing Wang, et al. Studies on models and algorithms of the power system probabilistic production simulation integrated with wind farm[C]. IEEE Power and Energy Society General Meeting, Calgary(Canada), 2009: 1-7.

[16] Ensslin C, Milligan M, Holttinen H, et al. Current methods to calculate capacity credit of wind power[C]. IEEE Power and Energy Society General Meeting，Pittsburgh(America), 2008: 1-3.

[17] 王德生, 胡小正. 电力系统运行可靠性评估[J]. 电网技术, 1988, 6(3): 41-46.Wang Desheng, Hu Xiaozheng. Power system operation reliability evaluation[J]. Power System Technology, 1988, 6(3): 41-46.

[18] 周家启, 任震. 电力系统可靠性评估[M]. 重庆: 科学技术文献出版社重庆分社, 1986.

[19] 杨莳百, 丁明. 大型电力系统可靠性技术(四)[J].电力系统自动化, 1994, 18(1): 58-62.Yang Shibai, Ding Ming. Bulk power system reliability evaluation technology(4)[J]. Automation of Electic Power Systems, 1994, 18(1): 58-62.

[20] 王锡凡. 电力系统优化规划[M]. 北京: 水利水电出版社, 1990.

[21] 陈皓勇, 王锡凡. 机组组合问题的优化方法综述[J].电力系统自动化, 1999, 23 (4): 51-56.Chen Haoyong, Wang Xifan.A survey of optimizationbased methods for unit commitment[J]. Automation of Electic Power Systems, 1999, 23(4): 51-56.

[22] IEEE RTS Task Force of APM Subcommittee. The IEEE reliabolity test system-1996[J]. IEEE Transactions on Power Systems, 1999, 14(3): 1010-1020.

[23] Gaing Z L. Discrete partical swarm optimization algorithm for unit commitment[C]. IEEE Power Engineering Society General Meeting, Taiwan(China),2003: 418-424.