基于共轭-旋转矢量不变性技术的谐波检测方法

程志友 程 晨 付学敏 王家琦

（1. 教育部电能质量工程研究中心 合肥 230601 2. 安徽大学电子信息工程学院 合肥 230601）

1 引言

随着工业自动化生产水平的提高，电网中大量应用非线性用电负荷，使谐波污染日益复杂化[1,2]。由于谐波对电力系统和用电设备运行的安全性、稳定性、可靠性和经济性造成很大的影响，因此有必要结合新的工具快速、准确检测电力系统中的谐波，为谐波分析和治理提供可靠保证。

传统的电力系统谐波检测方法最常用的是基于快速傅里叶变换（FFT）[3]，但由于频谱泄露和栅栏效应，容易丢失一些谐波信息，并产生一些虚假的间谐波信号。文献[4,5]采用连续小波变换来检测，由于尺度不同容易引起频域内互相干扰，易受噪声影响。连续小波变换和傅里叶变换相结合的方法能检测出非整数次谐波，但是无法分离相差不大的间谐波。多重信号分类（Multi-Signal Classification，MUSIC）算法[6]可以准确检测出谐波，但计算量大，需要进行峰值搜索，在峰值搜索过程中也有类似栅栏效应，致使频率检测精度仍不够理想。传统的子空间旋转不变性（Estimating Signal Parameters Via Rotational Invariance Techniques，ESPRIT）算法无须进行谱峰搜索，大大降低了计算复杂度，但未对信号子空间进行处理，在噪声较大的情况下精确度不高。最小二乘-子空间旋转不变性（TLS-ESPRIT）算法[7]采用了一种总体最小二乘法的思想减小信号子空间中噪声的干扰，可以得到准确的谐波参数，但需要将样本数据根据快拍数进行划分，使样本数据矩阵维数降低，不能达到最优化估计。

共轭-旋转矢量不变性技术（Conjugate Signal Parameters via Rotational Invariance Techniques,C-SPRIT）算法结合总体最小二乘法抗噪性强的优点，首先根据样本数据构造大小与样本数据数目相等的子阵列，然后奇异值分解子阵列构成的数据矩阵，利用旋转因子共轭矩阵代替旋转因子计算谐波频率值，最后采用 Prony方法[8]中的最小二乘法得到幅值。

2 基于C-SPRIT算法谐波检测方法原理

2.1 抽样信号模型

假设一个信号由P个谐波信号和一个高斯白噪声信号组成[9]，采样信号为

2.2 C-SPRIT算法原理

已有样本数据构造阵列X1(t)，然后构造另一组阵列X2(t)，两阵列构成与对应关系如图1所示[10]。

图1 子阵列构造Fig.1 The structure of sub-arrays

阵列1与阵列2完全重叠，重叠数目为最大值M，两阵列元素的排列顺序不同，∗为共轭。图中，

2.3 总体最小二乘法原理

3 C-SPRIT算法实现过程

4 仿真实验

仿真信号设为

δ(t) 为高斯白噪声，信噪比SNR=30dB，采样频率为1 280Hz，连续取511个数据，仿真信号中含有基波信号和多次谐波间谐波信号，谐波频率为250Hz和 350Hz，对应幅值分别为 0.1(pu) 和 0.032(pu)。有 30Hz和 170Hz间谐波，幅值分别为 0.04(pu) 和0.05(pu)，基波幅值为1。信号添加高斯白噪声之后的波形图如图2所示，波形时间为0～0.2s。

通过C-SPRIT算法谐波信号中基波信号和各次谐波信号均精确的提取出来，基波信号频率估计值为50.00Hz，幅值为1.000 7(pu)。30Hz间谐波信号估计值为 30.02Hz；170Hz间谐波频率估计值为170.01Hz；250Hz谐波频率估计值为 250.00Hz；350Hz谐波频率估计值为350.02Hz。各次谐波幅值估计值分别为 0.039 1(pu)(30Hz)、0.050 7(pu)(170Hz)、0.099 4(pu)(250Hz) 和 0.031 5(pu)(350Hz)，实验结果如图3所示。

图3 C-SPRTI频率检测结果Fig.3 Frequencies estimated results via C-SPRIT

4.1 对比实验1

定义参数误差公式

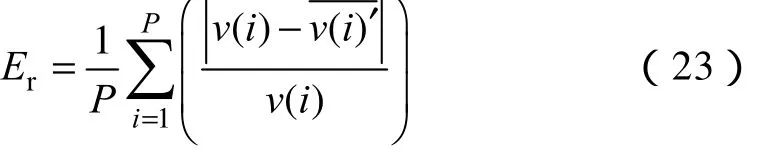
式中，(i) 为基波或谐波频率与幅值的初始值；为多次测量取的平均值。通过仿真实验，比较本文算法与FFT算法，分别计算频率、幅值误差。实验结果见表 1，C-SPRIT算法频率误差为 0.018 2%，幅值误差为 1.16%。FFT算法频率误差为 0.31%，幅值误差为 13.72%，由于 FFT算法会造成频谱泄露，因此会带来较大的误差。分析表明，本文算法比FFT算法频率、幅值估计精确度更高。

表1 C-SPRIT与FFT比较Tab.1 Comparison between C-SPRIT and FFT

4.2 对比试验2

为了进一步验证算法的精确性，取实验1中的相同的 511个样本数据点，分别利用 C-SPRIT、LS-ESPRIT（最小二乘-空间旋转不变性）、TLS-ESPRIT（总体最小二乘-空间旋转不变性）和TAM 算法[15]（Toeplitz近似法）提取谐波参数，LS-ESPRIT、TLS-ESPRIT[16,17]和TAM算法是空间谱算法中应用较多的三类算法，精确度较高。得到实验结果如表2所示。

表2 C-SPRIT与LS、TLS、TAM比较Tab.2 Comparison between C-SPRIT and LS-,TLS-,TAM

由表 2知，利用相同的样本数据，在信噪比SNR=30dB的条件下，C-SPRIT算法频率估计误差为0.018 2%，幅值估计误差为1.16%，均小于其他三类算法的估计结果，因此C-SPRIT算法频率值频率与幅值估计结果更精确。在不同的信噪比环境下，分别利用以上四类算法对相同的样本数据估计频率幅值，图4为频率误差、幅值误差与信噪比关系，在不同的信噪比环境下，TLS-ESPRIT、LS-ESPRIT和 TAM 算法的频率估计值相差不大，随着信噪比降低，估计精度下降，SNR=15dB时，误差值增大到 0.41%。C-SPRIT估计误差小于前三种算法，因此抗噪能力强，SNR=15dB时，误差值为 0.08%。C-SPRIT算法估计的幅值误差小于其他三种算法，信噪比较高时，TLS与TAM估计结果优于LS算法。由此可得，C-SPRIT较 TLS-ESPRIT、LS-ESPRIT和 TAM 算法有更好的抗干扰性，在低信噪比的环境下，仍可以精确的估计出频率与幅值。

图4 不同信噪比下效果比较Fig.4 Comparison between the effect in different SNRS

5 实际数据分析

从某一炼钢厂电弧炉某一相取出一段电流数据，利用C-SPRIT算法对采样数据进行分析。图5为实时信号波形图。采样频率为 6 400Hz，可以看出该电流信号含有大量谐波。图6为利用C-SPRIT算法分析得到的实时信号幅频特性图。

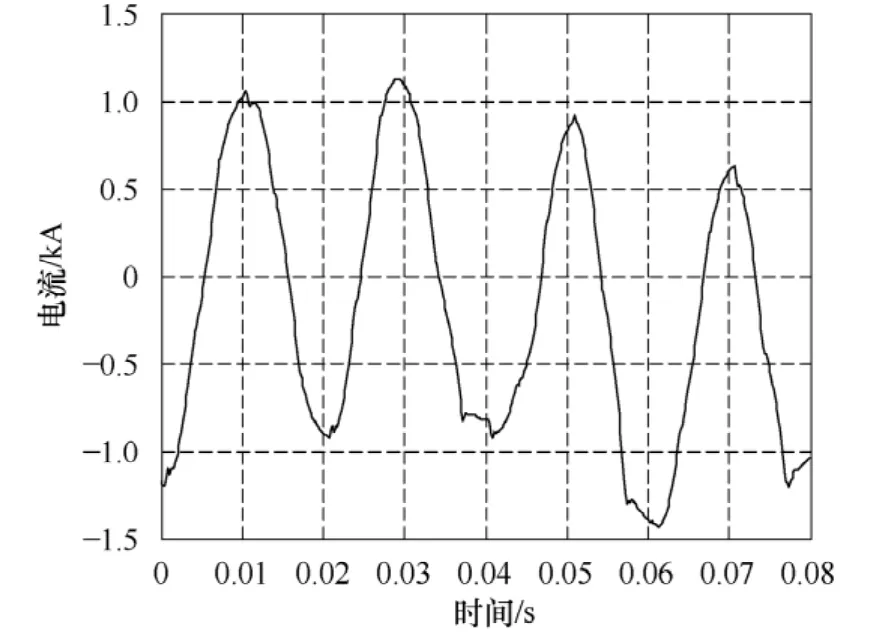
图5 实时信号波形Fig.5 Waveforms of real-time signal

图6 C-SPRIT算法检测的频率检测结果Fig.6 Frequency estimated results via C-SPRIT

在计算机处理器为Pentium（R）Dual-Core CPU E5800@3.20GHz；内存为 1.99GB；操作系统为 32位 Win7；MATLAB 7.0版本下，该算法的用时为14.1ms，通过C-SPRIT算法可以将基波和各次谐波间谐波信号提取出来（幅值小于0.01kA忽略不计），频率大小为 49.98Hz、10.76Hz、27.31Hz、73.76Hz、90.90Hz、110.01Hz、244.80Hz、252.26Hz和350.54Hz。幅值分别为 0.488 3kA、0.154 1kA、0.040 2kA、0.113 9kA、0.096 3kA、0.036 9kA、0.011 2kA、0.014 6kA和0.010 7kA。实验结果表明该算法可以处理实时数据，具有一定的可应用性。

6 结论

（1）本文将 C-SPRIT算法应用于电力谐波检测，该算法在样本数据较少的情况下能够精确地估计出各次谐波、间谐波的频率与幅值信息。

（2）仿真实验表明，该方法优于FFT方法和其他几种常用的空间谱频率检测算法。

（3）实时数据分析表明，该算法可以在实时信号处理中得到应用，因此C-SPRIT是一种精确有效的谐波、间谐波检测方法，可以为谐波间谐波分析提供一种新的工具。

[1] 林海雪. 电力系统中的间谐波问题[J]. 供用电,2001, 18(3): 6-9.Lin Haixue. Interharmonics in electrical power system[J]. Electric Power Research Institute, 2001,18(3): 6-9.

[2] 王兆安, 杨君, 等. 谐波抑制和无功补偿[M]. 北京:机械工业出版社, 2005.

[3] Ferrero A. High accuracy Fouier analysis based on synchronous sampling techniques[J]. IEEE Transmission on Instrument and Measucement, 1992, 41(6): 780-785.

[4] Keaochantanond T, Boonseng C. Harmonics and inter-harmonics estimation using wavelet transform[C].Proceedings of the IEEE Transmission and Distribution Conference and Exhibition, 2002, 2: 775-779.

[5] 周林, 夏雪, 万蕴杰, 等. 基于小波变换的谐波测量方法综述[J]. 电工技术学报, 2006, 21(9): 67-73.Zhou Lin, Xia Xue, Wan Yunjie, et al. Harmonic detection based on wavelet transform[J]. Transactions of China Electrotechnical Society, 2006, 21(9): 67-73.

[6] 蔡涛, 段善旭, 刘方锐. 基于实值MUSIC算法的电力谐波分析[J]. 电工技术学报, 2009, 24(12): 149-155.Cai Tao, Duan Shanxu, Liu Fangrui. Power harmonic analysis based on real-valued spectral MUSIC algorithm[J]. Transactions of China Electrotechnical Society, 2009, 24(12): 149-155.

[7] 聂永辉, 刘彦臣, 张立艳. TLS-ESPRIT技术在电力系统谐波检测的应用[J]. 电力系统及其自动化学报,2010, 22(2): 129-132.Nie Yonghun, Liu Yanchen, Zhang Liyan. Application of TLS-ESPRIT on harmonic measurement of power system[J]. Proceedings of the CSU-EPSA, 2010,22(2): 129-132.

[8] 石敏, 吴正国, 尹为民. 基于多信号分类法和普罗尼法的间谐波参数估计[J]. 电网技术, 2005, 29(15):81-84.Shi Min, Wu Zhengguo, Yin Weimin. Inter-harmonic parameter estimation based on multi-signal classification and prony method[J]. Power System Technology,2005, 29(15): 81-84.

[9] Tayem N, Kwon H M. Conjugate ESPRIT(C-SPRIT)[J]. IEEE Transactions on Antennas and Propagation, 2004, 52(10): 2618-2624.

[10] Delmas J P. Comments on conjugate ESPRIT (CSPRIT)[J]. IEEE Transactions on Antennas Propagation,2007, 55: 511.

[11] 王永良, 陈辉, 彭应宁, 等. 空间谱估计理论与算法[M]. 北京: 清华大学出版社, 2004.

[12] Kung S Y, Arun K S, Rao D V B. State space and SVD based approximation methods for the harmonic retrieval problem[J]. Journal of the Optical Society of America, 1983, 73(12): 1800-1803.

[13] 周云钟, 陈天麒. 一种自适应 ESPRIT算法[J]. 系统工程与电子技术, 2001, 23(9): 5-8, 11.Zhou Yunzhong, Chen Tianqi. An adaptive ESPRIT algorithm[J]. Systems Engineering and Electronics,2001, 23(9): 5-8, 11.

[14] Wax Mati, Kailath Thomas. Detection of signals by information theoretic criteria[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1985,33(2): 387-392.

[15] A study on the application of Toeplitz approximation method on DOA estimation[C]. Proceedings of the 2010 2nd International Conference on Signal Processing Systems(ICSPS), 2010, 3: 215-218.

[16] 张君俊, 杨洪耕. 间谐波参数估计的 TLS-ESPRIT算法[J]. 电力系统及其自动化学报, 2010, 22(2):70-74.Zhang Junjun, Yang Honggeng. TLS-ESPRIT for interharmonic estimation[J]. Proceedings of the CSU-EPSA, 2010, 22(2): 70-74.

[17] 初宪武. 基于TLS-ESPRIT算法和自适应神经网络的间谐波分析[J]. 电工电能新技术, 2010, 29(2): 17-20.Chu Xianwu, Interharmonic analysis based on TLSESPRIT algorithm and adaline neural network[J].Advanced Technology of Electrical Engineering and Energy, 2010, 29(2): 17-20.