规模化EV充电与风力/火电发电系统协调运行

刘文霞 赵天阳 邱 威 张建华

（1.新能源电力系统国家重点实验室（华北电力大学） 北京 102206 2.国家电力调度控制中心 北京 100031）

1 引言

为实现节能减排和清洁能源利用，国家出台了两个重大举措，一是大幅提高风能和太阳能等绿色能源在能源结构中的比重；另一个是大力发展电动汽车，减少对化石燃料的需求。随着并网风电容量的增加，系统调峰能力不足成为限制风电出力的主要因素[1-3]。目前，提高风电并网能力的策略多集中于电源侧，如将风电与火电、水电等常规能源捆绑上网，以平稳发电出力[3]，但未涉及负荷侧的控制。

相比风电的随机性，EV充电负荷的可控性为风电消纳提供了契机。在 EV大规模应用时，系统中将出现EV用户和EV运营商2类新主体[4]。目前针对EV充电的优化研究多集中于电网、EV运营商和EV用户三方面：

在电网侧，文献[5, 6]分别通过集中、分散的控制方式，对 EV充电、家庭用电进行直接控制，实现系统负荷特性的优化和峰谷差的减小；文献[7]在某地区对多个充电点进行日前负荷预分配，并通过多个站点之间实时负荷分配控制，实现系统整体运行费用的优化；文献[8]确立了负荷转移、频率控制与 EV充电负荷关系的模型，通过运营商集中控制EV的充电过程，实现负荷转移与频率控制。

针对EV运营商，文献[9, 10]中由EV运营商完成用户的电能补给，实现运营费用最小或利益最大。上述文献中涉及的电价政策均为实时电价；相比实时电价，分时电价在我国更具有适用性，将在智能电网负荷侧管理中扮演重要角色[11]。

以上研究[5-10]中的控制策略都以满足 EV用户的充电需求为前提，但都未涉及用户的经济性：文献[11]中结合分时电价、电池荷电状态与充电功率的关系，优化充电过程，在降低用户充电费用的同时实现了负荷转移；文献[12]以火电和新能源的差异电价为基础，以用户充电费用最小为目标、用户充电行为调整为手段，在实现充电费用优化的基础上分析了EV充电对电网消纳新能源的影响。

结合目前EV的发展趋势，EV的电能补给主要由电网提供。因此，分析 EV充电对系统运行的影响应主要考虑EV用户和电网两方面的协调。

综合以上研究，本文建立了两阶段的优化策略，如图1所示，以确定规模化EV充电与风力/火电发电系统协调运行机制：第一阶段，在负荷侧，以优化用户充电费用为目标，结合分时电价和充电协议，通过充电过程的优化，获得智能充电方式下的 EV充电负荷；第二阶段，在电网侧，建立了以低发电成本、低污染和低弃风量为目标的多目标动态清洁调度模型，采用了基于MODE[13]的改进微分进化算法（Enhanced Multi-Objective Differential Evolution，EMODE）对模型进行求解，以确定规模化EV充电与风力/火电发电系统协调运行机制，并分析了 EV规模和备用对系统运行的影响。

图1 研究框架Fig.1 Research framework

2 电动汽车充电负荷模型

EV充电负荷是用户充电需求的电能反映，体现于充电设施处，如图2所示。因此，影响EV充电负荷的因素包含用户的行为特性和 EV的充电特性。用户的行为特性包含：日行驶里程dis、充电起始时间ton；EV的充电特性包含EV的充放电特性、充电功率pc[14]。控制用户充电行为时，须满足用户设定的停止充电时间toff[9]。

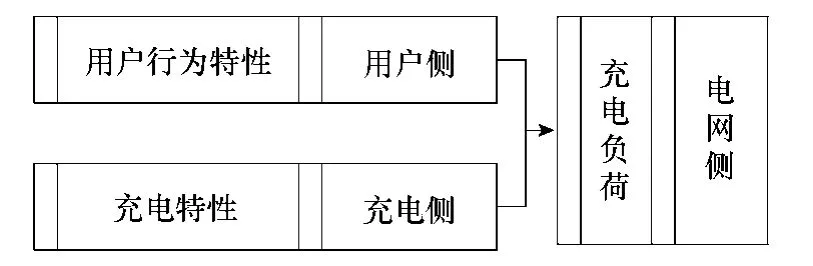
图2 EV充电负荷形成过程Fig.2 Formation of EV charging load

2.1 用户侧

针对用户的行为特性，文献[7, 9]中将燃油车用户的行为特性映射至 EV用户；同时，因不同用途EV的行驶规律差异较大，文献[15]中依据EV的用途对用户进行归类处理，并研究各类用户的行为特性。为便于分析，本文将 EV分为公务、商务和私人3种，具体参数假设见附表1。

用户的充电电量需求与用户上次充电后的行驶里程有直接关系[16]，即

式中，Prequire,i为EVi的充电电量需求；αi为上次充电至此次充电的天数，记为充电天系数；dis,i为用户i的日行驶里程；pd,i为EVi的单位里程耗电量；η为充电效率。

2.2 充电侧

目前，动力电池多采用恒流-恒压的2阶段方式进行充电，充电过程中充电机直流侧功率近似恒定。《电动汽车传导式接口》规定不同充电地点的充电设施具有差异的额定充电功率，本文根据上述协议确定用户在不同充电设施处的额定充电功率pcmax。

根据控制类型的差异，充电方式可分为非控制充电、延迟充电、填谷充电和智能充电[17]。依据北京地区的负荷峰谷划分[18]，各充电控制方式可具体描述为

（1）非控制充电：用户结束行驶后即进行充电，充电过程持续至满电。

（2）延迟充电：用户在负荷高峰期后开始充电，持续至满电；此种充电行为更符合用户的行为特性，文中假设延迟充电的起始时间为23:00。

（3）填谷充电：峰谷时刻，EV的起始充电时间可被调度，行为具有预见性，在规定的时段内服从相应的分布；为避免因EV大量瞬时接入而形成冲击负荷，EV充电起始时间在0:00～3:00内服从均匀分布。

（4）智能充电：为获得削峰填谷效果，激励用户依照分时电价安排充电，即认为在用户接入电网充电的过程中，用户为获得充电费用最小，调整各充电时段的充电功率。

充电方式与 EV的用途和充电设施直接相关。因公务车和商务车具有相对固定的行为特性，较易控制，且填谷充电可有效减小系统峰谷差，提高设备利用率等优点；所以，本文中公务车和商务车仅进行填谷充电。私人用户在规模较大时，对充电负荷必然产生显著影响。因私人用户在商场充电时间有限，控制难度大，因此不对其进行控制；只针对私人用户在家庭充电和办公地点的充电进行优化。为便于分析，构建了4种情景，见表1。

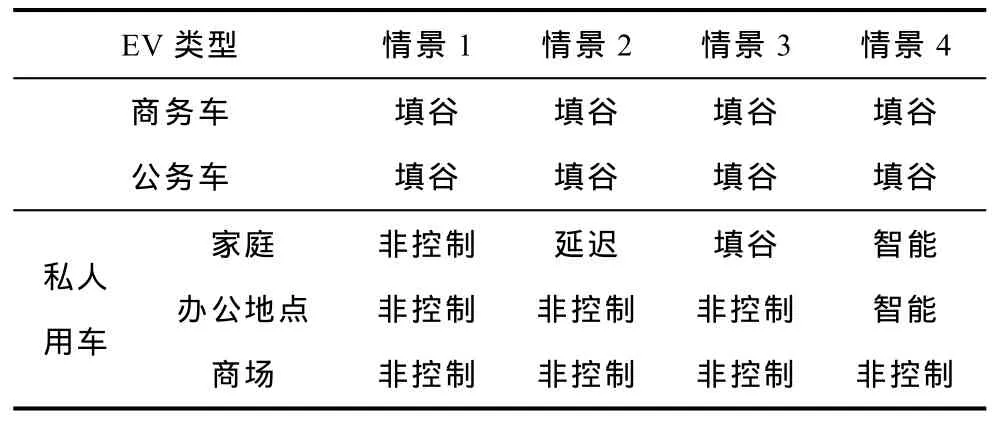
表1 各情景下用户充电安排Tab.1 Charging arrangements for different users in the various scenarios

2.3 电网侧

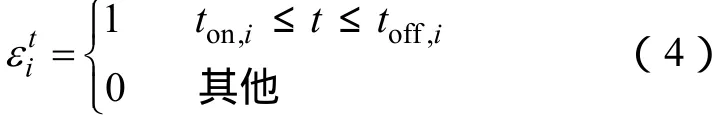
在给定的充电方式下，结合用户的行为特性，根据式（1）～式（4），即可获得由于EV充电产生的充电负荷。由于 EV数量巨大，为便于控制，需对不同类型EV用户按照行为特性进行归类处理。

本文采用蒙特卡洛抽样生成用户行为特性和充电需求后，以ton、toff和Prequire为分类指标，采用k-均值法对其进行归类，获得每类 EV的聚类中心及其包含EV数量，结合表1中的各类型EV的充电方式，从而获得最终充电负荷。

3 多目标清洁调度模型

根据场景分析，得到第一阶段优化后的 EV充电负荷。在给定 EV充电负荷和地区负荷时，考虑调峰裕度，优先满足风电并网。因风电的消纳能力由系统的负调峰能力决定[1]，与火电机组的出力直接相关；且火电机组出力的变动将引起机组发电成本和污染物排放的变化；因此，在满足系统安全稳定的基础上，可通过优化火电机组的出力，以降低系统的发电成本、污染物排放量和弃风量。

目标函数1：系统发电成本最小

（4）系统备用约束：因风电波动和负荷随机性而引起系统负备用的极限情况已在目标函数3中阐述，故在此仅考虑系统的正备用约束。

4 改进多目标微分进化算法

（1）种群初始化。初始种群的多样性和在搜索空间中的分布，对进化算法的优化效果会产生较大的影响，通过将连续空间向量化，正交设计可用于连续空间中的初始种群生成[21]。本文采用文献[21]中提出的正交初始化方法以提高初始解的质量，加快算法收敛。

（2）快速非支配排序。由于临时种群的规模经常超出规定的种群规模，需对临时群体执行NSGA-Ⅱ[22]中的分级和拥挤度计算，将超出种群规模的个体删除，即剪切操作，从而维持种群规模恒定；由于 NSGA-Ⅱ中拥挤度计算时采用的是相邻个体在解空间的欧式空间，不能反映真实的拥挤度，本文中采用文献[23]中的拥挤度计算方法。

（3）微分操作。微分操作包含交叉与变异两个步骤[13]。在微分操作中，控制参数的选取会对算法的性能产生重要的影响。通过将控制参数内嵌入个体内，随种群进化而自适应更新，可有效提高算法的数据挖掘能力[24]。

（4）选择操作。在子代个体与父代个体竞争时，通过（2）中的分级和拥挤度计算后，结合 Pareto支配概念，保证算法的收敛性和解分布的均匀性，从而实现种群的更新。

（5）约束实现。因MODE求解的问题为无约束问题，而多目标动态清洁调度模型中含有功率平衡、爬坡约束等众多的等式、不等式约束，所以需对MODE进行扩展：保证算法搜索性能的同时，实现种群中个体的可行化。

求解含约束的优化问题时，多采用罚函数法，通过将违反约束的程度并入目标函数中考虑，实现算法向可行域进化。但惩罚因子难以选取，因此本文采用了文献[25]中的个体修正策略，实现个体的可行化。

5 算例分析

5.1 算例描述

本文采用的 10台火电机组参数及排污特性见文献[18]，日负荷水平、地区电价，见附表2；不计网损。系统总装机容量为2 969MW：其中火电机组为 2 368MW；风电为 600MW，占总装机容量的20.21%。

结合我国电动汽车的发展规划，在2021～2030年私人电动汽车将获得广泛的发展。根据《中国汽车产业报告（2008）》的预测表明，在2030年中国的私家车与公共车辆的数量分别为17 638和1 800万辆，比例近似为 10∶1。因此，本文假设此地区含有私人车辆为10万辆，商务和公务车共1万辆，详见附表1。依据文献[26]中的假设，私人用户在家庭、工作地点和商场充电的比例分别为 0.7∶0.2∶0.1。其他的参数假设见附表1。

由于采用随机抽样的方法获得的风电机组出力不能反映出风电在时序上的联系，且无法体现风电的反调峰特性；因此本文采用国内某装机容量为100MW风电厂的实际出力，将其典型日出力按比例扩展至装机容量为600MW，见附表2。

在负荷侧，结合电动汽车充电负荷模型，各情景下系统中的充电负荷曲线如图3所示。

图3 不同情景下的系统负荷曲线Fig.3 Load curves under different scenarios

其余参数设置为：风电运行费用ωi为20$/MW；风电正备用系数wu%为20%；βlr和βcr初始选为5%和20%。种群规模为60；正交数组中分层数为9，正交指数值为2；最大迭代次数为1 000。

5.2 风电并网运行分析

5.2.1 EV充电方式对系统运行影响

四种情景下获得的Pareto前沿如图4所示。选取最优折中解后，各情景下的最优折中解对比见表2。对上述最优折中解的分析中除考虑各目标函数外，还应考虑弃风时段、弃风时段中的最大弃风量及弃风量占此时段风电出力的最大比例。

通过图4和表2的分析发现，充电方式对系统运行产生了直接影响：随着充电方式的变化，风电的弃风量、系统的发电成本和排污水平发生了显著变化。

图4 各情景下的Pareto前沿Fig.4 Pareto fronts under different scenarios

通过情景2与情景1的对比可知，发电成本、污染物排放和弃风量分别降低：1.32%、0.32%和30.74%，说明仅将私人用户晚间充电行为与负荷高峰错开，即可优化系统运行，显著降低系统的弃风量。

情景3与情景2相比，将私人用户在晚间的充电行为推迟至峰谷时刻，使系统的负荷曲线更平稳，各目标函数分别降低了0.44%、6.95%和30.76%。

情景4与情景3相比，在晚间的充电负荷近似相同，说明通过分时电价引导用户充电可获得与填谷充电一致的效果，获得了近似的弃风量：370.74MW和 347.34MW；但日间的充电行为调整，进一步降低了系统的负荷波动，使系统的发电成本和污染物排放分别降低了0.02%和0.59%。

综上所述，规模化 EV下，对系统运行最好的充电控制方式为：私人用户采用智能充电方式充电，公务、商务车采用填谷充电。

5.2.2 EV规模对系统运行影响

由式（4）可知，EV充电负荷与EV规模有直接关系，因此需分析 EV规模对风电接纳能力的影响。假设各类EV比例恒定，以原定状态下为常态，以 EV规模±10%波动为非常态，在情景 4下分析EV规模对风力/火电发电系统运行的影响。获得的Pareto前沿如图5所示，最优折中解对比见表3。

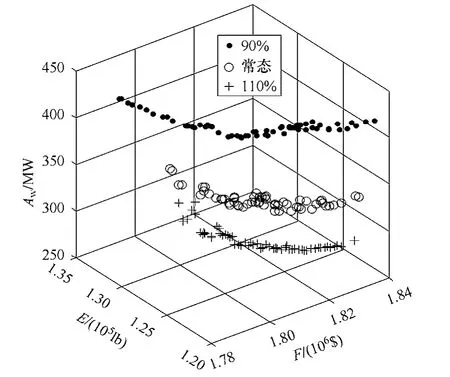
图5 不同EV规模下Pareto前沿Fig.5 Pareto fronts under different EV scales

表2 各情景下的最优折中解对比Tab.2 Comparison of best compromised solutions of different scenarios

表3 各EV规模下的最优折中解对比Tab.3 Comparison of best compromised solutions of different EV scales

通过图5和表3可知，随着EV规模的增加，负荷增加，弃风量显著减小，限风时段和最大限风比例也显著减低，使得系统的污染物排放水平降低；但由于随着负荷的增长，火电机组出力上升，使得系统的发电成本显著增长，由1 799 151.67$上升至1 801 800.28$。

5.2.3 备用对系统运行影响

在式（13）中，因 EV负荷的随机性，系统中需留有一定的负备用。若提高 EV充电负荷的预测精度，会对风电的接纳能力产生正面的影响。为确定 EV充电负荷备用系数对风电接纳能力的影响，文中分别取βcr为20%、15%、10%和5%，在情景4下，各备用系数下的Pareto前沿如图6所示，最优折中解见表4。

各备用系数下的最优折中解见表 4。通过表 4中最优折中解的分析可知，随着βcr的降低：系统的弃风量由347.34MW下降至284.84MW，系统的排污量由126 540.51 lb下降至120 747.81 lb；但随着火电机组出力的逐渐减小，其运行偏离经济性的最优点，使系统的发电成本先降低后升高。

图6 各备用系数下的Pareto前沿Fig.6 Pareto fronts under different reserve coefficients

表4 各备用系数下的最优折中解对比Tab.4 Comparison of best compromised solutions of different reserve coefficients

6 结论

（1）本文首先建立了针对不同用户的差异充电策略，以优化 EV用户充电，并形成不同的充电情景，明确了EV充电负荷对系统负荷的影响；随后，在考虑火电机组负调峰和备用需求的前提下，建立了以系统发电低成本、低污染和风电弃风量小为目标的动态清洁调度模型，明确了规模化 EV充电对风力/火电发电系统运行产生影响的机理。

（2）采用改进微分进化算法求解动态清洁调度模型，确定了充电方式、EV规模和EV备用对风电/火力发电系统运行的影响：基于分时电价的智能充电方式对系统运行最好；随着 EV规模的增加，系统的发电成本上升，而污染物排放和弃风量递减；随着 EV备用的减小，系统的污染物排放和弃风量递减，但系统的发电成本先下降后上升。

附 录

附表1 电动汽车类型及参数设置App. Tab.1 Types and parameters of EVs

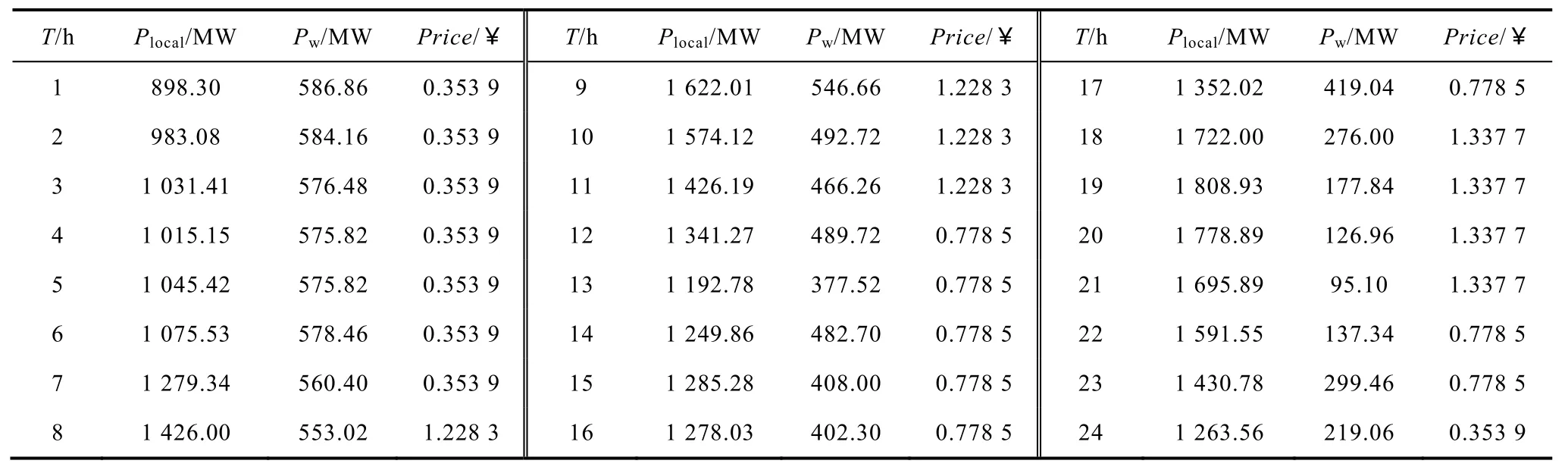
附表2 负荷数据和电价水平App. Tab.2 Load data and price levels

[1] 杨宏, 刘建新, 苑津莎. 风电系统中常规机组负调峰能力研究[J]. 中国电机工程学报, 2010, 30(16):26-31.Yang Hong, Liu Jianxin, Yuan Jinsha. Research of peak load regulation of conventional generators in wind power grid[J]. Proceedings of the CSEE, 2010,30(16): 26-31.

[2] 张宏宇, 印永华, 申洪, 等. 大规模风电接入后的系统调峰充裕性评估[J]. 中国电机工程学报, 2011,31(22): 26-31.Zhang Hongyu, Yin Yonghua, Shen Hong, et al.Peak-load regulating adequacy evaluation associated withlarge-scale wind power integration[J]. Proceedings of the CSEE, 2011, 31(22): 26-31.

[3] 张丽英, 叶廷路, 辛耀中, 等. 大规模风电接入电网的相关问题及措施[J]. 中国电机工程学报, 2010,30(25): 1-9.Zhang Liying, Ye Tinglu, Xin Yaozhong, et al.Problems and measures of power grid accommodating large scale wind power[J]. Proceedings of the CSEE,2010, 30(25): 1-9.

[4] Gomez T, Roman S, Momber I, et al. Regulatory framework and business models for charging plug-in electric vehicles: Infrastructure, agents, and commercial relationships[J]. Energy Policy, 2011, 39: 6360-6375.

[5] Sundström O，Binding C. Flexible charging optimization for electric vehicles considering distribution grid constraints[J]. IEEE Transactions on Smart Grid,2012, 3(1): 26-37.

[6] Shao S N, Pipattanasomporn M，Rahman S. Grid integration of electric vehicles and demand response with customer choice[J]. IEEE Transactions on Smart Grid, 2012, 3(1): 543-550.

[7] Valentine K, G Temple W, Zhang K M. Intelligent electric vehicle charging: Rethinking the valley-fill[J].Journal of Power Sources, 2011(196): 10717-10726.

[8] Ahn C, Li C T, Peng H. Optimal decentralized charging control algorithm for electrified vehicles connected to smart grid[J]. Journal of Power Sources,2011(196): 10369-10379.

[9] Wu D, Aliprantis D C, Ying L. Load scheduling and dispatch for aggregators of plug-in electric vehicles[J].IEEE Transactions on Smart Grid, 2012, 3(1): 368-376.

[10] Kristoffersen T K, Capion K, Meibom P. Optimal charging of electric drive vehicles in a market environment[J]. Applied Energy, 2011, 88: 1940-1948.

[11] Cao Y J, Li C B, Zhang P, et al. An optimized EV charging model considering tou price and soccurve[J].IEEE Transactions on Smart Grid, 2012, 3(1): 388-393.

[12] Pantos M. Stochastic optimal charging of electricdrive vehicles with renewable energy[J]. Energy,2011, 36: 6567-6576.

[13] Robič T, Filipič B. DEMO: differential evolution for multiobjective optimization[C]. Evolutionary Muti-Criterion Optimization 2005, Heidelberg, Germany:Springer, 2005: 520-533.

[14] Darabi Z, Ferdowsi M. Aggregated impact of plug-in hybrid electric vehicles on electricity demand profile[J]. IEEE Transactions on Sustainable Energy, 2011,2(4): 501-508.

[15] 胡泽春, 宋永华, 徐智威, 等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报, 2012, 32(4):1-11.Hu Zechun, Song Yonghua, Xu Zhiwei, et al. Impacts and utilization of electric vehicles integration into power systems[J].Proceedings of the CSEE, 2012,32(4): 1-11.

[16] Qian K J, Zhou C K. Modeling of load demand due to EV battery charging in distribution systems[J]. IEEE Transactions on Power Systems, 2011, 26(2): 802-810.

[17] Peng M H, Liu L, Jiang C W. A review on the economic dispatch and risk management of the large-scale plug-in electric vehicles (PHEVs)-penetrated power systems[J]. Renewable and Sustainable Energy Reviews, 2012, 16: 1508-1515.

[18] Li Z, Ouyang M G. The pricing of charging for electric vehicles in China—Dilemma and solution[J].Energy, 2011, 36: 5765-5778.

[19] Basu M. Dynamic economic emission dispatch using non-dominated sorting genetic algorithm-II[J].International Journal of Electrical Power & Energy Systems, 2008, 30(2): 140-149.

[20] Chen C L, Lee T Y, Jan R M.Optimal wind-thermal coordination dispatch in isolated power systems with large integration of wind capacity[J]. Energy Conversation and Management, 2006, 47: 3456-3472.

[21] Leung Y W, Wang Y P. An orthogonal genetic algorithm with quantization for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2001, 5(1): 41-53.

[22] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation, 2002,6(2): 182-197.

[23] 彭春华, 孙惠娟. 基于非劣排序微分进化的多目标优化发电调度[J]. 中国电机工程学报, 2009, 29(34):71-76.Peng Chunhua, Sun Huijuan. Multi-objective optimization power dispatchbased on non-dominated sorting differential evolution[J]. Proceedings of the CSEE,2009, 29(34): 71-76.

[24] Brest J, Greiner S, Bošković B, et al. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems[J].IEEE Transactions on Evolutionary Computation,2006, 10(6): 646-657.

[25] Lu Y L, Zhou J Z, Qin H, et al. Chaotic differential evolution methods for dynamic economic dispatch with valve-point effects[J]. Engineering Applications of Artificial Intelligence, 2011, 24: 378-387.

[26] Luo Z W, Song Y H, Hu Z C, et al. Forecasting charging load of plug-in electricvehicles in China[C].Power and Energy Society General Meeting, San Diego, CA, 2011.