关于“单纯形法选择进出基变元的一个新准则”的计算效率

高培旺

(闽江学院 数学系，福建 福州 350108)

线性规划广泛应用于经济与管理的各个领域[1-2]，研究大规模线性规划问题的数值方法可以快速准确地为管理者提供决策策略.单纯形法是求解线性规划实际问题非常有效的算法.从理论上看，经典单纯形法通过旋转迭代从可行域的一个顶点到达另一个相邻顶点，直到获得最优解(如果存在).显然，在n(n>2)维空间中，从一个顶点出发，使目标函数值增大(考虑最大化问题)的路径不止一条.为了找到通往最优顶点的最佳路线、减少迭代次数，人们提出了不同的单纯形变式，如梯度单纯形算法[3-4]、原有一对偶单纯算法[5-6]及其他方法.其中，文献[7]提出了单纯形算法的一种改进的枢轴准则，并用一个很小的例子说明了其计算效率优于经典的单纯形算法，既没有给出严密的复杂性分析，也没有进行大规模的数值试验，因而是远远不够的.

本研究对“单纯形法选择进出基变元的一个新准则”进行了分析，详细给出了算法步骤，并通过大规模的数值试验进一步揭示了该算法的计算效率.结果表明，这种改进的单纯形算法虽然在大部分问题上的迭代次数比经典的单纯形算法有所减少，但所耗费的计算时间却大大增加，其计算效率随着问题规模的增大而不断下降.实际上，Arsham[8-9]也提出了与“单纯形法选择进出基变元的一个新准则”类似的算法思想，Enge和Huhn[10]从复杂性理论上指出了这种单纯形枢轴准则的缺陷，即迭代次数的减少一般不能弥补由逐列选择枢轴主元的枢轴准则所带来的计算复杂性.

1 “单纯形法选择进出基变元的一个新准则”的算法思想

考虑如下形式的线性规划问题：

(LP)

maxf=cTx

s.t.Ax=b，x≥0.

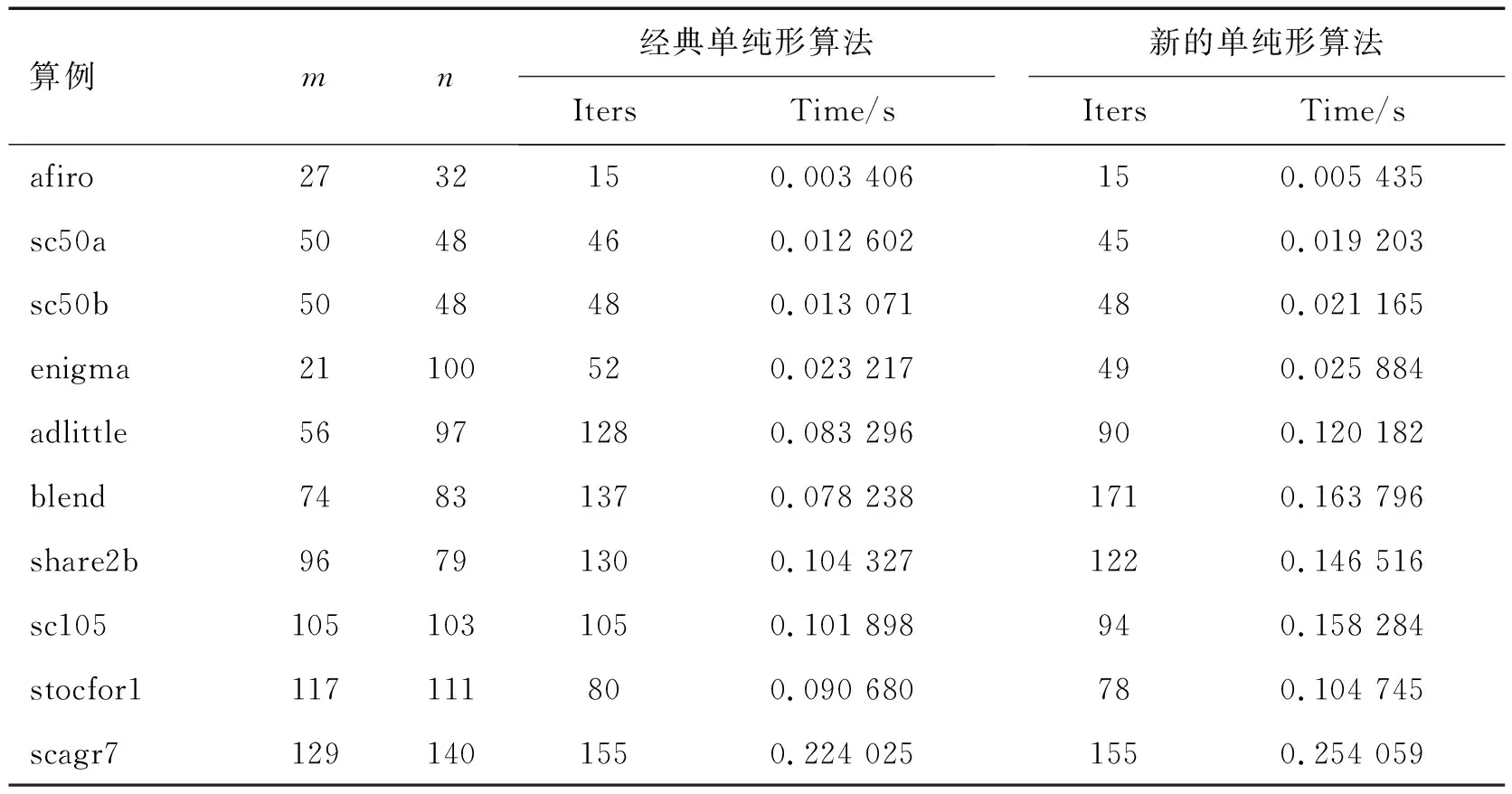
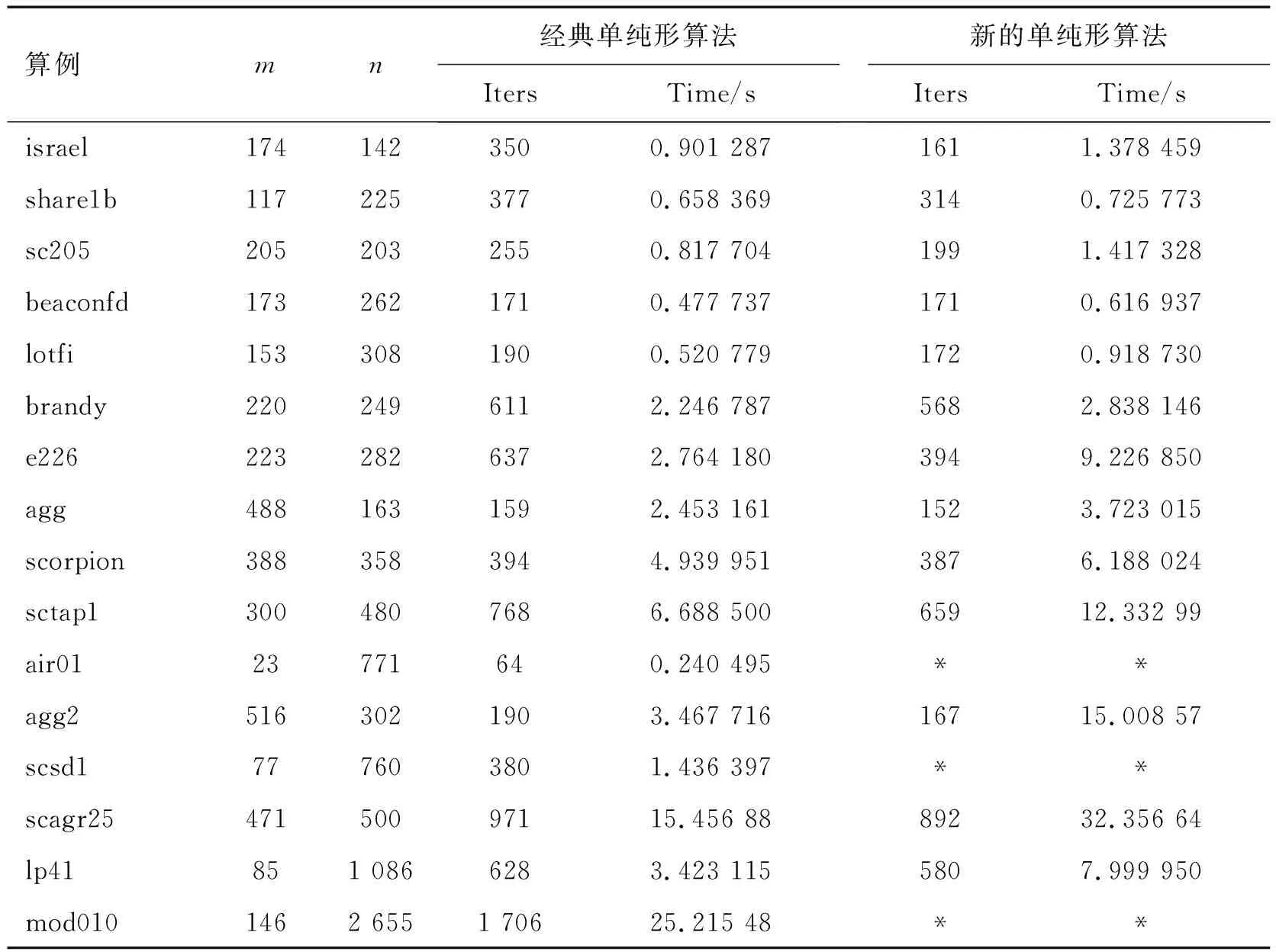
这里，A∈Rm×n(m

f′=f0+θkσl,

(1)

(1)计算判别数σ=c-cBB-1A，如果σ≤0，则当前原有可行解是最优解，算法结束；否则转下一步.

通过执行上述算法步骤，或者获得原问题的一个基本可行解，或者得到问题有无界解的事实.

2 关于“单纯形法选择进出基变元的一个新准则”的计算效率

从理论上看，“单纯形法选择进出基变元的一个新准则”也许会减少单纯形迭代次数，但由于枢轴准则的设计计算更复杂，计算效率是否会提高必须要进行大规模的计算试验和比较.为此，使用Matlab V7.1语言对经典单纯形算法和文献[7]提出的改进单纯形算法进行了编程.在计算机上求解计算了26个大规模典型算例，以比较经典单纯形算法和改进的单纯形算法的计算效率，其中问题adlittle，afiro，agg，agg2，beaconfd，blend，brandy，e226，israel，lotfi，sc105，sc205，sc50a，sc50b，scagr7，scagr25，scorpion，scsd1，sctap1，share1b，share2b和stocfor1来自线性规划数据库NETLIB[11]，问题air01，enigma，lp41，mod010来自混合整数规划数据库MIPLIB[12]，计算结果如表1所示.其中，Iters表示求解线性规划问题所需要的枢轴(迭代)数，Time表示所耗费的总的计算时间.

表1 经典单纯形算法和新的单纯形算法的计算比较Tab.1 Computational comparison for the classical and new simplex algorithms

续表

注：*表示该问题在执行了2 000次单纯形迭代后，仍然没有获得问题的解.

从表1可以看到，除问题blend外，文献[7]提出的新的单纯形枢轴准则一般比经典的单纯形算法所用的迭代次数少，但每一个问题所耗费的计算时间都要比经典的单纯形算法多.尤其是随着问题的决策变量数增多与规模增大，新的单纯形枢轴准则比经典的单纯形算法所用的计算时间更长、计算效率更低.

3 结束语

本研究对文献[7]提出的“单纯形法选择进出基变元的一个新准则”进行了大规模数值试验，以进一步考察这种新的单纯形枢轴准则的计算效率.从理论上看，这种所谓“新”的单纯形枢轴准则能够使目标值在每次单纯形迭代时得到最大增益，从而导致单纯形迭代次数减少.但在实际中，枢轴准则设计计算的复杂性却大大降低了这种算法的计算效率.从问题e226的计算结果中可以看到，这种新的枢轴准则使单纯形迭代次数比经典的单纯形算法减少了接近一半，但计算时间却是经典算法的4倍左右，可谓得不偿失.

另外，文献[7]列举了一个经典单纯形迭代循环的例子来试图说明新的单纯形枢轴准则可以克服因退化产生的迭代循环问题，然而这仅仅是一个个例，在理论上并没有证明.实际上，从表1可以看到，新的单纯形枢轴准则也会产生迭代循环的现象，如问题air01，scsd1和mod010.

通过对“单纯形法选择进出基变元的一个新准则”进行的大规模数值试验可以发现，理论上“最佳”的枢轴准则在实际中不一定是最好的，经典单纯形算法的简单而方便实用的枢轴准尽管“在最坏情况下”的迭代数是指数增长的，但实际使用效果非常好，这已经为很多的实际问题所验证.类似文献[7]的单纯形算法还可找到一些[13].因此，提出一种新且“好”的单纯形枢轴准则并不是一件容易的事情，在进行理论探讨的同时还需要大规模数值试验来验证.

参考文献：

[1] Adlakha V,Kowalski K,Vemuganti R,et al.More-for-less algorithm for fixed-charge transportation problems[J].Omega, 2007，35(1):116-127.

[2] Sonia，Puri M C.Two-stage time minimizing assignment problem[J].Omega，2008，36(5): 730-740.

[3] Forrest J，Goldfarb D.Steepest-edge simplex algorithm for linear programming[J].Mathematical Programming，1992，57(1): 341-374.

[4] Vemuganti R R.On gradient simplex methods for linear programs[J].Journal of Applied Mathematics and Decision Sciences，2004，8(2): 107-129.

[5] Curet N D.A primal-dual simplex method for linear programs[J].Operations Research Letters，1993，13(5): 233-237.

[6] Chen H D，Pardalos P M，Saunders M A.The simplex algorithm with a new primal and dual pivot rule[J].Operations Research Letters，1994，16(3): 121-127.

[7] 王全文，吴育华，吴振奎,等.单纯形法选择进出基变元的一个新准则[J] .数学的实践与认识，2009，39(14): 75-81.

[8] Arsham H.Initialization of the simplex algorithm:an artificial-free approach[J].SIAM Review，1997，39(8): 736-744.

[9] Arsham H.A computer implementation of the push-and-pull algorithm and its computational comparison with LP simplex method[J].Applied Mathematics and Computation，2005，170(1): 36-63.

[10] Enge A，Huhn P.A counterexample to H Arsham′s “initialization of the simplex algorithm:an artificial-free approach” [J].SIAM Review，1998，40(4): 1-6.

[11] Dongarra J，Golub G，Grosse E，et al.Netlib and NA-Net:building a scientific computing community[J].IEEE Annals of the History of Computing，2008，30(2):30-41.

[12] Bixby R E，Ceria S，McZeal C M，et al.An updated mixed integer programming library: MIPLIB 3.0[J].Optima，1998，54(1): 12-15.

[13] 申卯兴，叶微，刘毅，等.单纯形法中枢轴元素选取准则的改进[J].计算机工程与应用，2003，25(1): 57-58.