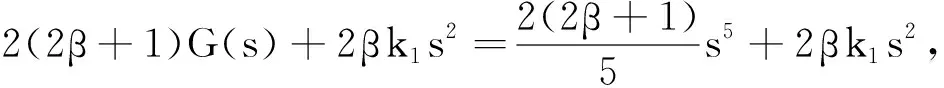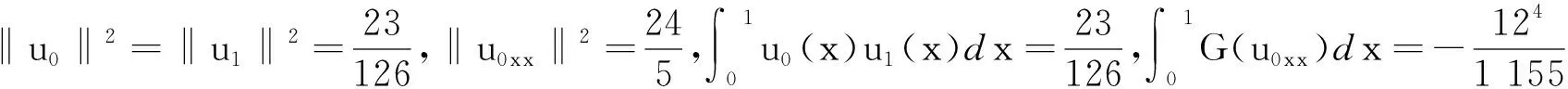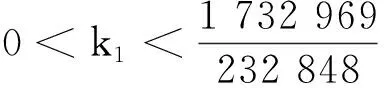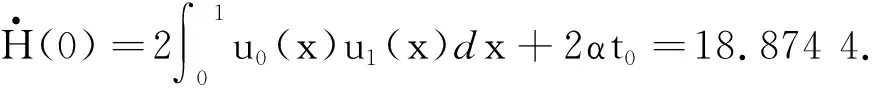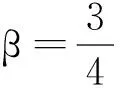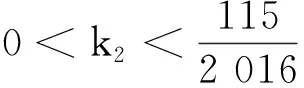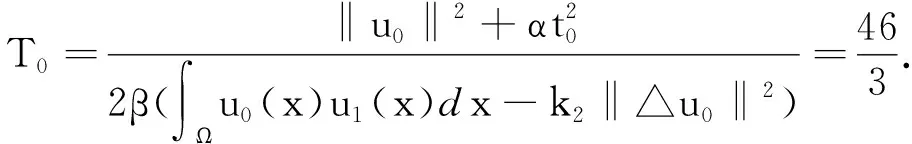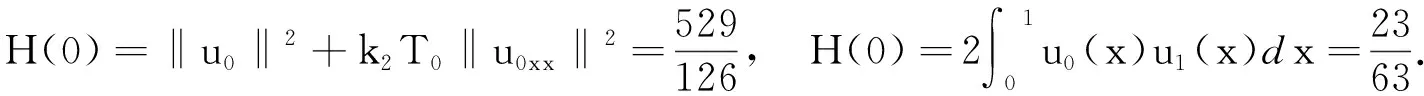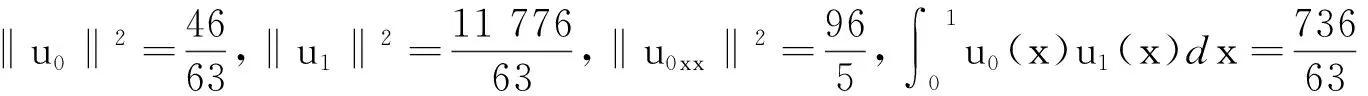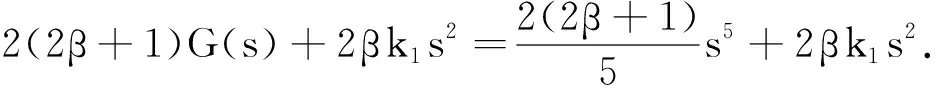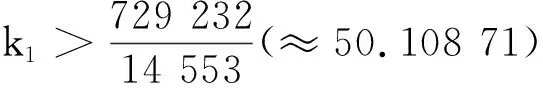一类具阻尼非线性双曲型方程的初边值问题解的爆破

宋瑞丽,霍振宏,苏 婷

(1.中原工学院 信息商务学院,河南 郑州 450007; 2.中原工学院 理学院,河南 郑州 450007;3.河南工程学院 数理科学系, 河南 郑州 451191)

非线性双曲型方程的三维初边值问题

utt+k14u+k24ut+2g(2u)=0,(x,t)∈Ω×(0,T),

(1)

u=0,2u=0,(x,t)∈∂Ω×(0,T),

(2)

(3)

其中,k1,k2>0,u(x,t)为未知函数,RN是给定的非线性函数,Ω是RN中具有光滑边界的有界区域,表示梯度算子,2=△表示Laplace算子,4=△2表示双调和算子,下标t表示对t求偏导数.

方程(1)是在具有阻尼薄膜振动中出现的数学模型[1-2].对于非线性双曲型方程的初边值问题的解在有限时间内失去正规性而发生爆破现象的研究有重要的实际意义，关于问题(1)的其他类型的初边值问题或柯西问题解的性质有许多工作,见文献[3-5],但解决的大都是局部解.本研究用凸性方法证明了初边值问题(1)～(3)不存在整体光滑解，即解必在有限时间内产生爆破现象，并给出了一个例子.

1 整体解不存在定理

为了讨论解的爆破，需要如下引理.

引理设一正的二次可导函数H(t)，对于t≥0，满足不等式

(4)

其中,β>0和A1，A2≥0.

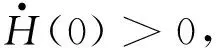
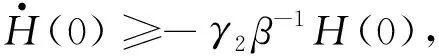
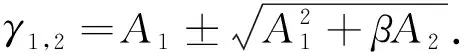
定理假设u0∈H2(Ω)，u1∈L2(Ω)，g(0)=0，G(△u0)∈L1(Ω)并且存在常数β>0使得

sg(s)≤2(2β+1)G(s)+2βk1s2， ∀s∈R，

(5)

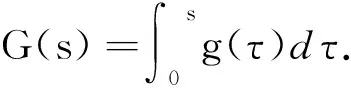
(1)E(0)<0；

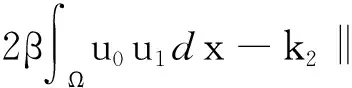
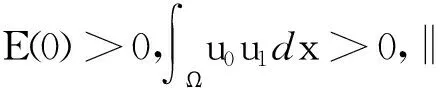
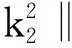
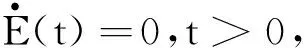
E(t)=E(0)，t>0.

(6)

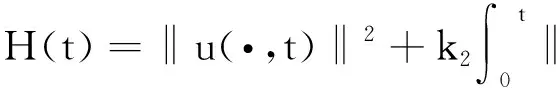
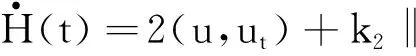
(7)

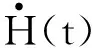
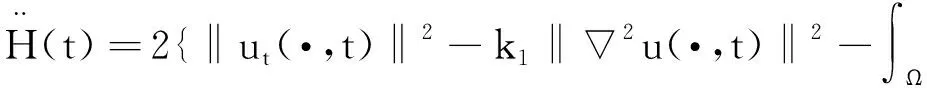
(8)

从(6)、(7)和假定(5)可推出:

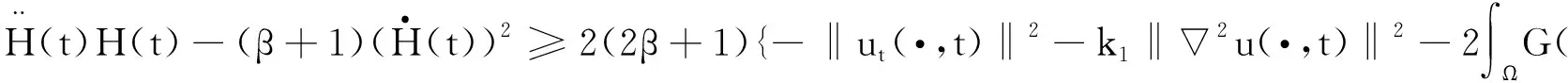
(9)

如果E(0)<0，取α=-E(0)，那么式(9)变为:

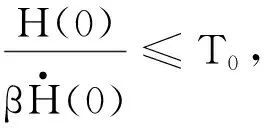
为了完成证明，需要确定T0和t0为正常数.显然，若t0充分大，则

(10)

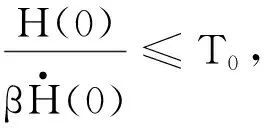
(11)

现在选择t0足够大，使得

(12)

和

(13)

当T0关于t0取最小值时，有

(14)

把式(14)代入式(13)，可得有限常数T0.显然，式(14)中的t0是正数并且满足(10)和(12).

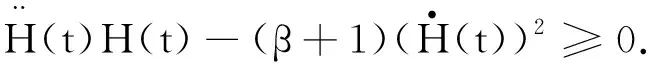
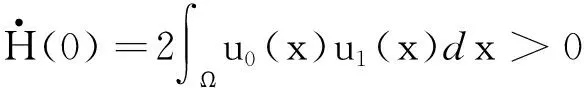
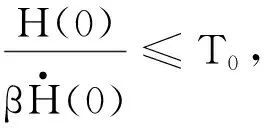
如果E(0)>0，取α=0，那么式(9)变为:

(15)

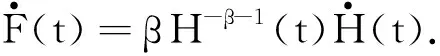
根据式(15)求得:

(16)

(17)

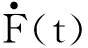
(18)

在式(18)中,对t积分，得 :

(19)

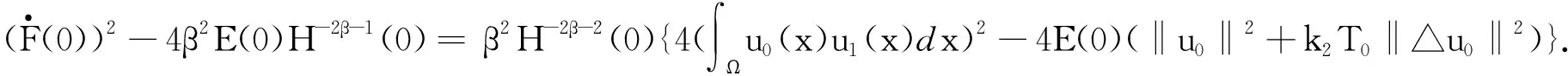
若T0充分小,注意到假定(3)可知:

(20)

(21)

因为4β2E(0)H-2β-1(0)>0，从式(19)可推出

(22)

(23)

由t*的定义知式(23)对所有的t≥0都成立.式(23)对t积分，得

选取T0使得

(24)

由式(24)知

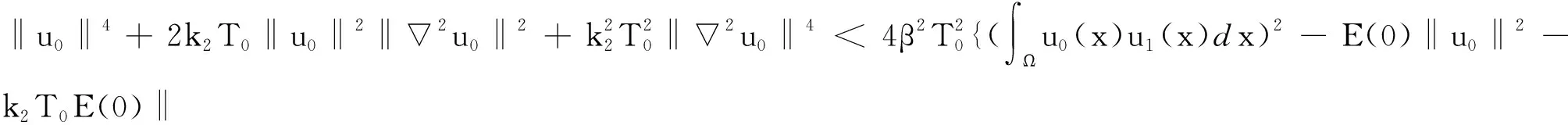
(25)

如果取T0=A0>1，则由式(25)得:

最后，满足 1

2 例子

现举例来说明满足定理条件的函数g(s)，u0(x)和u1(x)是存在的.因为定理对于方程(1)的一维情形仍然成立，为简单起见，只举一维情形的例子.

例考虑下面的初边值问题:

utt+k1uxxxx+k1uxxxxt+g(uxx)xx=0,(x,t)∈(0，1)×(0,T),

(26)

u(0，t)=u(1，t)=0,uxx(0，t)=uxx(1，t)=0,t∈(0,T),

(27)

u(x,0)=u0(x),ut(x,0)=u1(x),x∈[0，1].

(28)

分3种情形讨论.

(1)E(0)<0的情形.

(29)

E(0)=-1<0，α=-E(0)=1.

(2)E(0)=0的情形.

(3)E(0)>0的情形.

取u0(x)=2(x4-2x3),u1(x)=32(x4-2x3)和g(s)=s4，那么

由上面的关系式知u0(x)∈H2(0,1)，u1(x)∈L2(0，1)，G(u0xx)∈L1(0，1)，

所以,当β=2和k1>0时，g(s)满足一维情形下定理中的假设式(5),于是有

(30)

因为

取1

从而满足定理一维情形的条件，于是存在

参考文献：

[1] Banks H T,Gilliam D S,Shubov V I.Global solvability for damped abstract nonlinear hyperbolic system[J].Differential and Interal Equations,1997,10 (2) : 309-332.

[2] Salim A M.Global existence and nonexistence in a system of Petrovsky[J].Journal of Analysis,2002(265):296-308.

[3] Levine H A.Some additional remarks on the nonexistence of global solutions to nonlinear wave equation [J].SIAM J Math Anal,1974,(5):138-146.

[4] Chen G,Wang Y,Zhao Z,Blow-up of solution of an initial boundary value problem for a damped nonlinear hyperbolic equation[J].Applied Mathematics Letters,2004,(17):491-497.

[5] Chen G W.Initial boundary value problem for a damped nonlinear hyperbolic equation[J].Partial Diff Eqs,2003,16(1)：49-61.