一类具有三次项混沌吸引子的Si′lnikov混沌

李建平，王 霞

(河南工程学院 数理科学系，河南 郑州 451191)

混沌系统在很多领域都具有广泛的应用，比如通信、信息处理、计算机图像处理、图像数据加密和信号检测等.目前，非线性混沌系统的奇怪吸引子的研究是一个热门课题，受到了越来越多的专家和学者的关注，比如Chen系统[1]、Lorenz系统[2]、Lü系统[3]与Liu系统[4]等.文献[5]给出了一类具有三次项的混沌吸引子，文献[6]和文献[7]介绍了该系统混沌行为的存在性并给出了该系统的定性特征，但对这类系统产生混沌的机制并没有详细给出，本研究将利用待定系数法和Si′lnikov定理解析地给出此类系统产生混沌的机制.

1 平衡点分析

考虑如下具有三次项的混沌吸引子：

(1)

其中，x，y，z是状态变量，a为实参数.通过简单的计算可知，系统只有一个平衡点O(0，0，0)，系统(1)在平衡点O(0，0，0)处的Jacobi矩阵为：

其相关的特征方程为：

F(λ)=λ3+aλ2+1.

(2)

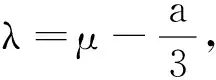
(3)

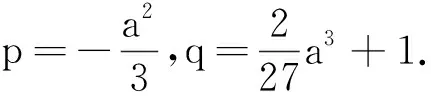
(4)

因此，Δ>0和(4)保证平衡点O(0，0，0)是一个鞍焦点.

2 混沌运动的分析

考虑如下的三维自治系统：

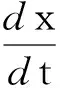
(5)

其中，向量函数f(x)：R3→R3∈Cr(r≥2).Si′lnikov 同宿轨道和Si′lnikov混沌的存在性如定理1.

定理1[8]假设系统(5)的平衡点xe是一鞍焦点，系统的Jacobi矩阵在该平衡点处的特征值为γ和ρ±iω，满足如下的Si′lnikov不等式：

ω≠0，γρ<0， |γ|>|ρ|>0，

并假设存在连结xe到其自身的同宿轨道，则

(1) 存在定义在同宿轨邻域内的可数Smale马蹄；

(2) 对f任意充分小的C1扰动g，扰动系统

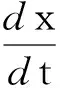
(6)

至少存在有限的定义在同宿轨附近的Smale马蹄；

(3) 原系统(5)和扰动系统(6)均具有Smale马蹄意义下的混沌.

将系统(1)中前两个方程代入第三个方程，得：

(7)

如果x(t)找到的话，y(t)和z(t)也可以被x(t)所决定.因此，寻求系统(1)的同宿轨可转化为寻求满足(7)的函数x(t)=φ(t)且满足当t→±∞时，φ(t)→0，即可用待定系数法找到连接O点的同宿轨道.

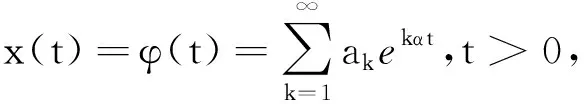
即

(8)

比较上式，取等式两边ekαt(k≥1)的同次幂系数，得到如下结果：

当k=1，有

α3+aα2+1=0 .

(9)

式(9)恰好是系统(1)在平衡点O处Jacobi矩阵的特征方程，故当Δ>0时，(9)式有唯一负实根α<0，且当k>1时，有F(kα)≡k3α3+ak2α2+1≠0.

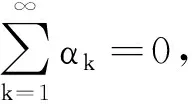
当t<0时，利用变量代换τ=-t(t<0)，系统(1)变为：

(10)

把式(10)中前两个方程带入第三个方程中可得：

(11)

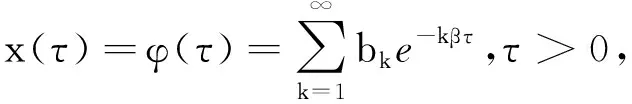
(12)

比较等式两边e-kβτ(k≥1)的同次幂系数，当k=1时，有β3+αβ2+1=0恰好是方程(9)，故α=β.当k>1时，同t>0情形，有b2k=0，b2k+1=Ψ2k+1(β)b12k+1，其中Ψ2k+1(β)同G2k+1(α).当a1=b1时，Ψ2k+1(β)=G2k+1(α)，事实上，方程(12)即是方程(8).

由系统的对称性，可知其同宿轨的第一个分量具有如下的形式：

(13)

由上面的讨论和定理1，得到下面的定理：

定理2如果Δ>0和(4)成立，则系统(1)具有连接平衡点O自身的同宿轨道，其第一个分量具有公式(13)的形式，从而存在Smale马蹄意义下的混沌.

3 结语

本研究讨论了一类三维系统的混沌动力学行为.利用待定系数法和Si′lnikov定理详细研究了一类具有三次项的混沌吸引子的混沌运动，证明了该系统的同宿轨道的存在性和Smale马蹄意义下的混沌的存在性，并给出了同宿轨道的精确表达式，从而给出了系统产生混沌的判据.

参考文献：

[1] Zhou T S,Chen G R,Yang Y.Chen′s attractor exists[J].International Journal of Bifurcation and Chaos,2004(14):3167-3178.

[2] Wang J,Zhao M,Zhang Y,et al.Si′lnikov-type orbits of Lorenz-family systems[J].Physica A,2007(37):438-446.

[3] Lü J,Chen G.A new chaotic attractor coined[J].International Journal of Bifurcation and Chaos,2002(12):659-661.

[4] Zhou X,Wu Y,Li Y,et al.Hopf bifurcation analysis of the Liu system[J].Chaos,Solitons & Fractals,2008(36):1385-1391.

[5] Malasoma J M.What is the simplest dissipative chaotic jerk equation which is parity invariant[J].Phys Lett A,2000(264):383-389.

[6] Sprott J C.Chaos and Time-Series Analysis[M].New York:Oxford University Press,2003.

[7] Vicha T,Dohnal M.Qualitative feature extractions of chaotic systems[J].Chaos,Solitons & Fractals,2008(38):364-373.

[8] Silva C.Si′lnikov theorem-a tutorial[J].IEEE Transactions on Circuits and Systems I,1993,40 (10):678-682.