离散模糊双线性系统的输出反馈控制
孟金涛,孟晓玲,毛北行
(郑州航空工业管理学院 数理系,河南 郑州 450015)
双线性系统是一类特殊的非线性系统,对于很多实际系统,当用线性系统不能描述时,往往可用双线性系统模型来建模[1],基于T-S模型的双线性模型的模糊控制引起了控制界的广泛关注[2-5],而目前对模糊双线性系统的研究用的都是状态反馈控制器,关于静态输出反馈控制器的结果很少.静态输出反馈控制直接利用系统的输出量来设计控制器,不用考虑系统状态是否可测量,且静态输出反馈控制器的结构简单,具有良好的应用价值.本课题研究了一类离散的基于T-S双线性模型的输出反馈控制问题,通过Lyapunov稳定性理论得到了系统稳定的条件,并把最终结果转化为线性矩阵不等式.
1 系统描述
由T-S模型描述的模糊双线性系统,其第i条规则为:若ξ1(k)=F1i,ξ2(k)=F2i,…,ξv(k)=Fvi,其中i=1,2,…,s,则
(1)
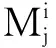
(2)
系统的输出反馈控制律可以表示为:
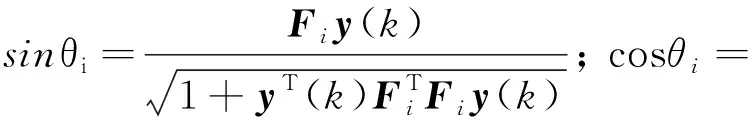
全局控制律可表示为:
(3)
在控制律(3)的作用下,整个闭环系统的方程可表示为:
(4)
其中,Λi=Ai+ρisinθiNi+ρicosθiBiFiCi.
引理1对适当维数的矩阵X,Y则下式成立:XTY+YTX≤ε-1XTX+εYTY.

(1)s<0;
2 主要结果
定理1对给定的常数ρi, 如果存在对称正定的矩阵Pi和矩阵Fi满足下述不等式:
(5)
其中,Λi=Ai+ρisinθiNi+ρicosθiBiFiCi, 则闭环系统(4)渐近稳定.
证明选取Lyapunov函数V(k)=xT(k)Pix(k), 很容易得到定理1.
定理2对给定的常数ρi, 如果存在对称正定的矩阵Pi和矩阵Fi满足下述不等式:
(6)
则闭环系统(4)渐近稳定.
证明引入 Lyapunov 函数V(k)=xT(k)Pix(k).
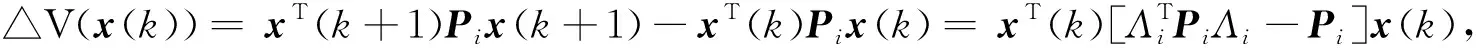
利用引理2,由(6)很容易得到△V(x(k))<0,从而闭环系统渐近稳定.
3 结束语
研究了一类离散的基于T-S双线性模型的输出反馈控制问题,通过 Lyapunov 函数得到系统稳定的条件,并把最终结果转化为线性矩阵不等式.
参考文献:
[1] Li T H S,Tsai S H.T-S fuzzy bilinear model and fuzzy controller design for a class of nonlinear systems [J].IEEE Trans Fuzzy Syst,2007,15(3): 494-505.
[2] 郭岗,牛文生.模糊双线性关联系统的反馈控制[J].北京邮电大学学报,2011,34(1):135-139.
[3] Li T H S,Tsai S H.Robust fuzzy control for a class of uncertain discrete fuzzy bilinear systems [J].IEEE Trans Syst Man Cybe,2008,38(2):510-526.
[4] Tsai S H,Li T H S.Robust fuzzy control for a class of fuzzy bilinear systems with time-delay[J].IEEE Trans Fuzzy Syst,2009,17(1):128-137.
[5] Li T H S,Tsai S H.T-S fuzzy bilinear modle and fuzzy controller design for a class of nonlinear systems [J].IEEE Trans Fuzzy Syst,2007,3(15):494-505.

