基于改进单纯形法的冗余证券的判别
吴卓然
(中央财经大学金融学院,北京 100081)
基于改进单纯形法的冗余证券的判别
吴卓然
(中央财经大学金融学院,北京100081)
对于一般读者来说,从理论上确定冗余证券是比较难懂的,但我们可以用线性相关性或者矩阵的方法加以判别。本文用求解线性规划问题的改进单纯形法,来判别冗余矩阵,无疑为学界提供了一种新的思路。
改进;单纯形法;冗余证券
一、引言
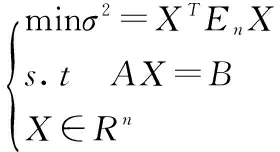
二、冗余证券的一般判别方法
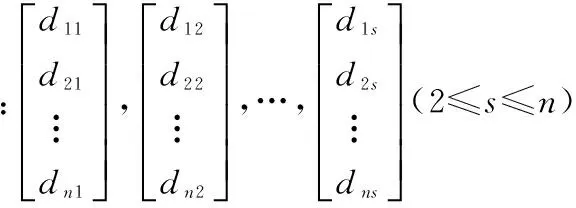
1.线性相关性判别法
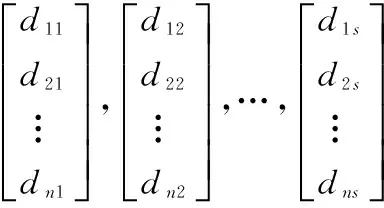
2.矩阵秩判别法

三、改进的单纯形法Simplex algorithm
1.单纯形法
1947年,美国数学家丹齐克(George Bernard Dantzig)提出了一种求解线性规划问题的通用方法——单纯形法。其理论根据是:当线性规划问题的可行域是维向量空间中的多面凸集时,如果存在最优值,则必在该凸集的某顶点处达到。这时,我们称顶点所对应的可行解称为基本可行解。其基本思路:先找出一个基本可行解,对它进行判别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再判别;若仍不是,则再转换,按此重复进行。由于基本可行解的个数有限,故经有限次转换必能得出问题的最优解。当然,问题无最优解也可用此法判别。
2.改进的单纯形法
当用单纯形法求解现行规划问题时,每行每列的数据都要计算,而大部分行列的数据在下一步计算时并不需要;也即是说用单纯形法求解线性规划也不简便。1953年,丹齐克提出改进单纯形法,以改进单纯形法每次迭代中积累起来的进位误差。其基本步骤和单纯形法大致相同,主要区别是在逐次迭代中不再以高斯消去法为基础,而是先通过旧基阵的逆去去直接计算新基阵的逆,再确定检验数。这样做基减少迭代中的累积误差,并且提高计算精度,改进的单纯形法就是用矩阵的方法描述单纯形法,只不过在求逆矩阵是用了一种新的方法。其原理如下:
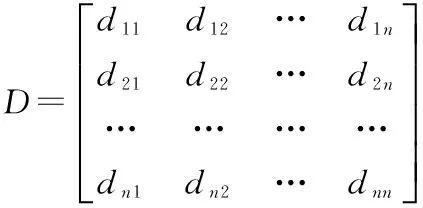
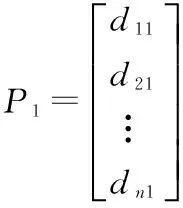
显然D-1=En…E2E1。
3.改进单纯形法的冗余证券的判别
改进的单纯形法虽说是求矩阵D逆矩阵的一种方法,但是当证券的支付矩阵D不是方阵时,我们也可以用它来判断某一个证券是不是冗余证券。

4.矩阵秩判别法
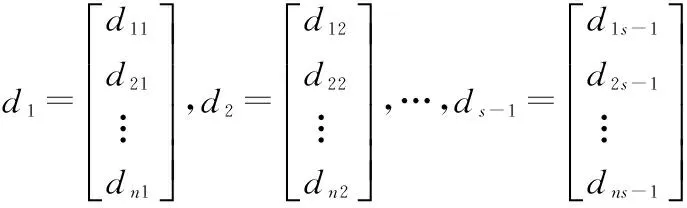
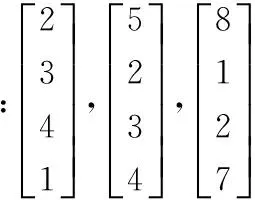
四、结论
是否是冗余证券,可以用向量的线性相关性来判断,也可以用矩阵的秩来判断;当然,改进单纯形法不失是一种好方法,其简单、明了、易懂。
[1] 郭宇权.金融衍生产品的数学模型[M].北京:科学出版社,2012.
[2] 宋逢明.金融工程原理——无套利均衡分析[M]. 北京:清华大学出版社,2003.
[3] 陈蓉,方昆明.波动率风险益酬:时变特征及影响因素[J].系统工程理论与实践,2011,31(4).
[4] 蒋福坤,刘正春.非正定方差阵下的证券组合投资模型研究[J].数学的实践与认识,2008,38(3).
[5] 龙朝阳,屠新曙.证券组合投资中的冗余证券问题[J].中国管理科学增刊,2001,9.
[6] 周海林,吴鑫育,丁忠明,汪寿阳.权证是冗余证券吗?基于沪深交易所的经验证据[J].系统工程与实践,2013,33(7).
[7] 张莉.Markowitz投资组合风险偏好模型研究[J].新疆大学学报(自然科学版),2015,22(5).
[8] 张莉.风险偏好模型研究[D].新疆大学硕士论文,2005.
2014年北京市大学生创新创业训练计划项目(BEIJ2014110044)

