区间数级数的理论研究

高德宝

（黑龙江八一农垦大学理学院，大庆 163319）

区间数级数的理论研究

高德宝

（黑龙江八一农垦大学理学院，大庆 163319）

文章在已知实数项级数收敛及区间数列收敛概念的基础上，具体阐述了区间数项级数的定义及其性质.然后，给出了几个关于正区间数项级数敛散性判断定理与推论.最后，关于一般项区间数级数敛散性的判别作了讨论.

区间数；级数；收敛；发散

1 引 言

区间分析或称区间数学是最近四十年来发展起来的一个新的数学分支.目前，区间分析的主要研究对象是区间数的应用，而关于区间数以及区间数集的研究却很少.文献［1，2］给出了区间数的定义及其基本运算，介绍了区间数在计算方法、自动控制中的具体应用.虽然，区间分析学的有关理论已被越来越多地应用到各个领域，如文［3，4］，但它的基础性理论还有很大的研究空间.本文基于文献［1，2，5，6，7］，结合数学分析的相关理论，给出区间数级数收敛的定义以及多个判别方法.

2 区间数的概念及其基本运算

定义1 称A＝［al，ar］为一个区间数.当al＝ar时，区间数就退化为一实数.

定义2 给定两个区间数A＝［al，ar］，B＝［bl，br］，两个区间数之间有如下的运算

上面所提及的理论基本上来源于文献［3］.相应于正数、负数与实数的模的定义，我们给出区间数对应的定义.

定义3 给定一个区间数［x，y］.若x＞0，称其为正区间数.若y＜0，称其为负区间数.

定义4 给定一个区间数［x，y］.对于所有的t∈［x，y］，称由所构成的闭区间为区间数［x，y］的模，记作｜［x，y］｜.

由上面的定义，可得计算公式

定义5 设｛［an，bn］｝为一区间数列，若存在一实数M＞0，使得

则称其为有界区间数列.

定义6 设｛［an，bn］｝为区间数列，若an≤an＋1，bn≤bn＋1，则称其为单调递增区间数列；若an≥an＋1，bn≥bn＋1，则称其为单调递减区间数列.

定义7 设｛［an，bn］｝为区间数列，［a，b］为区间常数.若对任给的正数ε，总存在正整数N，使得当n＞N时，有｜an-a｜＋｜bn-b｜＜ε.则称区间数列｛［an，bn］｝收敛于［a，b］，常数［a，b］称为区间数列｛［an，bn］｝的极限，并记作［an，bn］＝［a，b］.若区间数列｛［an，bn］｝没有极限，则称其不收敛，或称其为发散数列.

3 区间数级数的收敛性

定义8 给定一个区间数列｛［an，bn］｝，对它的各项依次用“＋”号连接起来的表达式

称为区间数项无穷级数或区间数项级数（可简称为区间数级数），其中［an，bn］称为区间数项级数的（1）通项或一般项.区间数项级数（1）也可简单写作∑［an，bn］.

区间数级数（1）的前n项之和，记为

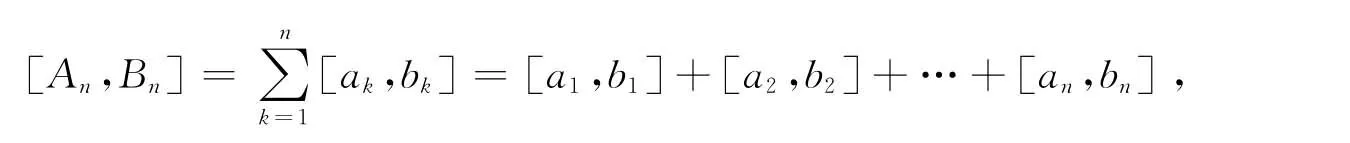
称它为区间数项级数（1）的第n个部分和，简称部分和.

定义9 若区间数项级数（1）的部分和数列｛［An，Bn］｝收敛于［A，B］，则称区间数项级数（1）收敛，称［A，B］为区间数项级数（1）的和，记作

若｛［An，Bn］｝是发散区间数列，则称区间数项级数（1）发散.

根据区间数列极限的定义，有下面的定理.

定理2 区间数项级数∑［an，bn］收敛的充要条件是：实数项级数∑an，∑bn（an≤bn）收敛.

推论区间数项级数∑［an，bn］发散的充要条件是：实数项级数∑an或∑bn（an≤bn）发散.

定理3 区间级数（1）收敛的充要条件是：任给正数ε＞0，总存在正整数N，使得当m＞N以及对任意的正整数p，都有

推论若级数（1）收敛，则

定理4（线性运算） 若区间数级数∑［an，bn］与∑［cn，dn］都收敛，则对任意的实常数k，l，级数∑k［an，bn］＋l［cn，dn］亦收敛，且

定理5 去掉、增加或改变级数的有限项并不改变级数的敛散性.

定理6 在收敛级数的项中任意加括号，既不改变级数的收敛性，也不改变它的和.

4 正区间数项级数

若区间数项级数各项均是正区间数或均是负区间数，则称它为同号级数.对于同号级数，只需研究各项都是由正区间数组成的级数——称为正区间项级数.如果级数的各项都是负数，则它乘以-1后就得到一个正区间项级数，它们具有相同的敛散性.

定理7 正区间数项级数∑［an，bn］收敛的充要条件是：实数项数列｛Bn｝有界，即存在某正数M，对一切正整数n有Bn≤M.

对于正区间项级（1）而言，因为an≤bn，若∑bn收敛，则∑an必收敛；若∑an发散，则∑bn必发散.故对于其收敛性而言，我们只需讨论∑bn收敛性.而正数项级∑bn收敛性的充要条件是它的部分和数列有界.故定理7易证.定理7与下面的两个定理是等价的.

定理8 正区间数项级数∑［an，bn］收敛的充要条件是正项级数∑bn收敛.

推论正区间数项级数∑［an，bn］发散的充要条件是实数项级数∑an发散.

定理9 设∑［an，bn］是正区间项级数，∑cn是正项级数.如果存在某正整数N，对一切n＞N都有

（i）bn≤cn且∑cn收敛，则正区间数项级数∑［an，bn］收敛.

（ii）cn≤an且∑cn发散，则正区间数级数∑［an，bn］发散.

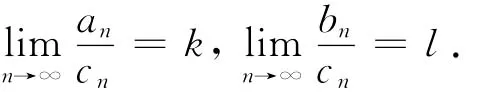
（i）当0＜l＜＋∞时，级数∑［an，bn］和级数∑cn同时收敛或同时发散.

（ii）当k＝0且级数∑cn发散时，级数∑［an，bn］发散.

（iii）当k＝＋∞或l＝＋∞且级数∑cn发散，则级数∑［an，bn］也发散.

证根据数学分析［5］中的比较原则，当0＜l＜＋∞时，级数∑bn和级数∑cn同时收敛或同时发散，故根据定理8可得：结论（i）是成立的.当k＝0且级数∑cn发散时，级数∑an是发散的，根据定理8的推论可知：结论（ii）是成立的.当k＝＋∞或l＝＋∞且级数∑cn发散时，级数∑an或∑bn发散，故结论（iii）是成立的.

（i）当q＜1时，正区间项级数∑［an，bn］收敛.

（ii）当q＞1或p＞1时，正区间项级数∑［an，bn］发散.

定理11（根式判别法） 设∑［an，bn］是正区间项级数，且存在某正整数N及常数l，

（i）若对一切n＞N，成立不等式nbn≤l＜1，则正区间项级数∑［an，bn］收敛；

（ii）若对一切n＞N，成立不等式nbn≥1，则正区间项级数∑［an，bn］发散.

（i）当l＜1时，正区间项级数∑［an，bn］收敛；

（ii）当k＞1或l＞1时，正区间项级数∑［an，bn］发散.

4 一般项区间数级数

定义10 若区间数项级数的正、负区间数相间，即

则称其为为交错区间数级数.

定理12（莱布尼兹判别法） 若交错区间数级数（2）满足下述两个条件：

根据数学分析［5］中的莱布尼兹定理，数项级数∑（-1）n-1an，∑（-1）n-1bn是收敛的.故交错区间数项级数（2）是收敛的.

推论若区间数级数（2）满足莱布尼兹判别法的条件，则收敛的区间数级数（2）的余项估计式为

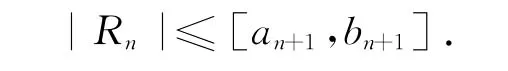
定义11 若区间数项级数［a1，b1］＋［a2，b2］＋…＋［an，bn］＋…的各项绝对值所组成的级数

收敛，则称原区间项级数为绝对收敛级数.

定理13 绝对收敛的区间数项级数一定收敛.

故级数∑an，∑bn是收敛的，从而级数∑［an，bn］是收敛的.

由区间数的乘法运算，我们会得到如下两个区间数列乘积的级数：

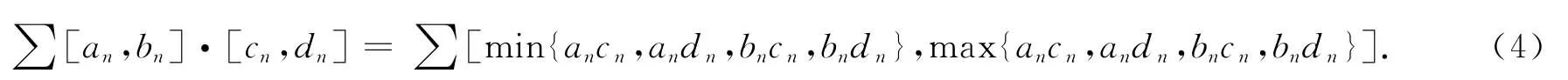
定理14（阿贝尔判别法） 若｛［an，bn］｝为单调递增（或递减）的有界区间数列，且区间数项级数∑［cn，dn］收敛，则区间数项级数（4）收敛.

证因为｛［an，bn］｝为单调递增（或递减）的有界区间数列，所以数列｛an｝，｛bn｝是单调递增（递减）且有界的.因为区间数项级数∑［cn，dn］收敛，所以数项级数∑cn，∑dn是收敛的.

根据数学分析［5］中的阿贝尔判别法可知，四个数项级数

是收敛的.即区间数项级数（4）是收敛的.

此定理的证明过程需用数学分析［5］中的狄利克雷判别法定理，它的证明过程与定理14的基本相同.故其证明过程略.

［1］ Moore R E.Interval analysis［M］.Englewood：Prentice-Hall，1966.

［2］ Moore R E，Kearfott R B，Cloud M J.Introduction to Interval Analysis［M］.SIAM：2008.

［3］ Chen P Y.An interval estimation for the number of signals［J］.Signal Processing，2005，85（3）：1622-1633.

［4］ Hansen E.Global Optimization Using Interval Analysis the Multi-Dimensional Case［J］.Numerische Mathematik，1980，34（3）：247-270.

［5］ Chen C Z.Mathematical Analysis［M］.Higher Education Press：2005.

［6］ Seqngupta A，Pal K.On comparing interval numbers［J］.European Journal of Operation Research，2000，127（1）：28-43.

［7］ Chanas S，Zielinski P.Ranking fuzzy interval numbers in the Setting of random sets-further results［J］.Information Scienee，1999，117（8）：201-207.

Study on The Theory of Interval Series

GAO De-bao
（College of Sciences，Heilongjiang Bayi Agricultural University，Daqing 163319，China）

The definition and its properties of interval number series is described in detail，which is based on the concepts of real series and interval sequences.Then，it gives a few theorems and deductions of the convergence and divegence of positive interval number series.At last，the he convergence and divergence of the common interval numbers series is discussed.

interval number；series；convergence；divergence

O173.1

A

1672-1454（2012）03-0042-05

2009-11-07