一类时滞三维离散神经网络模型的稳定性和分支

杨 慧

（安徽大学数学科学学院，合肥 230039）

一类时滞三维离散神经网络模型的稳定性和分支

杨 慧

（安徽大学数学科学学院，合肥 230039）

讨论了一类带时滞的离散三维神经网络模型.利用数学分析技巧，对线性化系统的特征根进行分析，获得了平衡点的局部稳定性及分支点，并利用规范型和中心流形理论得出了决定分支方向和稳定性的公式.

离散系统；神经网络；稳定性；分支

1 引 言

在文［1］中作者建立了如下的模型：

本文考虑更一般的系统

其中xi是第i个神经元的活动状态，正常数τ和b分别表示两个神经元之间的时滞和连接权值，fij→是C1类信号传输函数且fij（0）＝0，f′ij（0）＝1，i，j＝1，2，3.

在系统（2）中，令xi（τt）＝ui（t），i＝1，2，3，得

将系统（3）离散化，得

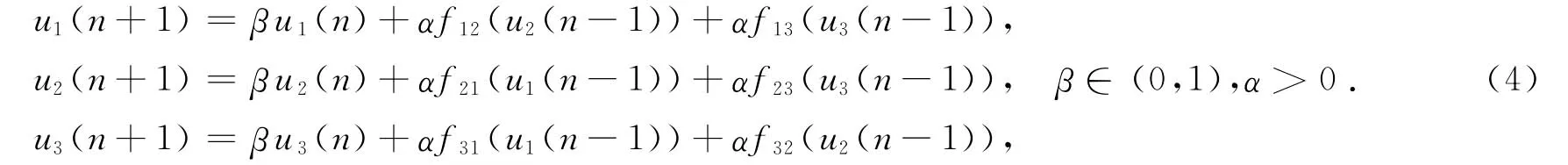
2 分支的存在性

显然（0，0，0）点是系统（4）的平衡点，在此平衡点线性化系统（4），得

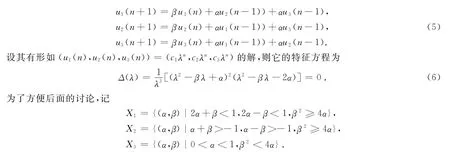
记φj（j＝0，1，2）为v（t）的3个零点，则可得φ0＝0，φ1＝arccos，φ2＝π，且u（φ0）＝1-β，u（φ2）＝1＋β.由文［2］的结论可得

定理3 （i）当且仅当（α，β）∈｛（α，β）｜X2∪X3且2α＝1-β，-α≠u（φ1）｝时，系统（4）在平凡解处存在Pitchfork分支；

（ii）当且仅当（α，β）∈｛（α，β）｜X2∪X3且2α＝1＋β，-α≠u（φ1）｝，系统（4）在平凡解处存在Flip分支；

（iii）当-α＝u（φ1），2α≠u（φ0），u（φ2）时，系统（4）在平凡解处存在Neimark-Sacher分支.

定理1 当（α，β）∈X1∩（X2∪X3）时，系统（4）的平凡解是局部渐进稳定的.

证可验证当（α，β）∈X1∩（X2∪X3）时，｜λ｜＜1.

定理2 下列（i）-（iii）中的任一情形成立，系统（4）的平凡解是不稳定的.

则μ＝-α，2α时，P（λ）中对应的λ值为特征方程（6）的解.定义Σ曲线如下：

3 分支的方向和稳定性

本节主要采用文［5］中介绍的规范型理论和中心流形理论方法，来研究系统（4）分支的方向和稳定性.进一步作如下假设：

（H1）fij＝f∈C3），f（0）＝0，f‴（0）≠0，i，j＝1，2，3.

首先考虑Neimark-Sacher分支，作如下的假设：

（H2）β2＜4α，-α＝u（φ1），2α≠u（φ0），u（φ2），记此时β＝β＊.

采用同文［2］中相同的记号u0＝u（φ1），λ0＝.设U是U（n）的第j个分量，F：6→6，

其中Fj（Un）是F（Un）的第j个分量，则系统（4）可重新改写成

设A＝D F（0），B＝D2F（0），C＝D3F（0），易知det（λI d-A）＝λ3Δ（λ）.

由以上讨论，有以下的结论.

定理4 在条件（H1）和（H2）下，系统（4）在β＝β＊处存在Neimark-Sacher分支，分支的方向和稳定性由sgn｛f‴（0）｝来决定.进一步有：若f‴（0）＞0（或＜0），则Neimark-Sacher分支是上临界（或下临界）的，也即当-α＞u（φ1）（或＜u（φ1））时，系统（4）出现闭的渐进稳定（或不稳定）的不变曲线分支.

证当-α＝u（φ1）时，有α＝1，则

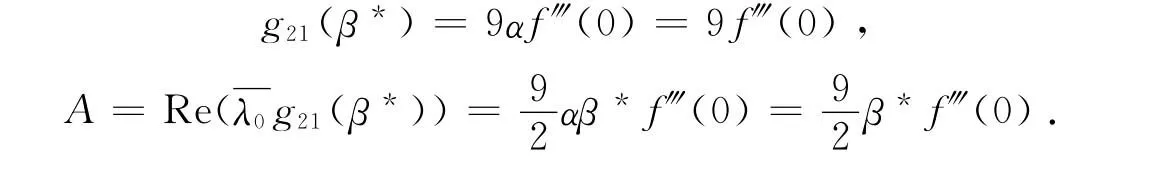
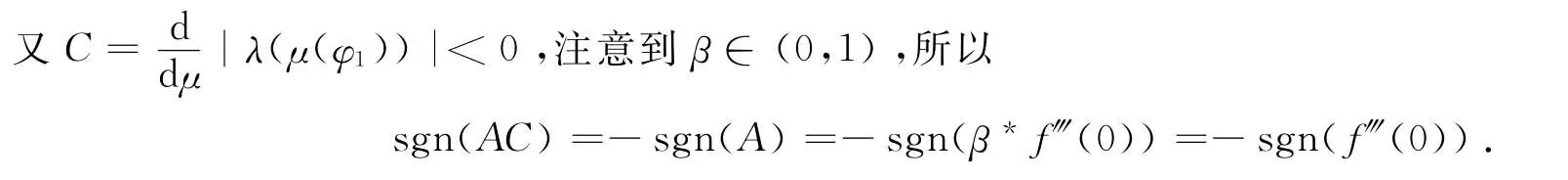
接下来考虑Pitchfork分支的方向和稳定性，为此做如下假设：

（H3）（α，β）∈｛（α，β）｜X2∪X3且2α＝1-β，-α≠u（φ1），记此时β＝β＋＝1-2α.由定理3（i）知，当β＝β＋时，Δ（λ）有一根λ＝1，则此时A在单位圆周上也有一根λ＝1在上一段的讨论中.用1代替λ0，可得相应的p，q的表达式.

对任意向量U∈R R6能唯一地表示成U＝z q（β）（对某个z∈R R），显然z＝〈p（β），U〉，则系统（9）被重新改写成

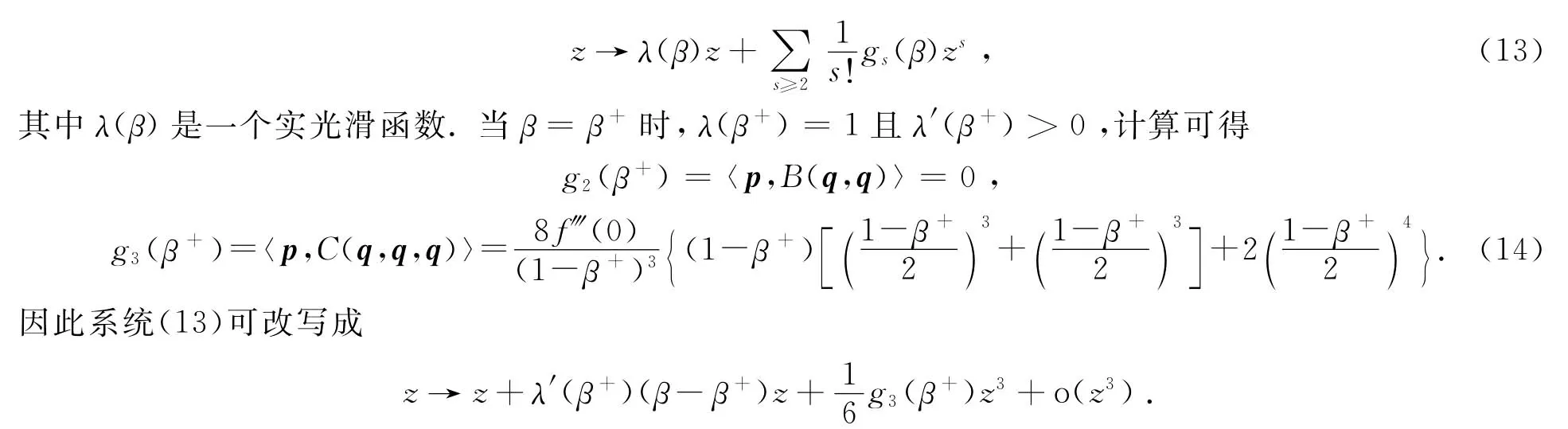
定理5 在条件（H1）和（H3）下，系统（4）在β＝β＋附近存在Pitchfork分支，分支的方向和稳定性由sgn｛f‴（0）｝来决定.进一步有：若f‴（0）＜0（或f‴（0）＞0），系统（4）在2α＞1-β（或2α＜1-β）时有两非平凡解存在；当2α穿过1-β时，这两非平凡解在原点重合；当2α＜1-β（或2α＞1-β）时，系统（4）只剩下平凡解一个解，而且当-α＞u（φ1）时，这两非平凡解是稳定（或不稳定）的.

证由于β∈（0，1），所以（14）式右边的符号由f‴（0）来决定，而

最后，利用类似上面的讨论方法可得Flip分支的方向和稳定性，作假设如下：

（H4）（α，β）∈｛（α，β）｜X2∪X3且2α＝1＋β，-α≠u（φ1）｝，记此时β＝β-＝2α-1，则系统（4）在β＝β-处的三阶规范型是

其中λ′（β-）＜0，g3（β-）＝6αf‴（0）.

定理6 在条件（H1）和（H4）下，系统（4）在β＝β-附近存在Flip分支，分支的方向和稳定性由sgn｛f‴（0）｝来决定.进一步有：若f‴（0）＜0（或f‴（0）＞0），系统（4）的Flip分支是上临界（或下临界）的，也即当2α＞1＋β（或2α＜1＋β）时系统（4）存在2—周期解，且当-α＞u（φ1）时该解是稳定（或不稳定）的.

［1］ Lin Y，Lemmert R，Volkmann P.Bifurcation of periodic solution in a three-unit neural network with delay［J］.Acta.Math.Appl.Sin.，2001，17（2）：375-382.

［2］ Guo S，Huang L.Stability and bifurcation in a discrete system of two neurons with delays Nonlinear Anal［J］.Real World Appl.，2008，9（4）：1323-1335.

［3］ Yuan Z，Hu D，Huang L.Stability and bifurcation analysis on a discrete-time neural network［J］.Comput.Math.Appl.，2005，177：89-100.

［4］ Sharyer L，Campbell S A.Stability bifurcation and multistability in a system of two coupled neurons with multiple time delays［J］.SIAM J.Appl.Math.，2000，61：673-700.

［5］ Kuznetsov Y A.Elements of applied bifurcation theory［M］.2ed.，New York：Springer，1998：193-239.

［6］ 杨慧，莫道宏，王良龙.一个离散神经网络模型的分支［J］.合肥学院学报，2009，19（4）：16-19.

Stability and Bifurcation Analysis on a Three-unit Discrete-time Neural Network

YANG Hui
（School of Mathematical Sciences，Anhui University，Hefei 230039，China）

We consider a discrete neural network model.By using the skill of mathematical analysis，we analysis the characteristic roots of corresponding linearization system and obtain local stability of the equilibrium point and bifurcation point.The calculating formula of direction and stability of the bifurcation are obtained by using the normal form theory and the center manifold theorem.

discrete system；neural network；stability；bifurcation

O175.12

A

1672-1454（2012）03-0037-05

2009-10-27；

2010-05-19

国家自然科学基金（10771001）；安徽省自然科学基金（070416225）；安徽省高校人才基金（05025104）；安徽省教育厅自然科学基金重点项目（KJ2009A49）；安徽省高校自然科学基金重点项目和安徽大学研究生部科技创新与重点课程建设项目资助