参数边界条件下奇型Sturm-Liouville算子的半逆问题
王於平, 肖建强
(1.南京林业大学应用数学系,南京 210037; 2.南京工程学院土木工程系,南京 211100)
参数边界条件下奇型Sturm-Liouville算子的半逆问题
王於平1, 肖建强2
(1.南京林业大学应用数学系,南京 210037; 2.南京工程学院土木工程系,南京 211100)
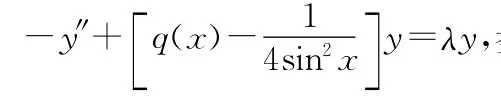
谱;势函数;半逆问题;参数边界条件
1 引言及预备知识
在谱理论中,反谱问题是热点问题之一,1929年Ambartsumyan[1]首次研究了这类问题,1946年以后,Borg[2],Levinson[3],Levitan[4]等都做了大量的工作;近几年,Sakhnovich[6],Rostyslav,Mykytyuk,Yaroslav[7],Koyunbakan,Panakhov[8-9]等研究了半逆问题并取得了一些可喜的成果;Fulton[11],Binding,Browne,Seddighi[12],Binding,Browne,Browne,Waston[13],Zhang,Huang[14]等研究了参数边界条件下Sturm-Liouville的问题,取得了一些有一定影响的成果.由于参数边界条件下Sturm-Liouville的问题比较复杂,这类问题的半逆问题难以解决,文[13]利用Crum和Darboux变换解决了一类Sturm-Liouville问题的特征根的重数、估计式等问题,使研究这类参数边界条件下的奇型Sturm-Liouville算子的半逆问题变为可能,本文利用Koyunbakan和Panakhov的方法和[13]的结果,讨论(0,π)上的势函数中含1/sin2x的Sturm-Liouville算子L满足参数边界条件y(0,λ)=0或y′(0,λ)-hy(0,λ)=0和y′(π,λ)+(aλ+b)y(π,λ)=0的半逆问题,得到了新的结果,即由一组谱和(π/2,π)上的势函数q(x)唯一确定(0,π)上势函数的q(x).本文推广了文[9]的结果.
我们先介绍势函数中含1/sin2x的Sturm-Liouville算子[5].Legendre函数是典型的超几何函数,它是在球对称问题中产生的,这类算子是由经典的Legendre方程经过下面变换得到的.Legendre方程是



根据[13]的结果,满足(8),(9(i)),(10)和(8),(9(ii)),(10)的Sturm-Liouville问题的特征值有三种情况,经过Crum和Darboux变换,其它两种情况都可以转化为满足(8),(9(i)),(10)和(8),(9(ii)),(10)的Sturm-Liouville问题仅具有实的、简单的点谱.因此,我们只要考虑满足(8),(9(i)),(10)和(8),(9(ii)),(10)的Sturm-Liouville问题具有实的、简单的点谱{λn}.根据[5,13,14],不难得到
引理3 (i)当(10)中a≠0时,设满足(8),(9(i)),(10)的Sturm-Liouville问题具有实的、简单的点谱{λn}(n≥0),则{λn}是(10)的根,并满足下面渐近式

(ii)当(10)中a≠0时,设满足(8),(9(ii)),(10)的Sturm-Liouville问题具有实的、简单的点谱{λn}(n≥0),则{λn}是(10)的根,并满足下面渐近式

根据[5],可以得到
引理4[5]当(10)中a=0时,满足(8),(9(ii)),(10)的Sturm-Liouville问题具有实的、简单的点谱{λn}(n≥0),则{λn}是(10)的根,并满足下面渐近式

根据[15],利用变换算子性质,可以得到
引理5 方程(8),(9(ii))的解可写为
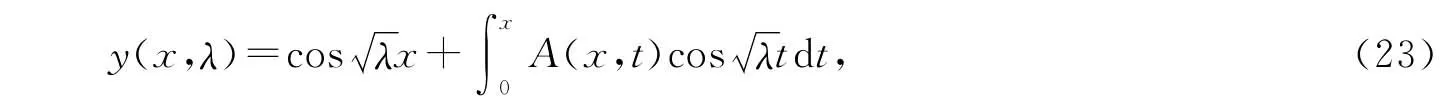
其中积分核A(x,t)是下面的偏微分方程的解
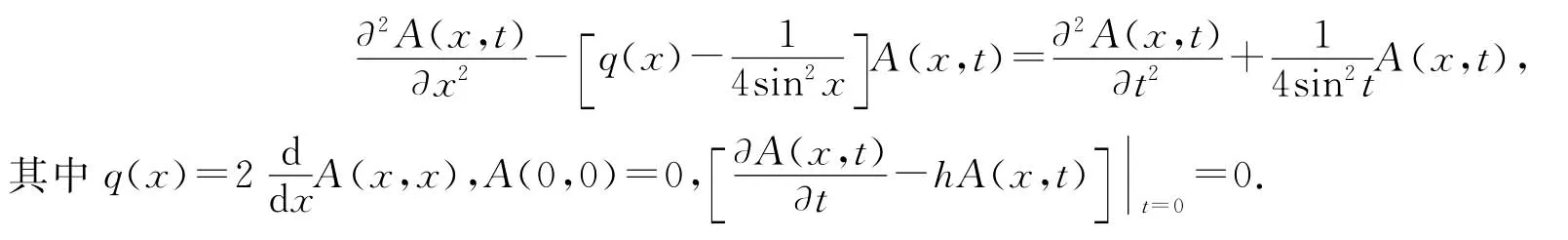
2 主要结果

下面证明本文的定理1及定理2.
定理1的证明 根据引理1,方程(8),(9(i))和(11),(12(i))的解分别为


类似地可以证明定理2,不再赘述.
[1] Ambartsumyan V A.Über eine frage der eigenwerttheorie[J].Zeitschrift für Physik,1929,53:690-695.
[2] Borg G.Eine umkehrung der Sturm-Liouvillesehen eigenwertaufgabe[J].Acta Mathematica,1945,78:1-96.
[3] Levinson N.The inverse Sturm-Liouville problem[J].Mathematica Tidsskrift 13,1949,25-30.
[4] Levitan B M.On the determination of the Sturm-Liouville operator from one and two spectra[J].Mathematics of the USSR Izvestija,1978,12:179-193.
[5] Hochstadt H.The Functions of Mathematical Physics[M].New York:Wiley Interscience,1971.
[6] Sakhnovich L.Half inverse problems on the finite inteval[J].Inverse Problems,2001,17:527-532.
[7] Rostyslav H,Mykytyuk O,Yaroslav V.Half-inverse spectral problems for Sturm-Liouville operators with singular potentials[J].Inverse Problem,2004,20(5):1423-1444.
[8] Koyunbakan H,Panakhov E S.Half-inverse problem for diffusion operators on the finite interval[J].J.Math.Anal.Appl.,2007,326:1024-1030.
[9] Koyunbakan H,Panakhov E S.Half-inverse problem for operators with singular potential[J].Integral Transforms and Special Functions,2007,18(10):765-770.
[10] Hochstadt H,Lieberman B.An inverse Sturm-Liouville problem with mixed given data[J].SIAM Journal of Applied Mathematics,1978,34:676-680.
[11] Fulton C T.Two-point boundary value problems with eigenvalue parameter contained in the boundary conditions[J].Proc.Edinb.Math.Soc.1977,77A:293-308.
[12] Binding P A,Browne P J,Seddighi K.Sturm-Liouville problems with eigenparmeter dependent boundary condtions[J].Proc.Edinb.Math.Soc.1993,37:57-72.
[13] Binding P A,Browne P J,Bowne W J,Watson B A.Transformation of Sturm-Liouville problems with decreasing affine boundary conditions[J].Proc.Edinb.Math.Soc,2004,47:533-552.
[14] Zhang Mao zhu,Huang Zhen you.aclass of sturm-liouville problems with eigenparameter dependent two boundary conditions[J].Acta Analysis Functionalis Applicata,2008,10(4):366-372.
[15] Levitan B M and Sargsjan I S.Sturm-Liouville and Dirac operators[M].Dordrecht:Kluwer Academic Publishers,1990.
Half-inverse Problem for Singular Sturm-Liouville Operators with an Eigenparameter Boundary Condtion
WANG Yu-ping1, XIAO Jian-qiang2
(1.Department of Applied Mathematics,Nanjing Forestry University,Nanjing,Jiangsu 210037,China;2.Department of Civil Engineering,Nanjing Institute of Technology,Nanjing,Jiangsu 211100,China)
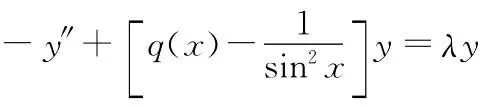
spectrum;potential function;half-inverse problem;eigenparamenter boundary condtions
O175.12
A
1672-1454(2012)03-0053-06
2009-12-04

