树指标马氏链的若干性质
陈晓雪, 李增涛
(江苏大学理学院,镇江 212013)
树指标马氏链的若干性质
陈晓雪, 李增涛
(江苏大学理学院,镇江 212013)
主要研究了树指标马氏链的若干性质,它与一般直线上的马氏链有类似的性质.[关键词]树指标马氏链;单调类定理;条件概率
1 引 言
设T是一局部有限无穷树,选择一个顶点作为根顶点,记为ο顶点.设τ,σ是树图T上任意两个顶点,如果τ处在ο到σ的唯一路径上,则记为τ≤σ,并记为这个路径的边数.对于树图上任意两个顶点σ,τ,记σ∧τ是满足σ∧τ≤σ,σ∧τ≤τ离ο最远的顶点.设σ≠ο记是满足≤σ且=|σ|-1的顶点,即σ是的子代.
定义1[1,2]设T为一树图,G={0,1,2,…}为一可列集合,{Xσ,σ∈T}是定义在概率空间(Ω,F,μP)上在G中取值的随机变量族.设p={p(x),x∈G}是G上一概率分布,P=(μP(y|x))是定义在G2上的随机矩阵.如果∀σ∈T,τi∈T且满足τi∧σ≤,1≤i≤n,∀x,y,x1,…,xn∈G,有
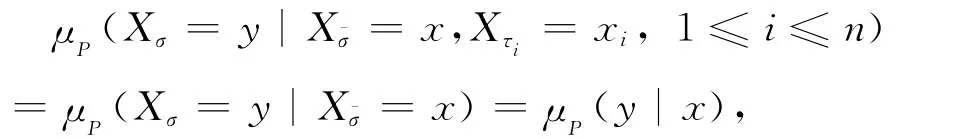
并且μP(Xο=x)=p(x),则称{Xσ,σ∈T}为具有初始分布p与转移矩阵P在G上取值的树指标马氏链.
容易验证以上定义的树指标马氏链定义了一树图T上的Markov随机场.文[3],[4]P.456分别定义了两类特殊的有限状态树指标马氏链.由以上树指标马氏链的定义可知,如果每一个顶点的子代只有一个顶点,则树指标马氏链就是一般的直线上的马氏链.一般直线上的马氏链的性质大家都很熟悉,而树指标马氏链的类似性质并没有相关文献给出,本文由树指标马氏链的定义并且利用单调类定理证明了树指标马氏链的一些性质.
2 主要结果
定理1 设T为一树图,G={0,1,2,…}为一可列集合,{Xσ,σ∈T}为取值在G上由定义1定义的树指标马氏链,则∀A∈σ(Xτ,σ∧τ≤¯σ,τ∈T),有
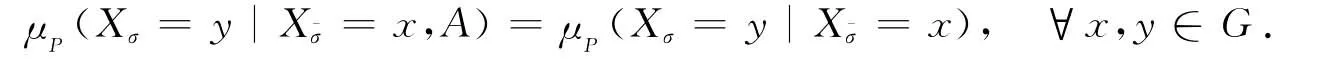
证设xi∈G,τi∈T且τi∧σ≤¯σ,1≤i≤n,由以上树指标马氏链的定义,有

应用单调类定理证明[5]:令

证因为树图是一连通图,所以对∀t∈T且满足σ≤t,总能找到相邻的有限个顶点ti∈T(i=1,2,…,n)且σ≤ti≤t,即ti是在σ到t的唯一路径上.这里我们证明时不妨假设σ到t间只有一个顶点t1,其它情形类似可证.设x1,y∈G,于是由条件概率的性质,有
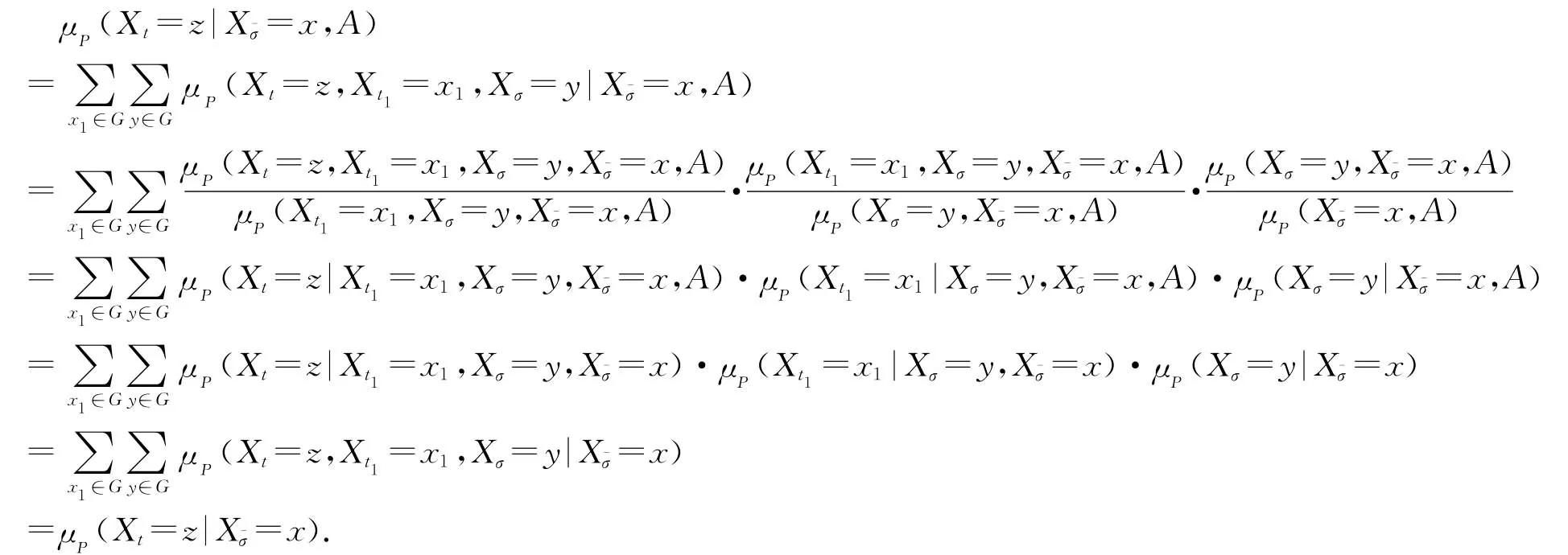
上式第四个等号成立主要是由于定理1的结论而得.所以命题得证.
定理3 设T为一树图,G={0,1,2…}为一可列集合,{Xσ,σ∈T}为取值在G上由定义1定义的树指标马氏链,f是Borel函数,f(Xσ)可积,τi∧σ≤¯σ,1≤i≤n,y∈G,则

[1] Benjamini I.Peres Y.Markov chains indexed by trees[J].Ann Probb,1994,22:219-243.
[2] 杨卫国,刘文.关于齐次树指标可列马氏链的若干极限性质[J].工程数学学报,2004,21(5):769-773.
[3] Spitzer F.Markov random fields on an infinite tree[J].Ann Probab,1975,3:387-398.
[4] Kemeng J G,Snell J L,Knapp A W.Denumberable markov chains[M].New York:Springer,1976:456.
[5] 严加安.测度论讲义[M].北京:科学出版社,2004.
Some Properties for Markov Chains Indexed by a Tree
CHEN Xiao-xue, LI Zeng-tao
(Faculty of Science,Jiangsu University,Zhenjiang 212013,China)
We study some properties for Markov chains indexed by a tree.These properties are similar to the general Markov chains.
Markov chains indexed by a tree;monotone class theorem;conditional probability
O211.6
A
1672-1454(2012)03-0076-04
2009-11-16

