利用渐近展开法求一类多重级数的闭形式

商妮娜， 秦惠增

（山东理工大学理学院，淄博 255049）

利用渐近展开法求一类多重级数的闭形式

商妮娜， 秦惠增

（山东理工大学理学院，淄博 255049）

多重级数；渐近展开；Bernoulli常数；Riemann zeta函数

1 引 言

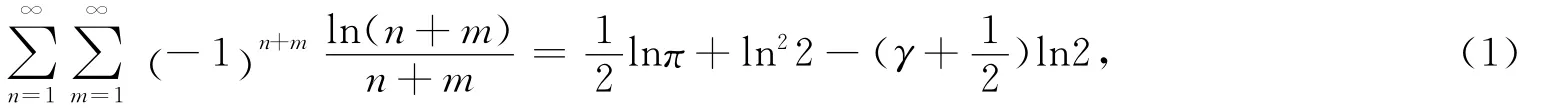
其中γ＝0.57757721566490…是Euler常数.本文考虑相对更复杂的问题，即将（1）推广成下面的多重级数

这里k＝2，3，….我们考虑这个多重级数的闭形式.

2 引理和定理

首先给出下面重要的引理.

引理1［2］设a，n是整数且0≤a＜n.如果f（z）在区域S＝｛z｜a≤Rez≤n｝内是亚纯的且f（z）＝o（e2π｜lnz｜），Imz→±∞在S内一致成立，那么

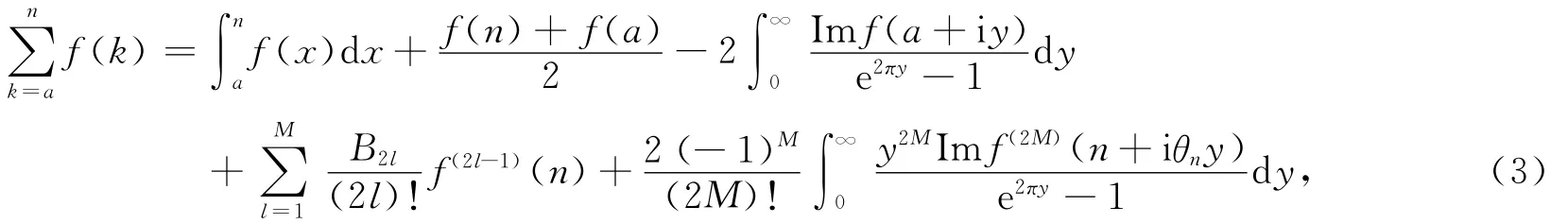
其中Bj是Bernoulli常数，M是一个正整数且0＜θn＜1.

利用数学归纳法很容易证明下面的引理.

引理2对于整数i＞1，则有

引理3对于任意整数m＞0，有

可知（7）成立. 同理可证（5），（6）也成立.

从引理3可得如下结果

并且利用上面的引理就可以得到下面的定理.

定理对于整数k＝2，3，…，则有

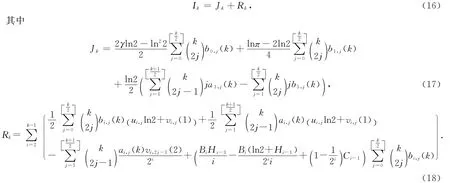
证利用数学归纳法容易证明

［1］Ovidiu Furdui and Qin Huizeng.Solution of problema 149［J］.La Gaceta de la RSME，2010，13（1）：78－79.

［2］Olver，Frank W J.Asymptotics and special functions，Massachusetts：A K Peters，63South Ave，Natick，MA 01 760 1997.

Using Asymptotic Expansion Method Seek the Closed Form for a Class of Multiple Series

SHANGNi－na，QINHui－zeng
（Institute of Applied Mathematics，Shandong University of Technology，255049，China）

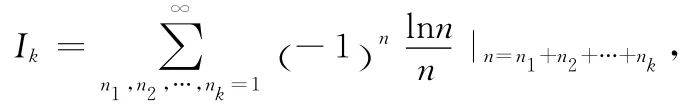
multiple series；asymptotic expansion；Bernoulli constant；Riemann zeta function

O173

A

1672－1454（2012）04－0072－04

2010－03－22