关于一道考研数学试题

程海来

（合肥工业大学数学学院，合肥 230009）

关于一道考研数学试题

程海来

（合肥工业大学数学学院，合肥 230009）

针对2011年全国硕士研究生入学考试的一道试题，从问题的多种解法，问题的推广，相关结论的应用等多个方位进行了讨论，展现了数学发散思维的过程.

函数不等式；一题多解；应用及推广；考研试题

2011年全国硕士研究生入学考试数学（一）、（二）有这样一道试题：

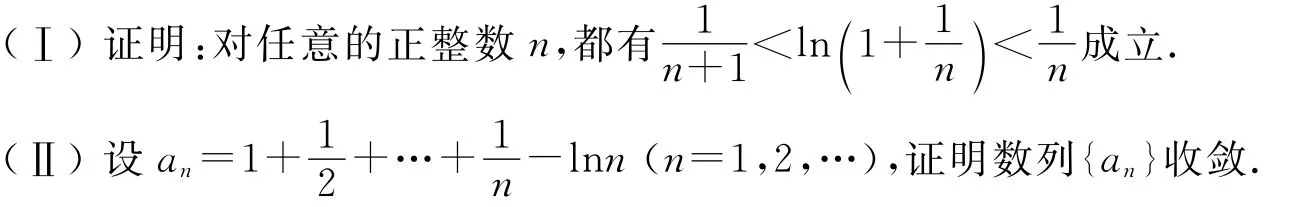
这道试题是一道陈题，不少教材或参考书均可找到，例如［1－3］.本文将围绕这道试题谈几个相关问题：试题的多种解法、问题的推广、数列｛an｝的收敛速度及相关结论的应用.这些内容展现了数学发散思维的一个过程，在教学中若能给学生讲授这一典型案例，这对开拓学生的视野，引导学生不断探索，培养学生的创新意识应该是大有益处的.

1 问题（Ⅱ）的多种解法

这道试题的主要目的是证明（Ⅱ），而问题（Ⅰ）是为了证明（Ⅱ）所设的台阶，所以我们重点讨论（Ⅱ）的不同解法.

解法1利用拉格朗日中值定理可证（Ⅰ），过程从略.

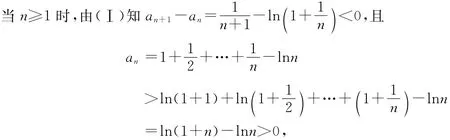
所以数列｛an｝单调下降且有下界，故数列｛an｝收敛.

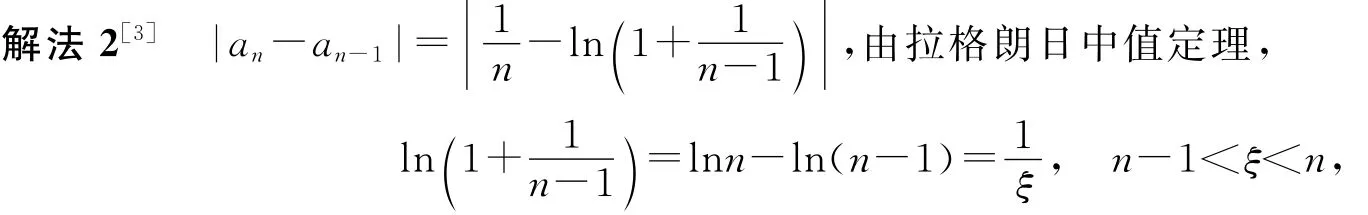
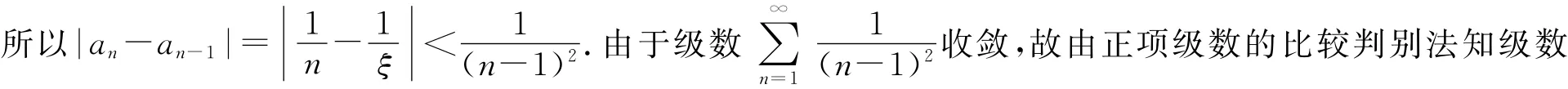
2 问题的推广

问题（Ⅱ）的一般性结论为如下的

命题［4］设f（x）是［0，＋∞）上单调减少且非负的连续函数，

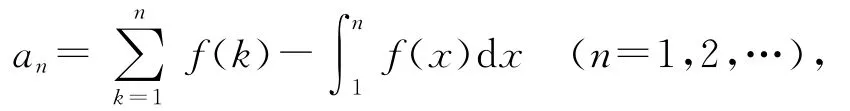
则数列｛an｝的极限存在.（1999年全国硕士研究生入学试题）

证由题设可得

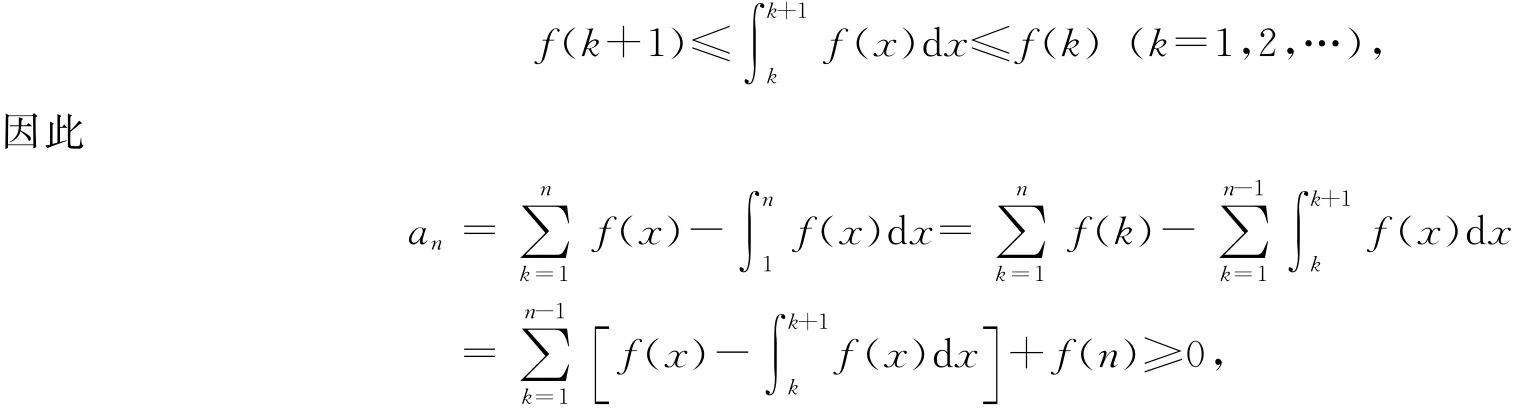
即数列｛an｝有下界.又

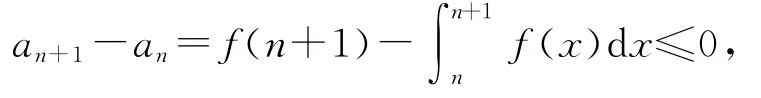
即数列｛an｝单调下降.故由单调有界数列必有极限的准则知数列｛an｝的极限存在.

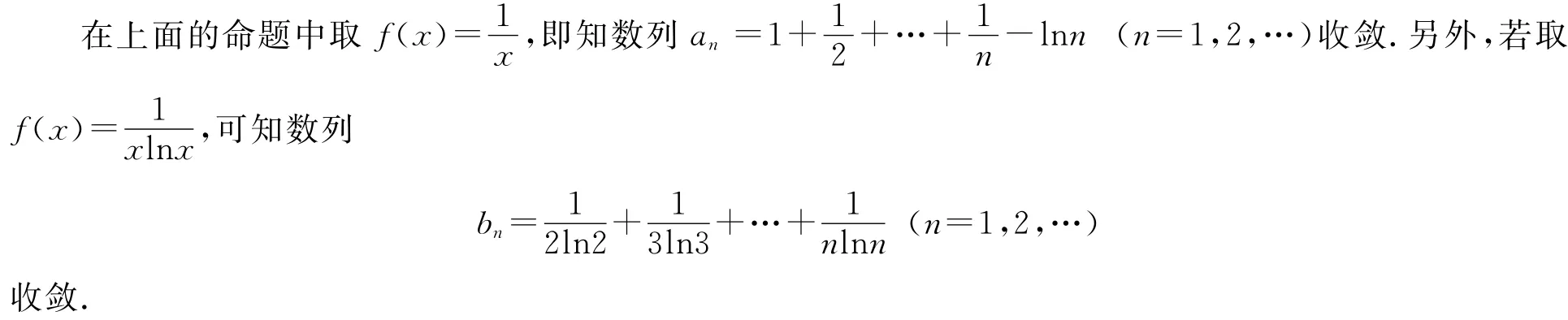
3 数列｛an｝的收敛速度

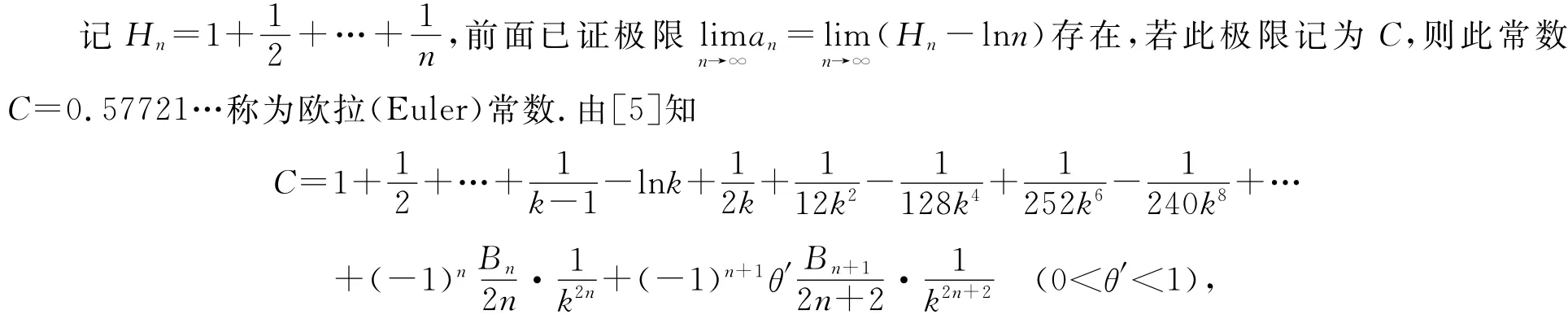
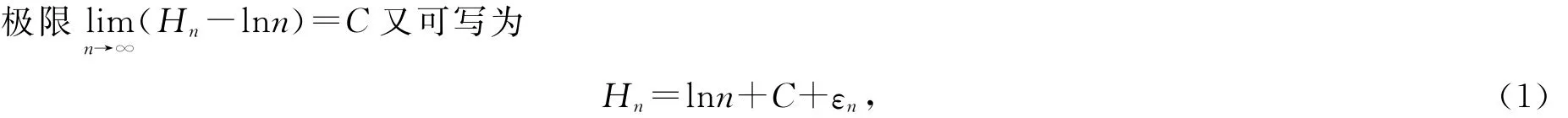
其中εn→0（n→∞）.

（1）式可用来求解某些微积分问题，下面介绍几个相对简单的例子：

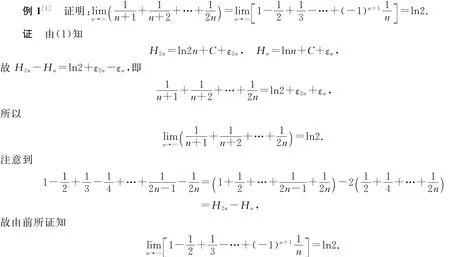
注 利用（1）可得更一般的结果：若m为自然数，则有

（1）式应用的更多例子可参见［6］.

［1］陈纪修，於崇华，金路.数学分析（上册）［M］.2版.北京：高等教育出版社，2004：59－60.

［2］吴良森，毛羽辉，宋国栋，等.数学分析习题精解（单变量部分）［M］.北京：科学出版社，2002：32.

［3］裴礼文.数学分析中的典型问题与方法［M］.2版.北京：高等教育出版社，2007：25，49.

［4］《大学数学》编辑部.硕士研究生入学考试数学试题精解［M］.合肥：合肥工业大学出版社，2010：101.

［5］菲赫金哥尔茨ГМ.微积分学教程（第二卷第三部分）［M］.徐献瑜，冷生明，莫文骐，等译.北京：人民教育出版社，1954：722.

［6］孙本旺，汪浩.数学分析中的典型例题和解题方法［M］.长沙：湖南科学技术出版社，1981：154－169.

O172.1

C

1672－1454（2012）04－0129－04

2011－07－19