讲授Riesz表示定理的两点注记

粟塔山

（国防科技大学理学院，长沙 410073）

讲授Riesz表示定理的两点注记

粟塔山

（国防科技大学理学院，长沙 410073）

对讲授Riesz表示定理提出了两点可供参考的资料和建议.

Riesz表示定理；超平面

笔者近年为工科硕士生讲授《应用数学基础》课程，使用的教材是《应用数学基础》（吴翊，李超，罗建书，戴清平编著，高等教育出版社，2006）.讲到Riesz表示定理时，笔者围绕该定理作了一点铺垫和引申，这对于学生更细致地理解Hilbert空间可能有些益处.

1 Riesz表示定理的一点铺垫

Riesz表示定理的关键结论是：对于Hilbert空间X上的任何线性有界泛函f，存在对应的元素y∈X，使得

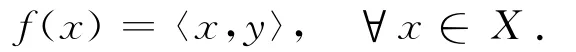
称y为f的表示.教材给出的证明是简洁而清晰的：当f＝0，取y＝0即可；当f≠0，则f的核N（f）≠X，从而N⊥（f）≠0，于是可取到y0∈N⊥（f），y0≠0.作

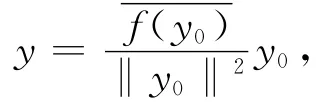
验证即得.第一次讲授时，有学生提问：怎么想到要这样选取y呢？笔者当时没能回答.

教材毕竟不是教案，也许教师的课堂讲授应该说出教材没有说出的话.笔者感觉，如果在Riesz表示定理之前做一些适当的铺垫，就能让学生更轻松地接受定理的证明.于是，笔者第二年讲授该定理时，先补充了一个结论（此前，教材中已经讲述了投影定理）.

引理 设f是Hilbert空间X上的线性有界泛函，且f≠0，那么，N（f）与X只差1维，即存在y0∈N⊥（f），y0≠0，使得

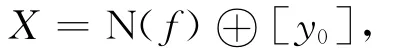
其中［y0］表示y0的张成子空间表示正交和.

证 由f的线性连续性易知N（f）是X的闭子空间.又因为f≠0，即N（f）≠X，故存在y∈X，y∉N（f），取

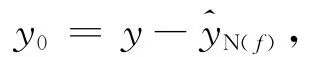
其中是y在N（f）中的投影，从而y0∈N⊥（f），y0≠0.现在∀x∈X，

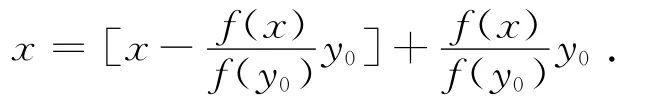
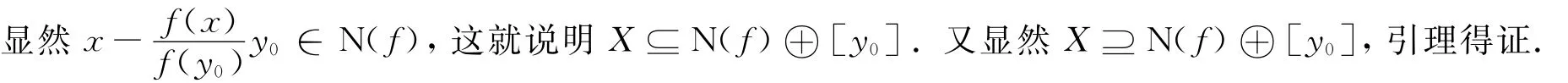
有了这个引理，再来考察对于给定的线性连续泛函f，如何找到y，使得

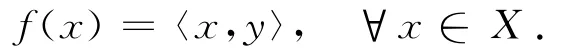
首先注意到，当x∈N（f）时，上式左边为零，故必须y∈N⊥（f）.而根据引理，N⊥（f）是y0张成的一维子空间，所以y必然形如y＝λy0，再如下确定λ：

当f（x）≠0时，欲使得

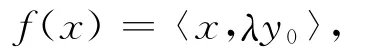
等式右边改写为

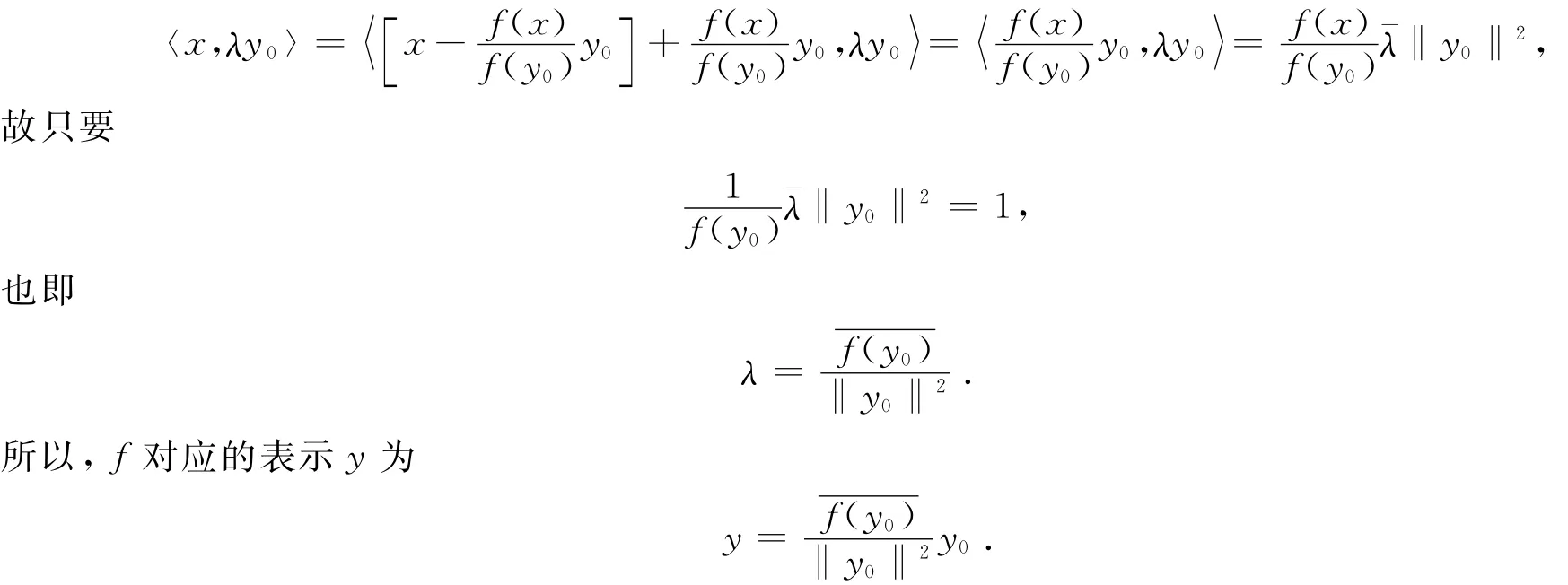
这样，学生对y的来龙去脉有了比较清晰的理解.

2 Riesz表示定理的一点引申

为了更细致地理解Riesz表示定理，对比Rn中过原点的超平面

π是Rn中的n－1维子空间，与Rn只差1维，这个性质与N（f）类似.所以，也可以把N（f）看成X中的超平面.还注意到f的表示y使得

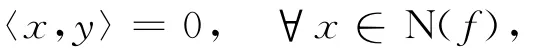
即y可以看成超平面N（f）的法向，它相当于π的法向量a＝（a1，a2，…，an）T.

设fi（i＝1，…，r）是X上r个线性连续泛函，称

为齐次线性方程组.如果fi对应的表示为yi，则方程组可以写作

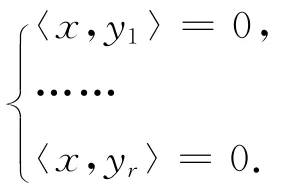
显然该齐次方程组的通解是X的子空间

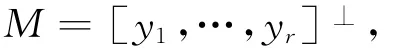
这里［y1，…，yr］表示由y1，…，yr张成的子空间.

对非零常数c，｛x∈X｜f（x）＝c｝是不过原点的超平面（不再是子空间），它是一个仿射集（集合中任意两点的连线属于该集合）.类似地，称（当c1，…，cr不全为零）

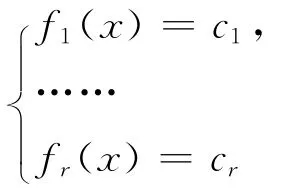
为非齐次方程组.由Riesz表示定理，该方程组也可写作

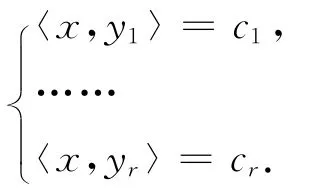
我们有与有限维空间同样的结论，即非齐方程组的通解等于一个特解加上齐方程组的通解.

命题设

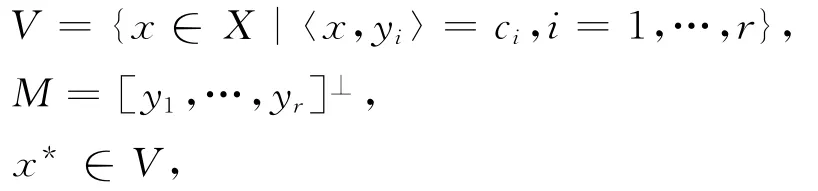
那么，V＝x＊＋M.

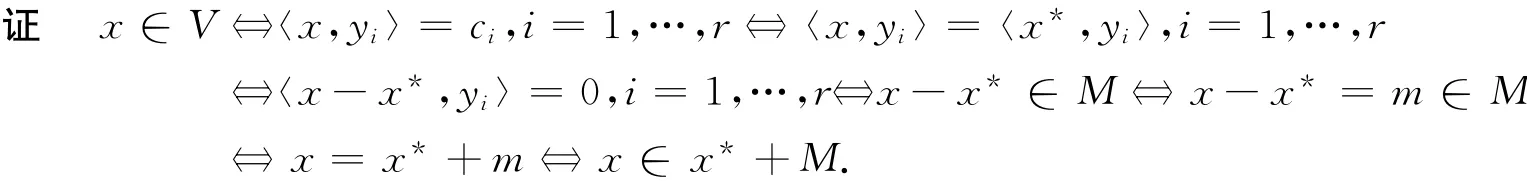
3 结 论

上述内容使得学生对Riesz表示定理有了更细致的理解，也初步认识了无穷维空间中的线性方程组.这些内容对工科硕士生都是容易接受的.为此花费的时间至多1学时.

［1］吴翊，李超，罗建书，戴清平.应用数学基础［M］.北京：高等教育出版社，2006.

［2］Luenberger D G.最优化的矢量空间方法［M］.北京：国防工业出版社，1987.

O177.1

C

1672－1454（2012）04－0133－03

2010－03－08