图Gn的优美表示

吴建强

（广东工业大学华立学院计算机工程系，广东增城 511325）

图Gn的优美表示

吴建强

（广东工业大学华立学院计算机工程系，广东增城 511325）

将给出三个结果：（i）如果图G是上的整数和图，那么0∈S当且仅当图G至少有一个（n－1）度顶点；（ii）图G（G≠K2）是至少有两个零点的整数和图当且仅当G≅K2·Gn；（iii）设图G（G≠K2）是S⊂Z上的整数和图.若图G至少有两个零点，则

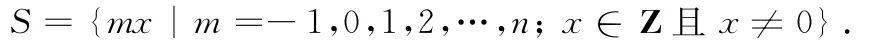
整数和图；零点；图Gn的优美表示；图k2·Gn

在论文［1］中，Frank Harary给出了如下两个定义：

定义1设Z是整数集，S⊂Z，S上的整数和图是图G＝〈V，E〉，其中V＝S，且对于任意的u，v∈S，有uv∈E当且仅当u＋v∈S.

定义2如果图G与S（S⊂Z）上的整数和图同构，则称图G是整数和图.

设Nn＝｛1，2，…，n｝，将Nn上的整数和图记为Gn［1］.由完全图K2

［2］的两个顶点与Gn的每个顶点邻接所构成的图记为K2·Gn.图G5与K2·G5如图1与图2所示.另外，约定Z表示整数集，Z＊表示非零整数集，N表示自然数集，N＋表示正整数集.本文所讨论的图均为有限简单图［2］.

图1 图G5

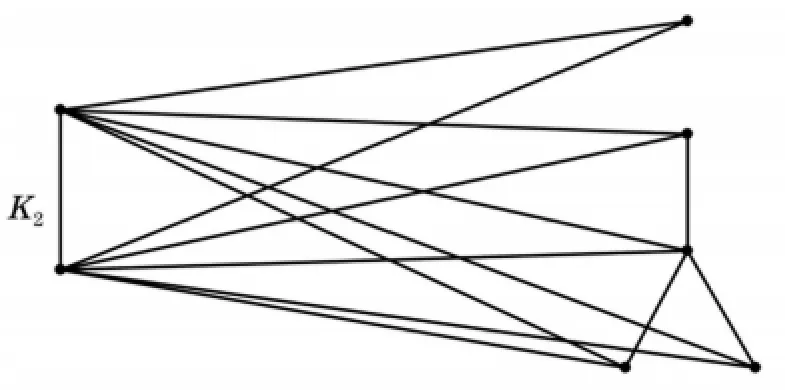
图2 图K2·G5

定理1设图G是S⊂上的整数和图，则0∈S当且仅当图G至少有一个（n－1）度顶点.

证设V（G）＝｛vi｜i＝1，2，…，n｝，S＝｛si｜i＝1，2，…，n｝，且vi＝si（即顶点vi的标号是si），i＝1，2，…，n.

必要性.如果0∈S，则存在某个正整数a，1≤a≤n，使得sa＝0.显然，有sa＋si＝0＋si＝si∈S（i＝1，2，…，a－1，a＋1，…，n），又已知图G是S上的整数和图，则由定义1可知，vavi∈E（G）（i＝1，2，…，a－1，a＋1，…，n），即degva＝n－1，因此图G至少有一个（n－1）度顶点.

充分性.如果图G至少有一个（n－1）度顶点，则存在某个正整数a，1≤a≤n，使得degva＝n－1，即vavi∈E（G），i＝1，2，…，a－1，a＋1，…，n.已知图G是S上的整数和图，根据定义1，有

此时，如果0∉S，即si≠0（i＝1，2，…，n），则用数学归纳法可以证明：对于任意自然数m，都有

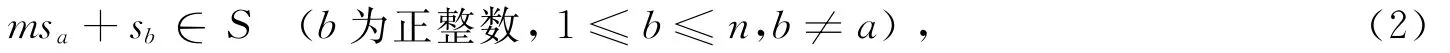
从而有｛msa＋sb｜m∈N｝⊆S.这与S是有限集矛盾，故0∈S.

下面用数学归纳法证明：若0∉S，则（2）式对于任意自然数m都成立.

（i）当m＝0时，（2）式显然成立.由（1）式可知，sa＋sb∈S，即当m＝1时，（2）式也成立.

（ii）假设对任意自然数m，当m＜k（k＞1，k∈N＋）时，（2）式都成立.由此假设可得（k－2）sa＋sb∈S.若（k－1）sa＋sb＝sa，即（k－2）sa＋sb＝0，则有0∈S，这与0∉S矛盾，故（k－1）sa＋sb≠sa.再由假设可得（k－1）sa＋sb∈S，因此存在某个正整数l，l≠a，1≤l≤n，使得（k－1）sa＋sb＝sl，从而由（1）式可知

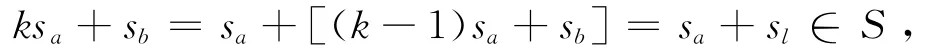
即当m＝k时，（2）式仍成立.

在图G中，若某个顶点与其它顶点均邻接，则称这个顶点为图G的零点.

定理1表明：当图G是整数集S⊂Z＝n≥2）上的整数和图时，若图G有零点，则0∈S，否则0∉S.

设S⊂Z，m∈Z＊，规定mS＝｛mx｜x∈S｝.

引理若图G是S⊂Z上的整数和图，则图G也是mS（m∈Z＊）上的整数和图.

证设S＝｛ai｜i＝1，2，…，n；n∈N＋｝，则mS＝｛mai｜i＝1，2，…，n；n∈N＋｝.在S与mS之间建立如下1－1映射：

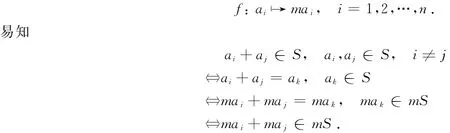
再由定义1可知，S上的整数和图与mS上的整数和图同构［2］，由此得引理.

定理2图G（G≠k2）是至少有两个零点的整数和图当且仅当G≅k2·Gn.

证充分性.若图G≅k2·Gn，则由定义1可知，图G是数集｛－1，0，1，2，…，n｝上的整数和图，且至少有两个零点（标号为0及－1的两个顶点都是零点）.

必要性.假设图G（G≠k2）是至少有两个零点的整数和图，根据定义2，可设图G是S⊂Z上的整数和图，其中S＝｛si∈Z｜i＝1，2，…，n＋2｝，V（G）＝｛｜i＝1，2，…，n＋2｝且表示标号为si的顶点.据定理1可知，0∈S，因而图G的零点中有一个标号是0.将另外一个零点的标号设为x（x∈S，x≠0）.对于任意的t∈S，t≠x，显然有vxvt∈E（G），则由定义1得

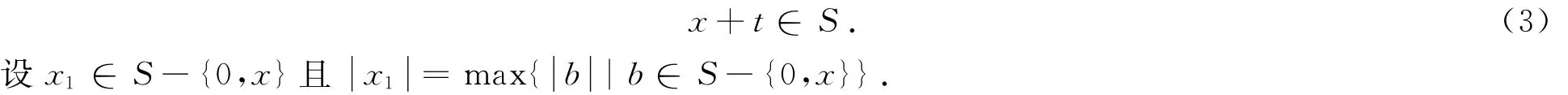
为了确定整数集S，首先，用反证法证明：对于任意一个a∈S－｛0，x｝，存在一个相应的正整数m0，使得m0x＋a＝0，即

假设对于任意的m∈N＋，都有

则用数学归纳法可以证明：对于任意正整数m，都有

从而有｛mx＋a｜m∈N＋｝⊆S，这与S是有限集矛盾.

下面用数学归纳法证明：若（5）式对于任意正整数m都成立，则（6）式对于任意正整数m也都成立.

（i）由（3）式可知x＋a∈S，即当m＝1时，（6）式成立.

（ii）假设当m＝k（k∈N＋）时，（6）式成立，即kx＋a∈S.据（5）式及a∈S－｛0，x｝，易知对任意的k∈N＋，有（k－1）x＋a≠0，即kx＋a≠x，从而由（3）式可得

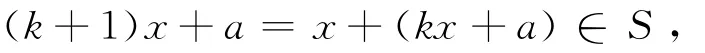
即当m＝k＋1时，（6）式仍成立.

在（4）式中，若a＝x1，则可设m0＝m1，即x1＝－m1x.

其次，用数学归纳法可以证明：对于任意的m∈｛1，2，…，m1－1，m1｝，有

（i）由（3）式可知，x＋x1∈S，即当m＝1时，（7）式成立.

（ii）假设当m＝k（k＜m1）时，（7）式成立，即kx＋x1∈S.由x1＝－m1x，有

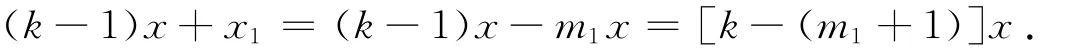
因为k＜m1，x≠0，所以［k－（m1＋1）］x≠0，即kx＋x1≠x.于是由（3）式可得

即当m＝k＋1时，（7）式仍成立.

再次，确定整数集S.构造集合A＝｛0，x，x1，x＋x1，2x＋x1，…，（m1－1）x＋x1｝.由（7）式可知，A⊆S.事实上A＝S，否则假设A⊂S，即存在x2∈S，x2∉A.由（4）式可知，存在m2∈N＋，使得x2＝－m2x.因为A＝｛0，x，－m1x，－（m1－1）x，…，－x｝（由x1＝－m1x得到）且x2∉A，所以m2＞m1，从而有

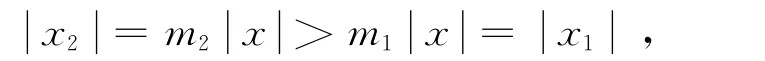
这与x1是S－｛0，x｝中绝对值最大的整数矛盾.于是，由A＝S可，因而m1＝n，所以

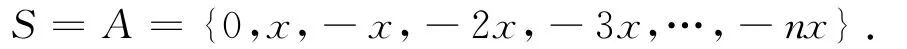
图K2·Gn是整数集S′＝｛－1，0，1，2，…，n｝上的整数和图（由定义1可知）且S＝－xS′，x∈Z＊，据引理可得，图K2·Gn也是S上的整数和图，而据前面的假设，图G是整数集S上的整数和图，故图G≅K2·Gn.

定理1给出了图Gn的一条重要性质，也给出了图Gn结构的一个优美表示［1］.此定理对于研究一般的整数和图很有用.例如，由定理可知，在零点数不小于2的所有非k2图中，只有图k2·Gn才是整数和图，而其余图都不是整数和图.

由定理2的必要性的证明可得：

定理3设图G（G≠k2）是S⊂Z上的整数和图，＝n＋2，n∈N＋.若图G至少有两个零点，则

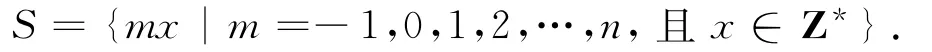
由定理2的充分性的证明可知，图k2·Gn是至少有两个零点的整数和图.假设图k2·Gn是S⊂Z上的整数和图，则根据定理3可以断定

［1］Frank Harary.Sum graphs over all the integers［J］.Discrete Mathematics，1994，124：99—105.

［2］Bondy J A，Murty U S R.Graph theory with applications［M］.New york：Macmillan Press，1976.

［3］哈拉里F.图论［M］.李慰萱译.上海：上海科学技术出版社，1963.

［4］卢开澄，卢华明.图论及其应用［M］.2版.北京：清华大学出版社，1995.

［5］王朝瑞.图论［M］.3版.北京：北京理工大学出版社，2001.

An Elegant Description of GraphGn

WuJian－qiang
（Computer Engineering Department，Guangdong University of Technology Huali College，Zengcheng Guangdong 511325，China）

We will give the following three results：（i）IfG＝＜V，E＞，＝n≥2andGis a sum graph overSthat is an integer set，then 0∈Sif and only if there is a vertexx（x∈V）withdG（x）＝n－1；（ii）The graphG（G≠k2）is an integral sum graph with two or more 0－vertex if and only ifG≅k2·Gn；（iii）Assume a graphGis an integral sum graph overS（S⊂Z），＝n＋2，n∈N＋，If the graphGhas at least two 0－vertex，thenS＝｛mx｜m＝－1，0，1，2，…，n，andx∈Z＊｝.

the integral sum graph；0－vertex；an elegant description of the structure of graphGn；the graphk2·Gn

O15

A

1672－1454（2012）04－0064－04

2009－12－28；［修改日期］2010－05－28