论泰勒中值定理“中间点”的性质

时统业， 谢 井， 李 鼎

（海军指挥学院浦口分院，江苏南京 211800）

论泰勒中值定理“中间点”的性质

时统业， 谢 井， 李 鼎

（海军指挥学院浦口分院，江苏南京 211800）

研究泰勒中值定理“中间点”的单调性、连续性及可导性.

泰勒中值定理；中间点；单调；连续；导数

1 前 言

文［1］研究了拉格朗日中值定理“中间点”ξ的单调性、连续性及可导性问题.本文利用文［1］的方法，研究泰勒中值定理“中间点”ξ的单调性、连续性及可导性问题，推广了文［1］的部分结果.

2 引 理

引理1（拉格朗日中值定理） 设函数f（x）在［a，b］上连续，在（a，b）内可导，则对任意x∈（a，b］，至少存在一点ξ∈（a，x），使

引理2（泰勒中值定理） 设函数f（x）在［a，b］上有直到n＋1阶导数，则对任意x∈（a，b］，至少存在一点ξ∈（a，x），使

定义1对于在［a，b］上有直到k阶导数的函数h（x），记关于x的一元函数（k仅看作参数）

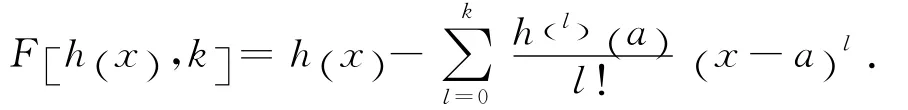
由（2）式得

n

引理3对任意正整数k，有

引理4设函数f（x）在［a，b］上有直到n＋1阶导数，记

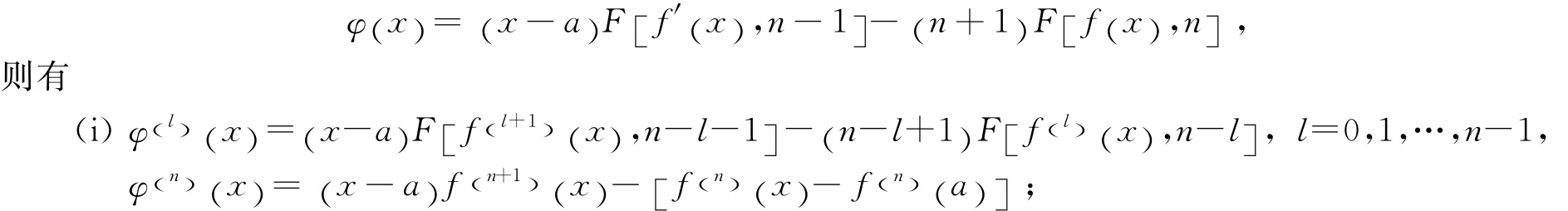
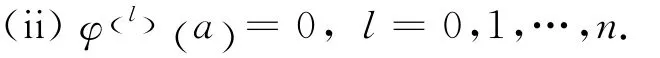
证 （i）l＝0时，由定义，（i）显然成立.假设对某个自然数l＝m：0≤m≤n－2，有

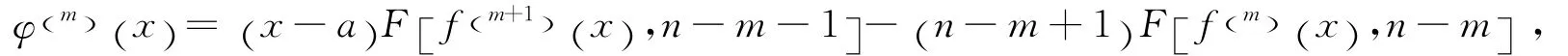
对上式关于x求导并利用引理3，得

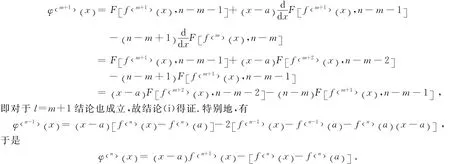
（ii）由定义1和结论（i）容易得证.

引理5［1］设f（x）在［a，b］上连续，在（a，b）内可导，且f′（x）在（a，b）内严格单调，那么

（i）满足（1）式的ξ是x的单值函数，记为ξ＝ξ（x）；

（ii）满足（1）式的点ξ＝ξ（x）是x的单调增加的函数.

引理6［1］设函数f（x）在［a，b］上连续，在（a，b）内二阶可导，且二阶导数在（a，b）内保号（恒正或恒负），则

（i）满足（1）式的点ξ＝ξ（x）是x的连续函数；

（ii）满足（1）式的点ξ＝ξ（x）是x的可导函数，其导数为

3 结 论

定理1设函数f（x）在［a，b］上有直到n＋1阶导数，且f（n＋1）（x）在（a，b）内严格单调，则

（i）满足（2）式的点ξ是x的单值函数，记为ξ＝ξ（x）；

（ii）满足（2）式的点ξ是x单调增加的函数.

证 结论（i）可由f（n＋1）（x）的单调性立得.下面证明结论（ii）.当n＝0时，由引理5知结论成立.当n≥1时，不妨假设f（n＋1）（x）在（a，b）内严格单调增加，f（n＋1）（x）严格单调减少时类似可证.设

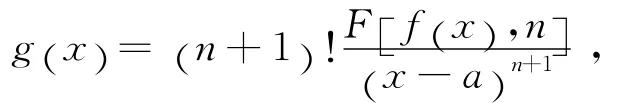
如果证得g（x）单调增加，则对于任意x1，x2∈（a，b］，就有g（x1）＜g（x2），由（3）式即有f（n＋1）（ξ（x1））＜f（n＋1）（ξ（x2））.由于f（n＋1）（x）在（a，b）内严格单调增加，故ξ（x1）＜ξ（x2）.

为了证明g（x）单调增加，只要证明g′（x）＞0.

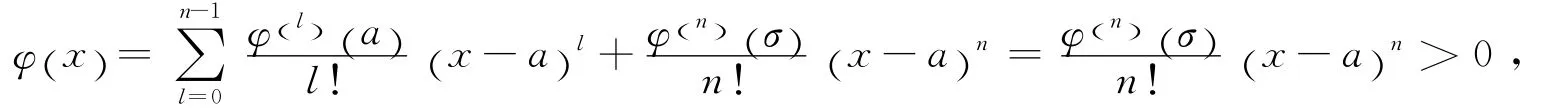
其中σ∈（a，x），从而g′（x）＞0，结论（ii）得证.

定理2设函数f（x）在［a，b］上有直到n＋2阶连续导数，且f（n＋2）（x）在（a，b）内不变号，函数ξ＝ξ（x）满足（2）式，则

［1］刘龙章，戴立辉，杨志辉.再论微分中值定理“中间点”的性质［J］.大学数学，2007，23（4）：163－165.

［2］同济大学数学教研室.高等数学（上册）［M］.4版.北京：高等教育出版社，1996：173－174.

［3］裴礼文.数学分析中的典型问题与方法［M］.北京：高等教育出版社，2007：229－230.

Disscussion of the Properties of the Intermediate Point in Taylor Mean－Value Theorem

SHITong－ye，XIEJing，LIDing
（Pukou Institute of Naval Command College，Nanjing 211800，China）

We give properties of the intermediate point in Taylor mean－value theorem，such as monotony，continuous，derivative.

Taylor mean－value theorem；intermediate point；monotony；continuous；derivative

O172.1

C

1672－1454（2012）04－0120－04

2010－09－03