随机奇异积分的Привалов－Plemelj公式

李 蔚， 殷承元

（1.安徽省邮电职业技术学院，合肥 230031； 2.上海财经大学，上海 200433）

随机奇异积分的Привалов－Plemelj公式

李 蔚1， 殷承元2

（1.安徽省邮电职业技术学院，合肥 230031； 2.上海财经大学，上海 200433）

在概率极限意义下，研究了随机奇异积分，得到了Привалов－Plemelj公式，并获得了有关随机奇异积分的性质，取得了一些有意义的成果.

随机奇异积分；Привалов－Plemelj公式；概率极限

复变函数的奇异积分于上个世纪上半叶蓬勃发展而起的，其代表人物有 МУсхелишвили［1］，Привалов［2］，并在弹性力学的研究方面具有极大的推动作用.随后进入了国内，有许多数学家在此做了大量的开创性的工作.数学家路见可先生提出了复变函数的Riemann边值问题以及周期问题，奇异积分方程的直接解法，且极其巧妙地处理了有关的平面弹性力学问题［3，4］.杜金元教授在奇异积分的计算方面作了卓有成效的工作，有效的解决了奇异积分许多问题［5］.著名数学家龚升先生开创了多复变函数上典型域上的奇异积分［6］.1954年著名数学家陆启铿院士和钟同德教授的“普列瓦洛夫定理的推广”受到了李国平院士和当时的苏联加霍夫（Гахов）学派称赞，认为这是创新工作，给予颇高评价.当然，还有许许多多的国内外的专家和学者从事着这个领域的工作.

本文将尝试着对含有随机量的奇异积分，在概率极限意义下，进行探讨，取得一些有意义的结果.

设G是复平面中的非空集合，Ω是样本空间，（Ω，A，P）是概率测度空间，x（t，w）是一个G×Ω上的函数.对任意一个t∈G，x（t，w）是Ω上的随机变量，即是（Ω，A，P）上的可测函数.换句话说，x（t，w）是以G为指标集的Ω上的随机过程.

定义1设x（t，w）是以G为指标集的Ω上的随机过程.如果对任一t∈G，都有E（｜x（t，w）｜2）＜＋∞，称x（t，w）为平方可积的，记为

定义3设x（t，w）是以G为指标集的Ω上的随机过程.如果对任t∈G，s∈G，存在常数A＞0和α∈（0，1］，使得，那么称x（t，w）在期望意义下是具有α指数的Hölder连续的，简称为Hölder连续.记Hα（G；Ω，A，P）为所有确定的G，（Ω，A，P）具有α指数的Hölder连续的集合.

对任一x（t，w）∈Hα（G；Ω，A，P），定义

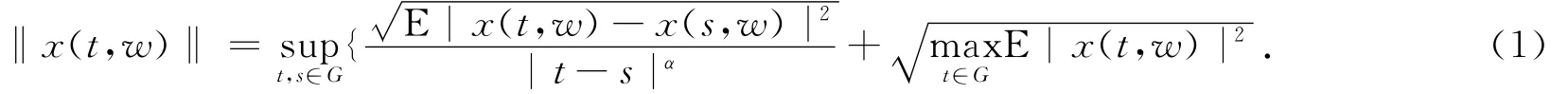
证Hα（G；Ω，A，P）是一个线性空间是显然的.下证‖x（t，w）‖满足范数的条件.

［1］МусхелищвилНИ.奇异积分方程 ：函数论边值问题及其在数学物理中的某些应用［M］.朱季讷译.上海：科学技术出版社，1966.

［2］ПриваловИИ.复变函数引论［M］.闵嗣鹤，等译.北京：人民教育出版社，1956.

［3］路见可.解析函数边值问题［M］.上海：上海科学技术出版社，1987.

［4］路见可.平面弹性复变方法［M］.3版.武汉：武汉大学出版社，2005.

［5］Du Jinyuan.Singular integral operators and singular quadrature operators associated with singular integral equations［J］.Acta.Math.Sci.，1998，18（2）：227－240.

［6］龚升.多复变数的奇异积分［M］.上海：上海科学技术出版社，1982，

［7］陆启铿.多复变函数论的回顾与前瞻［J］.首都师范大学学报（自然科学版），1996，17（4）：1－7.

［8］殷承元.闭复超球上的普里瓦洛夫定理［J］.安徽大学学报（自然科学版），1990，14（3）：6－11.

Привалов－Plemelj’Formula of Stochastic Singular Integral

LIWei1，YINCheng－yuan2
（1.Anhui Post and Communication College，Heifei 230039，China；2.Shanghai University of Finance and Economics，Shanghai 200433，China）

The stochastic singular integral in investigated in the sense of probability，andПривалов－Plemelj’formula is proved，and some properties on the stochastic singular integral are obtained.

stochastic singular integral；Привалов－Plemelj’formula；limit in sense of probability

O175.8；O211.4

A

1672－1454（2012）04－0059－05

2012－02－24；［修改日期］2012－04－24