浅析二次函数在高中阶段的应用

◆史志红

(河北省乐亭第二中学)

浅析二次函数在高中阶段的应用

◆史志红

(河北省乐亭第二中学)

一、进一步深入理解函数概念

初中阶段已经讲述了函数的定义，进入高中后在学习集合的基础上又学习了映射，接着重新学习函数概念，主要是用映射观点来阐明函数，这时就可以用学生已经有一定了解的函数，特别是二次函数为例来加以更深认识函数的概念。二次函数是从一个集合A(定义域)到集合B(值域)上的映射:A→B，使得集合B中的元素y=ax2+bx+c(a≠0)与集合A的元素X对应，记为(x)=ax2+bx+c(a≠0)这里ax2+bx+c表示对应法则，又表示定义域中的元素X在值域中的象，从而使学生对函数的概念有一个较明确的认识，在学生掌握函数值的记号后，可以让学生进一步处理如下问题:

类型Ⅰ:已知(x)=2x2+x+2，求(x+1)

这里不能把(x+1)理解为x=x+1时的函数值，只能理解为自变量为x+1的函数值。

类型Ⅱ:设(x+1)=x2－4x+1，求(x)

这个问题理解为，已知对应法则下，定义域中的元素x+1的象是x2－4x+1，求定义域中元素X的象，其本质是求对应法则。

把所给表达式表示成x+1的多项式。

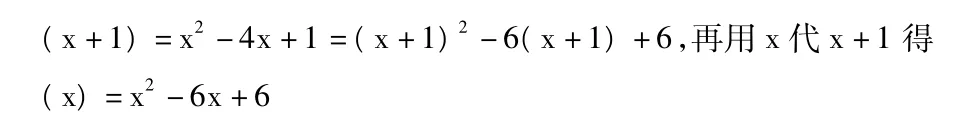
二、二次函数的单调性，最值与图象

在高中阶阶段学习单调性时，必须让学生对二次函数y=ax2+bx+c在区间(－∞，－b/2a］及［－b/2a，+∞)上的单调性的结论用定义进行严格的论证，使它建立在严密理论的基础上，与此同时，进一步充分利用函数图象的直观性，给学生配以适当的练习，使学生逐步自觉地利用图象学习二次函数有关的一些函数单调性。

类型Ⅲ:画出下列函数的图象，并通过图象研究其单调性。

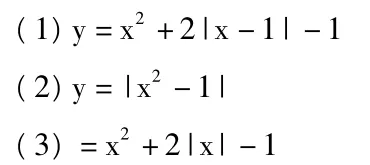
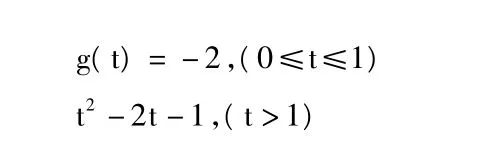
首先要使学生弄清楚题意，一般地，一个二次函数在实数集合R上或是只有最小值或是只有最大值，但当定义域发生变化时，取最大或最小值的情况也随之变化，为了巩固和熟悉这方面知识，可以再给学生补充一些练习。

如:y=3x2－5x+6(－3≤x≤－1)，求该函数的值域。

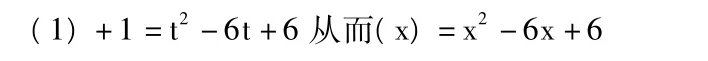
二次函数的知识，可以准确反映学生的数学思维:

类型Ⅴ:设二次函数g(x)=ax2+bx+c(a＞0)方程g(x)－x=0的两个根 X1，X2满足0＜x1＜x2＜1/a.

(Ⅰ)当 X∈(0，x1)时，证明 x＜g(x) ＜x1.

(Ⅱ)设函数g(x)的图象关于直线x=x0对称，证明x0＜x2.

解题思路:

本题要证明的是x＜g(x)，g(x)＜x1和x0＜x2，由题中所提供的信息可以联想到:①g(x)=x，说明抛物线与直线y=x在第一象限内有两个不同的交点;②方程g(x)－x=0可变为ax2+(b－1)x+1=0，它的两根为x1，x2，可得到x1，x2与a、b、c之间的关系式，因此解题思路明显有三条①图象法②利用一元二次方程根与系数关系③利用一元二次方程的求根公式，辅之以不等式的推导。现以思路②为例解决这道题:

(Ⅰ)先证明x＜g(x)，令g(x)=g(x)－x，因为 x1，x2是方程 g(x)－x=0的根，g(x)=ax2+bx+c，所以能 g(x)=a(x－x1)(x－x2)

因为0＜x1＜x2，所以，当 x∈(0，x1)时，x－x1＜0，x－x2＜0得(x－x1)(x－x2)＞0，又 a＞0，因此 g(x)＞0，即 g(x)－x＞0.至此，证得 x＜g(x)

根据韦达定理，有x1x2=ca

∵ 0＜x1＜x2＜1/a，c=ax1x2＜x=g(x1)，又 c=g(0)

∴g(0)＜g(x1)

根据二次函数的性质，曲线y=g(x)是开口向上的抛物线。因此，函数y=g(x)在闭区间［0，x1］上的最大值在边界点x=0或x=x1处达到，而且不可能在区间的内部达到，由于g(x1)＞g(0)，所以当x∈(0，x1)时g(x)＜g(x1)=x1，

即x＜g(x)＜x1

(Ⅱ)略

二次函数，它有丰富的内涵和外延。作为最基本的幂函数，可以以它为代表来研究函数的性质，可以建立起函数、方程、不等式之间的联系，可以偏拟出层出不穷、灵活多变的数学问题，考查学生的数学基础知识和综合数学素质，特别是能从解答的深入程度中，区分出学生运用数学知识和思想方法解决数学问题的能力。