一类链图的优美性

吴丽鸿，王世英

(1.山西电力职业技术学院基础部，太原 030021;2.山西大学数学科学学院，太原 030006)

1 定义

优美图是图论中的重要课题，但至今由于缺乏一般性的研究手段，寻找具有优美性的图类仍是这个领域内目前的研究重点。本文讨论的图G(V，E)均为无向简单图，其中V(G)和E(G)分别表示图G(V，E)的顶点集和边集，|E(G)|表示图G(V，E)的边数，未说明的符号及术语见参考文献[1]。

定义1[1]若一个图的顶点集可以分解为两个(非空)子集X和Y，使得每条边都有一个端点在X中，另一个端点在Y中，这样的一个图称为二部图(或偶图);这样的一种分类(X，Y)称为二分类;若X的每个顶点都和Y中的每个顶点相连，称为一个完全二部图;若|X|=m，而|X|=n，这样的完全二部图记为 Km，n.

定义2[2]一个q条边的简单图G(V，E)，如果存在一个单射 f∶V(G)→ {0，1，2，…，q}，使得对所有的e=(u，v)，由f'(e)=|f(u)－f(v)|导出的E(G)→ {1，2，…，q}是一个双射，则称图 G(V，E)是优美图，f是图G(V，E)的优美标号(或优美值)。

定义3 设k个完全二部图k2，mi，对应的二分类为(Xi，Yi)，且 |Xi|=2，|Yi|=mi，其中mi为大于1 的正整数，i=1，2，…，k.将 Yi中的两个点分别定义为前点和后点。将Xi中两个点分别定义为起点和终点。

定义4 由 k 个完全二部图 K2，m1，K2，m2，…，K2，mk的前点和后点依次粘接而成的图称为链图T1.

定义5 由 k 个完全二部图 K2，m1，K2，m2，…，K2，mk的起点和终点依次粘接而成的图称为链图T2.

定义6 由链图T1中Yk的后点与长为n的路Pn的一个端点粘接得到的图称为链图T3.

定义7 由链图T2中Yk的终点与长为n的路Pn的一个端点粘接得到的图称为链图T4.

定义8 设 k 个完全二部图 K2，m1，K2，m2，…，K2，mk，将 K2，mi的终点和 K2，mi+1的前点粘接得到的图记为其中 i=1，3，5，…，k － 1，将，的起点和后点依次粘接而成的图称为链图T5.

定理 1[3]对于自然数 n，连通图 T(Fn，4，Pm)是优美图。

定理2[3]对于自然数n，连通图Fn，4是优美图。本文将文献[3]的定理4和定理5的条件范围加以扩大，得到了一些优美图。文献[3]-文献[11]均对一些图进行了优美性研究。

2 主要结果及其证明

定理3 对于大于1的正整数 k，m1，m2，…，mk，图T1是优美图。

证明 设图T1顶点和边如图1所示。

下面给出图T1的标号f(v):

设m=m1+ … +mk，

f(U0)=0，

f(Ui)=m1+ … +mi+i，(i=1，2，…，k －1)，

f(Vi)=2m － i+1，(i=1，2，…，m － k+1)，

f(Wi)=m1+ … +mi+i－1，(i=1，2，…，k).

易证得f(v)是图T1的优美标号。

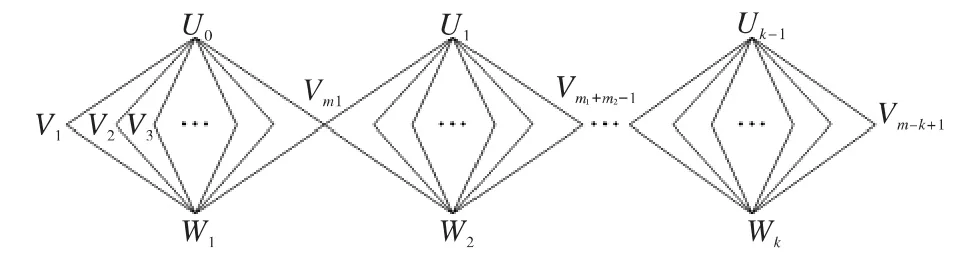
图1 链图T1Fig.1 Chain graph T1

定理4 对于大于1的正整数 k，m1，m2，…，mk，图T2是优美图。

证明 设图T2的顶点和边如图2所示。

下面给出图T2的标号f(v):

设m=m1+ … +mk，

f(V0)=0，

f(Ui)=2m+1 － i，(i=1，2，…，m)，

f(Vi)=m1+ … +mi，(i=1，2，…，k).

易证得f(v)是图T2的优美标号。

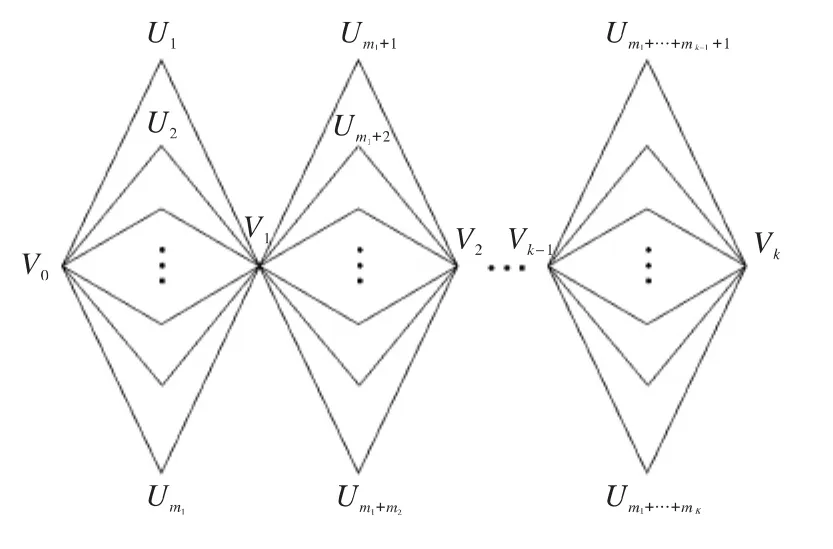
图2 链图T2Fig.2 Chain graph T2

定理5 对于大于1的正整数 k，m1，m2，…，mk，正整数n，图T3是优美图。

证明 设图T3的顶点和边如图3(n为偶数)和图4(n为奇数)所示。

下面给出图T3的标号f(v):

设m=m1+… +mk，

f(U0)=0，

f(Ui)=m1+ … +mi+i，(i=1，2，…，k －1)，

f(Vi)=2m+n － i+1，(i=1，2，…，m － k+1)，

f(Wi)=m1+ … +mi+i－1，(i=1，2，…，k).

当n为偶数时，

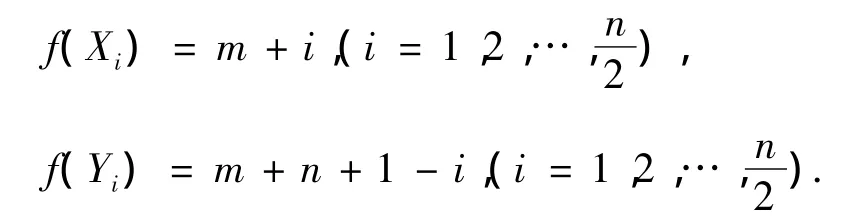
当n为奇数时，

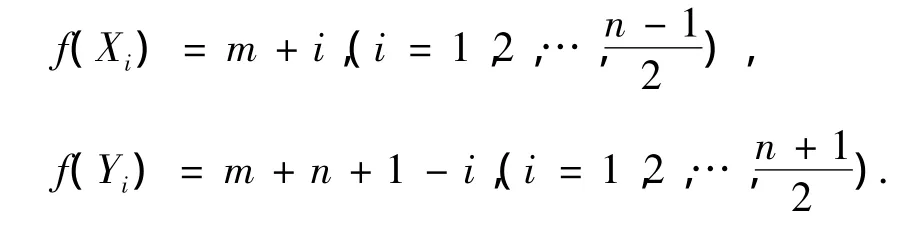
易证得f(v)是图T3的优美标号。

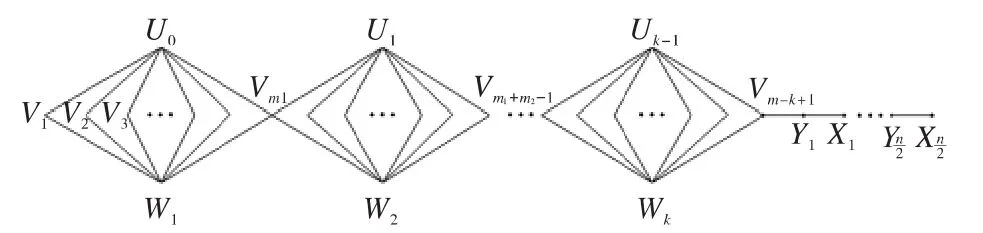
图3 链图T3，n为偶数Fig.3 Chain graph T3

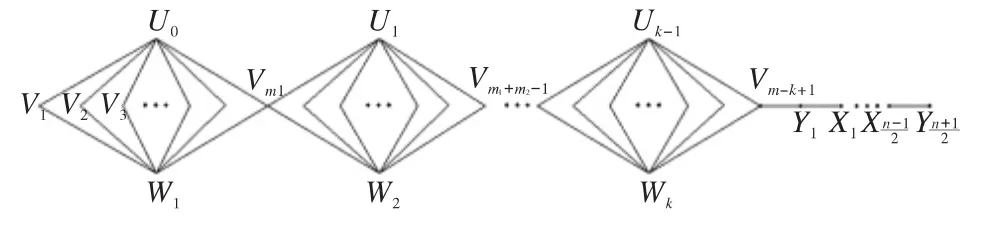
图4 链图T3，n为奇数Fig.4 Chain graph T3

定理6 对于大于1的正整数 k，m1，m2，…，mk，正整数n，图T4是优美图。

证明 设图T4的顶点和边如图5(n为偶数)和图6(n为奇数)所示。

下面给出图T4的标号f(v):

设m=m1+… +mk，

f(Ui)=2m+n+1 － i，(i=1，2，…，m)，

f(V0)=0，

f(Vi)=m1+ … +mi，(i=1，2，…，k).

当n为偶数时，

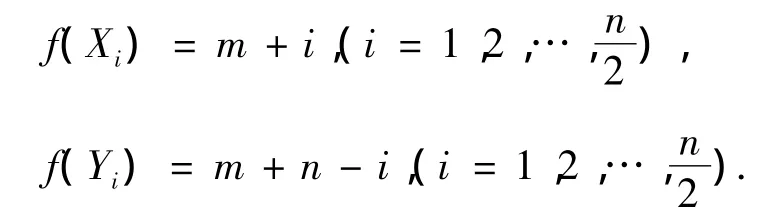
当n为奇数时，

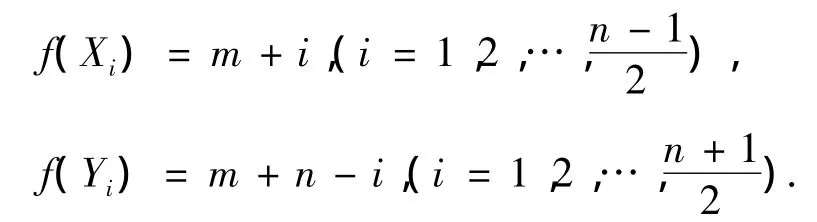
易证得f(v)是图T4的优美标号。

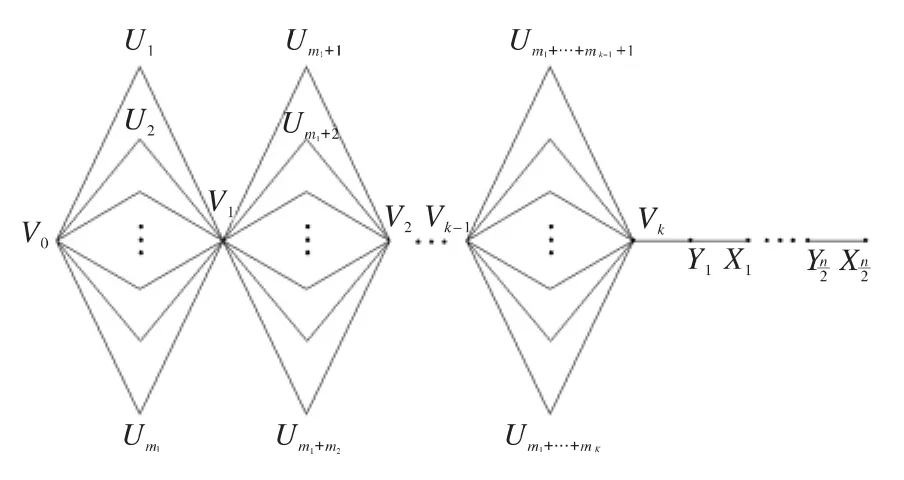
图5 链图T4，n为偶数Fig.5 Chain graph T4

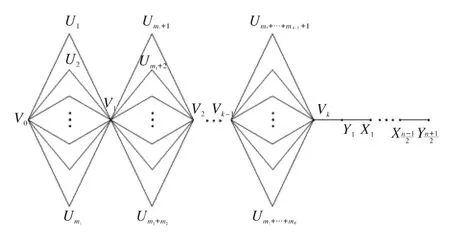
图6 链图T4，n为奇数Fig.6 Chain graph T4

定理7 对于大于1的正整数k，m1，m2，…，mk和正整数n，图T5是优美图。

证明 设图T5的顶点和边如图7所示。

下面给出图T5的标号f(v):

设m=m1+… +mk，

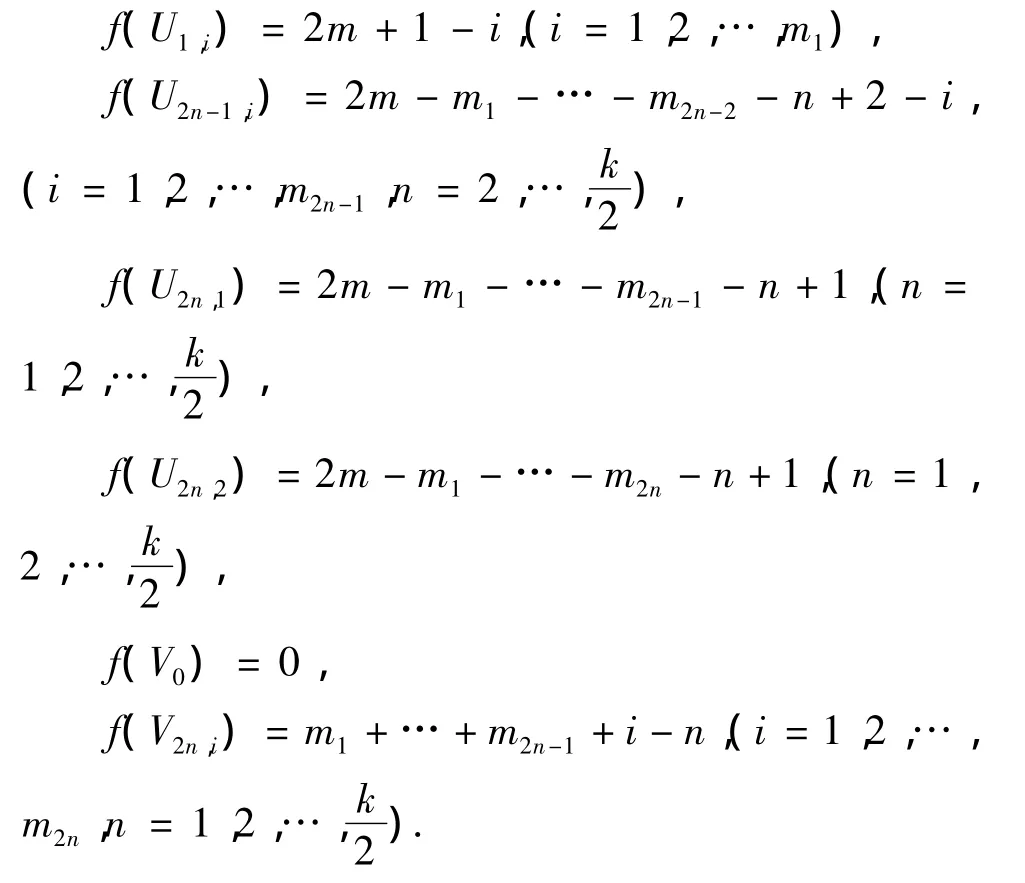
易证得f(v)是图T5的优美标号。

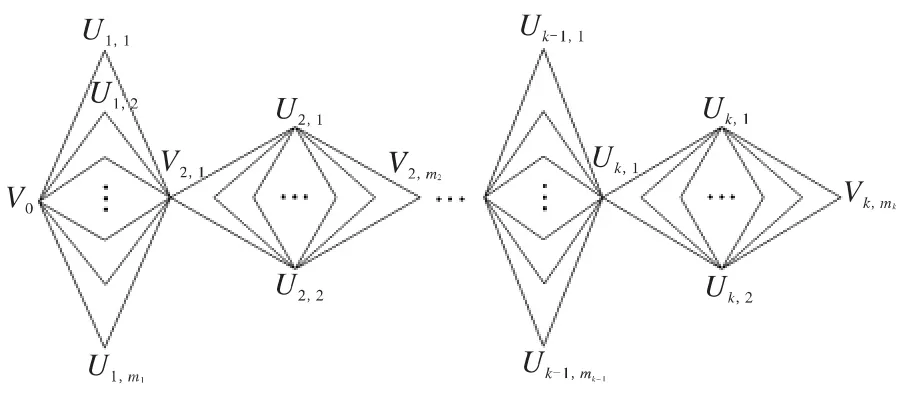
图7 链图T5Fig.7 Chain graph T5

证明了这几类图是优美图，可以猜想将这几类图分别首尾相接而得到的图的优美性。

[1]BONDY J A，MURTY U S R.Graph Theory with Applications[M].New York:Macmillan London and Elsevier，1976.

[2]马杰克.优美图[M].北京:北京大学出版社，1991.

[3]吴丽鸿，王世英.几类图的优美性研究[J].太原师范学院学报:自然科学版，2011，10(3):50-53.

[4]杨显文，于敬莲.关于图 C4∪Fm，4的优美性[J].吉林广播电视大学学报，2002，58(2):54-56.

[7]王天成.一类链图的优美性研究[J].电脑知识与技术，2010，6(19):80-82.

[8]曾一平.等长辐射树Tnm的优美性[J].太原重型机械学院学报，1988，9(1):9-16.

[9]王卫兵，杨徐昕.一类偶阶图的边优美性[J].数学理论与应用，2010，30(2):81-84.

[10]吴跃生，徐保根.关于图的优美性[J].安徽大学学报，2011，35(5):14-17.

[11]李武装，苗宗文，严谦泰.几类有趣图的奇优美性和奇强协调性[J].数学的实践与认识，2011，41(4):234-239.