一种新型板弯单元及其在几何非线性下的应用

黄志强，周 云

(1.太原科技大学应用科学学院数学系，太原 030024;2.西北工业大学理学院，西安 710129;3.西安应用光学研究所，西安 710065)

无人机因其具有成本低、机动性好、能实现“零伤亡”等诸多优良特性而被广泛使用，世界各航空强国均投入大量人力、财力以加速先进无人机系统的研制。从机体平台方面来看，结构轻质化、低可探测性、高机动性、长航时、远航程等特性成为无人机研制的主要技术要求和未来发展方向[1-2]。从结构轻质化角度考虑，由于先进复合材料具有比强度高、比刚度高、抗疲劳能力强等优良性质，故世界上先进的无人机均大量使用复合材料。在大展弦比机翼结构设计时，由于机翼展向尺寸大，故翼根将承受较大弯矩，同时也要求设计人员仔细考虑机翼蒙皮由于弯曲引起的变形和应力。对金属蒙皮而言，应用经典的板壳理论(如Kirchhoff薄板理论)可较为精确地分析其弯曲变形及应力;而对复合材料蒙皮而言，使用经典的弯曲变形理论对其进行分析将导致较大误差，故有必要使用更加精细、恰当的弯曲模型来描述复合材料板壳结构的变形。

本文将介绍一种高阶剪切变形理论及与之对应的四边形有限元，并将该单元用于复合材料层合板的应力分析、变形模拟和结构的几何非线性分析。数值算例表明这种新型单元保证非线性有限元算法的收敛性，能够比较精确计算复合材料板受弯时产生的挠度和应力。

1 Reddy高阶剪切变形理论

较为熟知的板弯曲理论有Kirchhoff薄板理论及一阶剪切变形理论。前者很好地满足力边界条件，但对中厚板而言，横向剪切变形的影响不应忽略;而对于复合材料层合板，当面内弹性模量之比较大(如E11/E22＞25)时，即使其宽厚比满足薄板条件，横向剪切变形的影响也不容忽略。为将横向剪切变形的影响考虑进来，Reissner和Mindlin等人提出了一阶剪切变形理论。但该理论不能精确满足力边界条件，需要引入剪切因子作为修正。对于复合材料层合板，剪切因子和每一层的材料参数、铺层方式、几何形状、边界条件以及其它因素有关，确定起来相当麻烦[3]。

为了不引进剪切因子并保证板上、下表面的力边界条件得到满足，种种高阶剪切变形理论被提出，其中Reddy提出的高阶剪切变形理论非常有代表性[4](以下称“Reddy高阶剪切变形理论”)。该理论假设位移函数为如下形式:

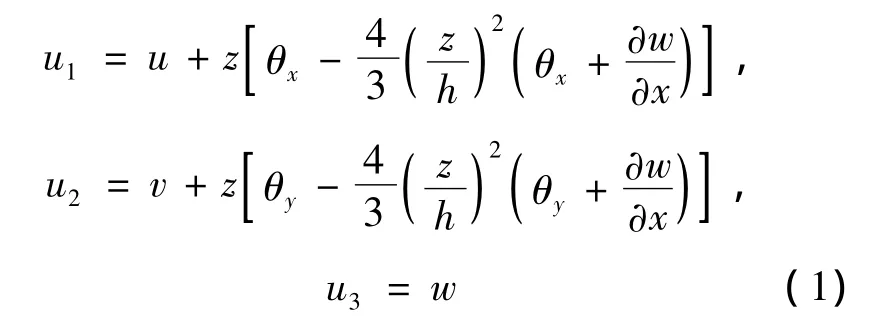
其中 ui(i=1，2，3)分别为某一点处 x、y、z方向的总位移;u、v代表参考面上x、y方向位移，一般由纵向载荷引起;θx和θy为原来垂直中面的纤维在弯后形成的曲线在中面处的转角。不难验证由式(1)所示的位移模式导出的横向剪应变在板上、下表面为零，即:

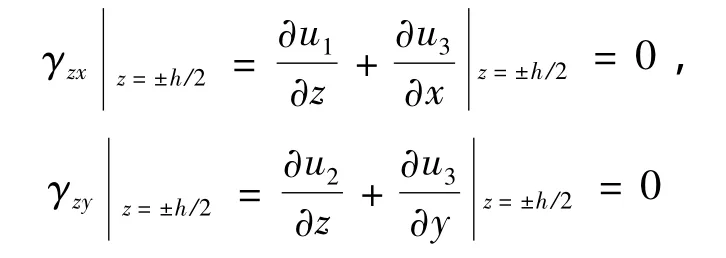
结合复合材料层合板的本构方程可知在板上、下表面横向剪应力也为零，这就达到了无需引入剪切因子就能保证板上、下表面力边界条件精确满足的目的。

3 用于几何非线性计算的HSQ8P单元

由于式(1)所示的位移模式含有挠度的一阶偏导数，这要求在协调的位移型有限元设计时挠度是C1连续的，即挠度本身及其偏导数在计算区域内连续:

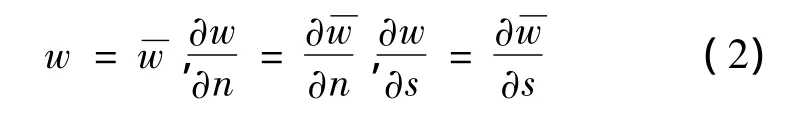
对四边形单元而言，构造C1连续的挠度插值非常困难。于是比式(2)更弱的连续性条件被用来构造挠度，其中一种思路为加权积分意义下的挠度协调。

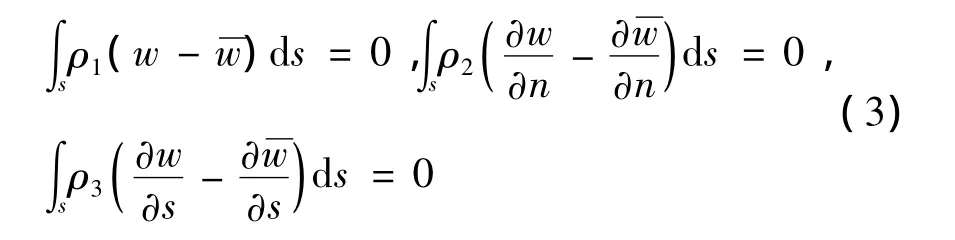
式(3)中 ρi(i=1，2，3)为权函数，可通过对应变能泛函进行变分来确定。从式(3)出发，文献[5]针对四边形网格提出了一种新型挠度插值。以这种挠度插值为基础，文献[6]构造了一种新单元HSQ8P.该单元很好地解决了Reddy高阶剪切变形理论位移型有限元设计时遇到的挠度协调性问题。数值算例显示，在小变形条件下，当网格加密时计算结果收敛于精确解，在四边形网格下HSQ8P元有较高的计算精度。

现考虑将HSQ8P元用于几何非线性条件下的变形、应力分析。对板弯曲问题而言，几何非线性效应主要来自结构较大的刚体平动和刚体转动，而应变往往较小。这种情况下为便于有限元计算，可采用 Green应变和第二类 Piola-Kirchhoff应力(PK2)来描述应变和应力，它们之间的本构关系和小位移条件下本构关系完全一致，相应的计算格式为完全 Lagrange格式(T.L.格式)。类似于文献[7]针对实体单元的分析，现推导HSQ8P元用于几何非线性计算的T.L.格式有限元方程。

对应于T.L.格式的虚功原理为:外力对虚增量位移做的功等于虚应变能增量。假设对第k载荷步的计算已经完成，则第k+1步的应变为:

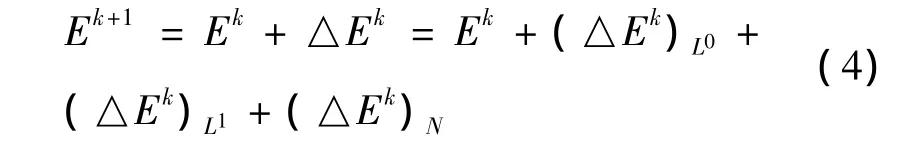
其中Ek为第k步的应变，可由第k步位移表出;虚应变增量可记为:

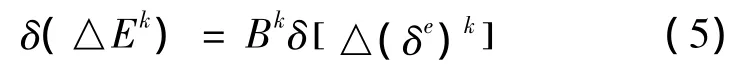
结合式(1)不难给出Bk的显式表达。和应变一样，应力也可以写成增量形式:Sk+1=Sk+△Sk.故在单元上虚功方程为:

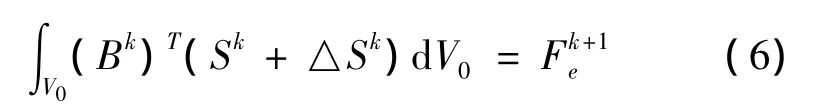
应力、应变之间满足关系:

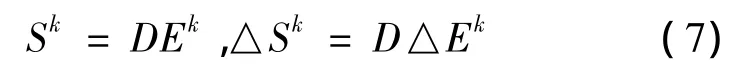
其中D矩阵和几何线性情况下所使用的本构关系矩阵一致。将式(6)按单元组装即可得到有限元方程。

值得指出的是，由于有限元方程中的系数矩阵涉及到应力的计算，故位移解的结果也间接反应出应力的计算精度。

3 数值算例

算例1 复合材料层合板应力计算[8]

正方形层合板几何尺寸、网格剖分如图1所示:h1=h3=h/4;三层的铺层角为分别为0°、90°、0°;材料常数:E11/E22=25，G12=G13=0.5E22，G23=0.2E22，ν12=0.25;边界条件为四边简支;载荷为双正弦分布q=q0sin(πx/a)sin(πy/a).某些关键点处的应力和挠度数值解与精确解之比见表1.从表1不难看出，基于Reddy高阶剪切变形理论的单元HSQ8P能精确地求解层合板的挠度和应力。

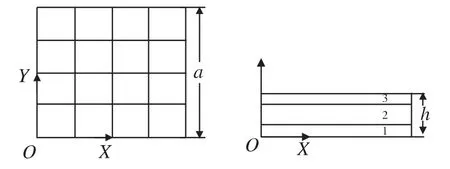
图1 网格剖分及层合板形状Fig.1 Mesh and shape of the laminated plate

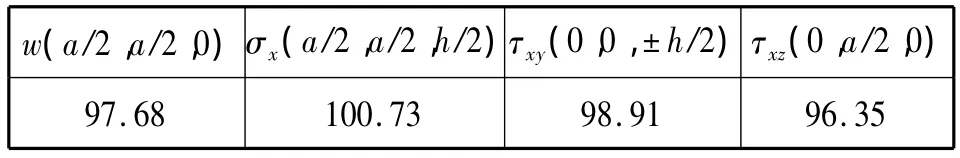
表1 应力和挠度数值解与精确解之比/%Tab.1 Numerical solutions of stress and deflection with the exact solution ratio/%

算例2 各向同性方板的非线性弯曲

计算正方形板在纵向拉伸载荷、横向弯曲载荷耦合作用下的非线性变形。板边长为1，厚度0.2，剖分成16个单元;E=1000，ν=0.3;一端固支，另一端的三个节点施加拉伸-弯曲耦合载荷:f拉=f弯=0.3(如图2 所示)。

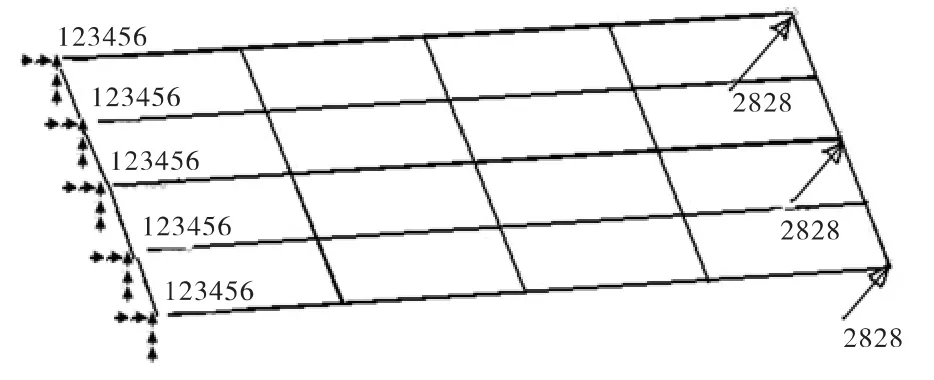
图2 正方形板的网格剖分、边界条件、载荷示意图Fig.2 Square board，mesh，boundary conditions and load diagram

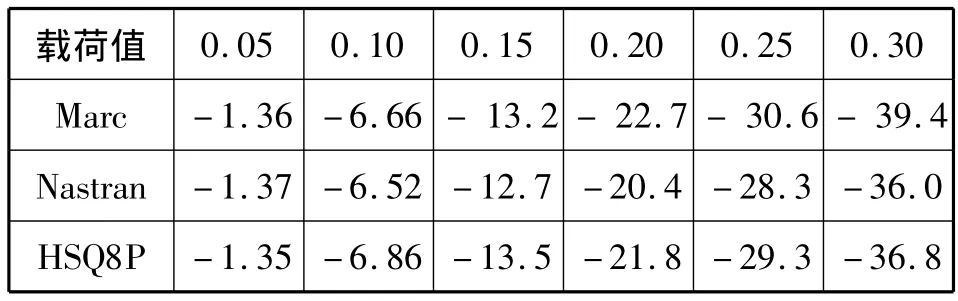
表2 拉-弯载荷下方板自由端中点轴向位移(×10－3)Tab.2 Pull-bending loads below the plate free end of the mid-point axial displacement(×10－3)

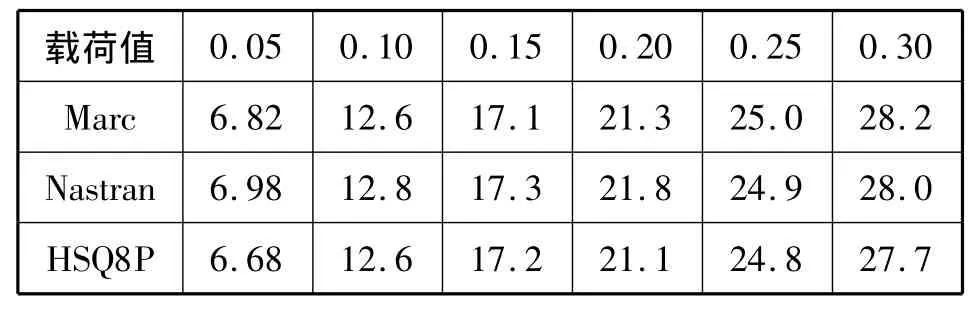
表3 拉-弯载荷下方板自由端中点横向位移(×10－2)Tab.3 Pull-under the bending load plate free end of the midpoint of the horizontal displacement(×10－2)

表2-表3给出了HSQ8P元以及商用FEA软件Nastran进行非线性计算的结果。数据显示HSQ8P有很高的计算精度。

4 结论

将HSQ8P单元的应用范围从小变形条件下位移求解扩展到应力计算、大变形分析，数值算例显示:HSQ8P单元具有较高的位移、应力数值精度，当板结构发生大变形时也能保证结果的收敛性和计算精度。

[1]尹晶.无人机及其复合材料结构优化设计[D].西安:西北工业大学，2009.

[2]马永忠，崔小朝，陶海瑞，等.复合材料锚杆托板的有限元分析与实验研究[J].太原科技大学学报，2007，28(4):327-330.

[3]沈惠申.板壳后屈曲行为[M].上海:上海科学技术出版社，2002.

[4]REDDY J N.A refined nonlinear theory of plates with transverse shear deformation[J].International Journal of Solids and Structures，1984，20:881-896.

[5]周云，孙秦.一种四边形广义协调薄板弯曲单元[J].计算机仿真，2010，27(3):322-325.

[6]周云，孙秦.一种基于高阶剪切变形板模型的有限元算法[J].航空工程进展.2010，1(1):71-75.

[7]凌道盛，徐兴.非线性有限元及程序[M].杭州:浙江大学出版社，2004.

[8]PAGANO N J，HATFIELD S J.Elastic behavior of multilayered bidirectional composites[J].AIAA Journal，1972，10:931-933.