基于改进期望最大化算法的分布式视频编码

李志宏，王海芳

(太原科技大学数字媒体与通信研究所，太原 030024)

随着3G通信技术的飞速发展，低能耗视频摄取设备大量涌现，如移动摄像机、无线传感器网等。由于这些设备的电池能量和内存非常有限，它们要求复杂度低的编码算法，而其解码端由于连接强计算能力的中心计算机(比如移动基站等)，可以容忍复杂度较高的解码算法。这种要求和传统视频编码的“高复杂度编码低复杂度解码”特点形成对比(如H.264，由于其编码端使用了复杂的运动估计算法，其编码算法大致是解码算法的5-10倍)，对传统算法提出了挑战。

分布式视频编码(Distributed Video Coding，DVC)[1]是适应低复杂度编码而出现的一种新型视频编码方法，其框架如图1所示。视频帧分为关键帧(Key frame)和Wyner-Ziv帧(WZ frame)，对关键帧采用传统的帧内编解码方法，对WZ帧采用一种“独立编码联合解码”的方式，即编码端对各个帧不利用时域相关性进行独立编码(对WZ帧仅利用一个量化器和信道编码，编码端仅传输信道编码产生的伴随式s)，而解码端利用相邻帧的时间相关性进行解码(首先利用已解码的相邻帧产生边信息，然后用边信息进行信道解码和量化重构)，从而将运动估计等计算量较大的去时域相关算法从编码端转移到解码端，实现了复杂度较低的编码算法(虽然其解码端造成了较高的计算复杂度)。DVC的这些特点使其非常适用于上述的低能耗视频摄取设备。

DVC中，边信息(Side information，SI)是一个很重要的因素，它是由相邻帧根据时域相关性采用内插(Interpolation)或者外插(Extrapolation)产生的信息。一般而言，边信息越精确，则整个DVC系统的性能越好。为了提高边信息的性能，现有DVC方案利用解码端恢复的相邻帧进行运动估计内插以产生边信息[1-2]，然而，因为恢复帧不准确引起了不准确的运动估计，最终造成边信息性能的下降。为进一步提高边信息性能，Aaron提出一种hash边信息算法[3]，编码器将当前WZ帧的某些特征(如小波高频系数)表示为hash并传到解码器，解码端利用hash辅助运动估计，从而提高运动估计可靠性，并最终得到高性能的边信息。然而，由于编码端需要传送hash信息，会增加系统的码率，从而影响整体系统性能。在上述两种边信息基础之上，D.Varodayan等提出一种无监督学习运动矢量[4-6]的边信息生成方法，利用Wyner-Ziv码流来学习前向运动矢量，称之为期望最大化算法(Expectation Maximization，EM)。实验结果表明，EM是目前性能最好的边信息生成方法，但同时也是计算复杂度最高的方法。对此，为进一步提高EM算法的实用性，需要在保持其性能的前提下，减低其算法的复杂度。在这种动机下，通过深入研究EM算法的原理，提出了两种EM的改进算法，在保持性能的前提下，降低了算法的复杂度。

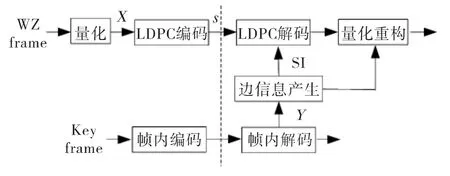
图1 分布式视频编码框架Fig.1 DVC framework

1 期望最大化算法

期望最大化——EM算法分为两个基本步骤:M-step和E-step，如图2所示。

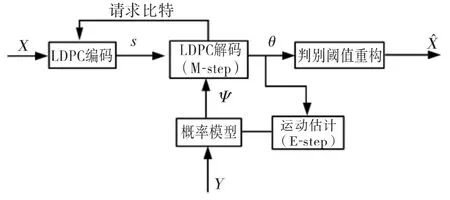
图2 基于无监督运动矢量学习的EM算法Fig.2 EM algorithm with unsupervised motion vector learning

考虑视频中两个连续帧X和Y，其中X是量化版本，Y是解码端的重构版本。设X与Y之间图像块的前向运动矢量场用M表示。EM算法的基本思想是:编码端对X帧进行低密度奇偶校验(Low Density Parity Check，LDPC)编码并逐步发送伴随式比特s，解码端通过M-step算法从LDPC解码流中计算X的软估计θ值，通过E-step将θ与Y值进行比较得到运动矢量场的后验概率值。反复迭代M-step和E-step，可以使软估计θ值和运动矢量场M得到不断更新，边信息ψ也将随M更新而更新，最终找到精确的运动矢量场和精确的边信息。这里，类似于目前所有的DVC方案，LDPC利用接收到的伴随式s和边信息进行迭代解码，如果迭代次数超过预定的次数仍不能解码成功，则通过反馈信道要求发送额外的伴随式比特并重新进行上述的迭代解码。当硬估计产生的伴随式比特等于s时，解码成功。

在EM算法中有两点需要引起注意，其一，运动矢量M表示相邻两帧图像块之间的运动情况，其值反映了当前块向某个方向运动的概率大小，会随着LDPC迭代解码而更新，因此，在LDPC迭代解码之前，需要预先设定一个运动矢量场M以引导每次迭代中M-step和E-step的更新，从而一定程度上决定边信息的性能。其二，E-step利用每次迭代产生的软估计θ值在参考帧中进行搜索并更新运动矢量场M，每次搜索都采用基于块的正方形区域全搜索法，因此造成很大的计算量。本文正是针对这两方面的问题展开研究，实现了EM的两种改进算法。

2 基于菱形搜索改进的EM算法

2.1 算法设计

由以上介绍可以看出，EM算法在整个压缩过程中使用了最耗费计算资源的块匹配运动搜索来更新运动场。EM需要反复进行E-step和M-step步的迭代，反复进行运动矢量场的更新，因此将花费大量时间。在块匹配运动搜索中，搜索模式设计应符合视频的运动矢量概率分布特征。因此，可利用视频的运动分布特征对EM算法进行改进。

文献[7]的分析和实验结果表明，在多种常用的块匹配算法中，当折中考虑搜索性能和速度时，菱形搜索(DS)在是最优的。然而，由于单纯DS算法难以与EM算法结合，因此将采用一种固定的菱形搜索模板，如图3所示。这个模板中，固定地使用正方形的菱形中心，由于菱形中心反映了相邻视频帧之间图像块的运动规律(即图像块向下一帧中相同位置(即中心位置)运动的概率大，向远离中心位置运动的概率小)，因此这种算法可以很快找到全局最小值，并且搜索性能接近正方形模板全搜索。

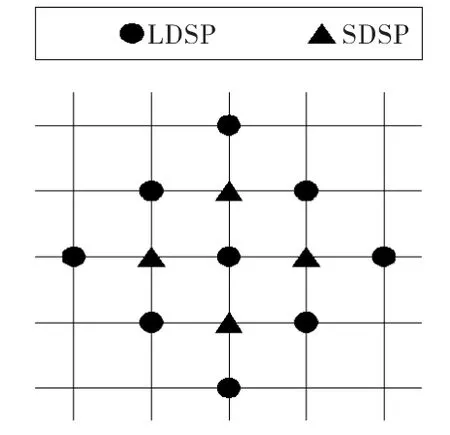
图3 菱形模板搜索范围Fig.3 Searching region of diamond model

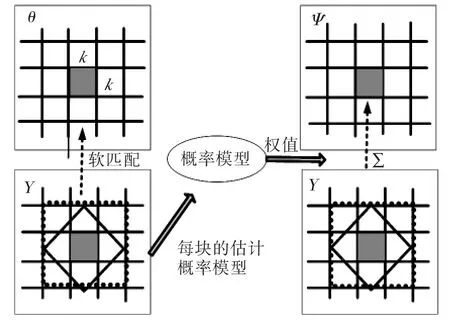
图4 改进的EM算法Fig.4 Improved EM algorithm

如图4所示，左下图中，虚线的正方形区域表示文献[6]中EM的全搜索区域，实线的菱形区域表示根据图3的菱形模板所确定的搜索区域。基于菱形搜索的EM算法具体步骤为:对X中的每个k×k块，根据其LDPC解码后的软估计θ值在中Y的菱形区域进行搜索(替代正方形区域的全搜索)，计算运动矢量的概率模型，将此概率模型值与Y中保存的概率模型进行加权和运算求得ψ，并用ψ更新中Y的概率模型。重复下列过程:LDPC迭代解码→基于软估计θ值进行菱形模板运动搜索→估计运动矢量概率模型→求得ψ并更新Y→直到某位置的概率达到最大值1，即为最佳的运动矢量，从而得到最好的边信息Y.

由图3可以看出，菱形模板搜索次数只有正方行模板的13/25，因此，大大降低了搜索时间;同时，由于菱形窗模板考虑到图像块的运动特点(远离中心点的运动概率小，靠近中心点的运动概率大)，因此，基于菱形模板的运动搜索的性能与正方形相差不大。这里，所采用的菱形搜索初始概率根据式(6)来确定:

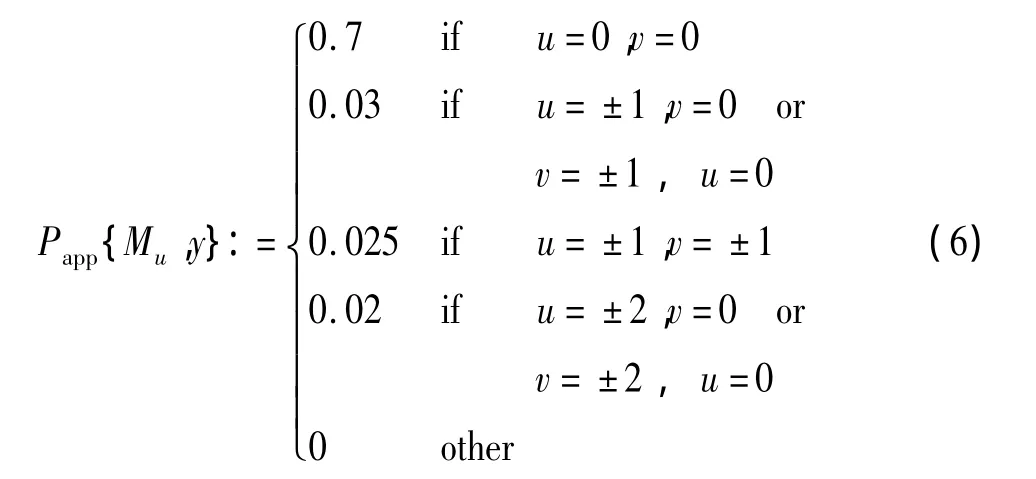
其中，u和v分别表示运动矢量的水平和垂直分量，Mu，v表示运动矢量(u，v)的概率，搜索范围为:u∈[－2，2]，v∈[－2，2]。

2.2 实验结果与分析

根据文献[6]提供的程序代码，实现了变换域分布式视频编码，框架如图5所示。编码端对WZ帧进行分块DCT(即，块离散余弦变换)，然后对变换所得系数进行量化。上述的改进EM算法用于框架中的运动估计部分。利用两个标准的视频序列:Foreman和Hall@30 Hz进行测试，运动矢量估计在水平和垂直方向5个像素的范围内，即u∈[－2，2]，v∈[－2，2]。最大迭代次数为50次。

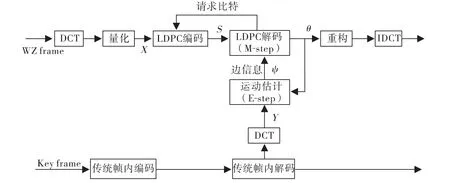
图5 基于EM的变换域分布式视频编码Fig.5 DVC based on EM Transform domain

实验结果如图6和图7所示，比较了三种算法的率失真(rate-PSNR)性能，包括理想运动矢量、文献[6]中的正方形模板EM和本文提出的菱形模板EM，相对应的搜索时间如表1所示。结果表明，菱形模板EM算法比文献[6]中的正方形模板EM节省了30%的搜索学习时间，但其性能并没有明显下降。

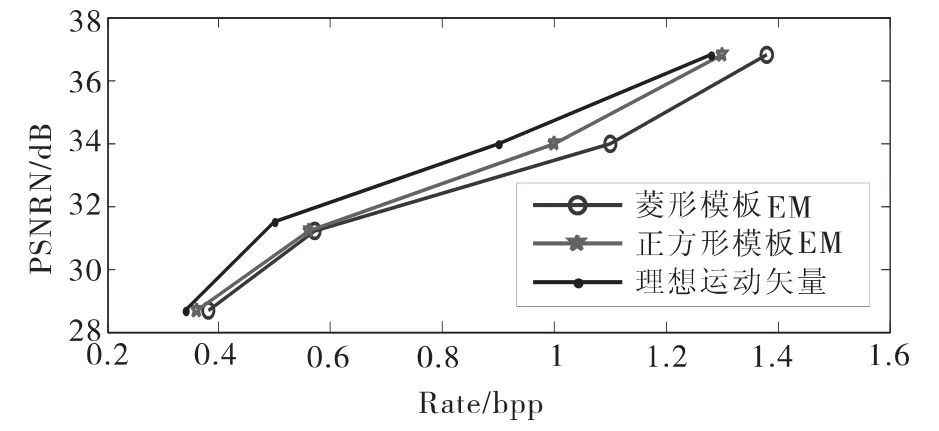
图6 GOP=8的Foreman率失真性能Fig.6 Rate-distortion performance of Foreman sequence when GOP=8

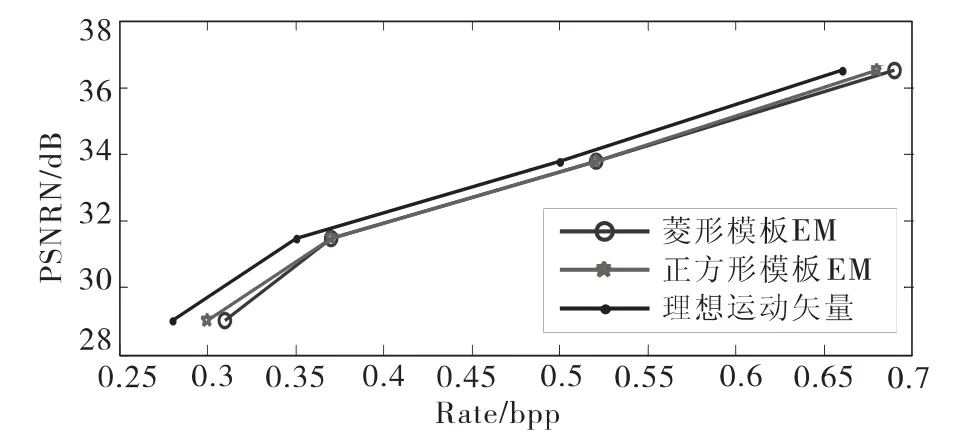
图7 GOP=8的Hall率失真性能Fig.7 Rate-distortion performance of Hall sequence when GOP=8

表1 两种算法的学习时间比较Tab.1 Comparison of learning time of two methods

3 基于自适应初始概率改进的EM算法

3.1 算法设计

由上述分析可知，在EM算法运动矢量概率模型M的学习过程中，初始概率模型起着关键的作用。文献[6]中，EM算法采用了固定的概率模型，忽略了视频帧间运动矢量的多变性，对此，提出了根据视频的实际运动情况采用一种自适应的概率模型来进行改进，即在编码端首先判断帧的运动情况，然后根据运动情况预定初始的概率模型。具体而言，采用相邻两帧差的绝对值SAD来判断两帧之间的运动情况，如果SAD值大于某个事先设定的阈值，则认为这两帧之间的运动幅度较大，将采用中心概率值小的初始概率模型;如果SAD值小于某个事先设定的阈值，则认为这两帧之间的运动幅度小，将采用中心概率值大的初始概率模型;其余块的概率再根据中心概率而定。根据实验确定阈值Th，每块的初始化运动矢量概率Mu，v如下，

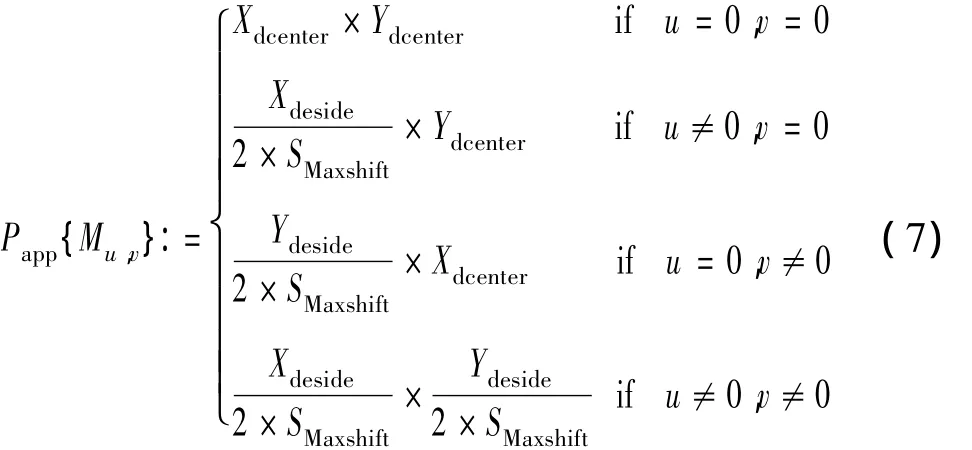
当两帧之间的SAD值大于设定的阈值Th时，给中心点概率Xdcenter和Ydcenter赋较小的概率值，相反，当SAD小于阈值Th时，给Xdcenter和Ydcenter赋一个较大的概率值，其他方向的概率会随着中心概率值的变化而变化。

3.2 实验结果与分析

采用相同的实验环境。经过大量实验，对于Foreman视频序列，取阈值Th=200000.如果阈值SAD ＞ Th，则 Xdcenter=Ydcenter=0.7;否则 Xdcenter=Ydcenter=0.8.

对于Hall视频，因为序列整体运动较缓慢，将EM算法的中心概率定为Xdcenter=Ydcenter=0.9，取阈值Th=500000，如果SAD ＞ Th，Xdcenter=Ydcenter=0.8;否则，Xdcenter=Ydcenter=0.9.

表2是两个概率模型在相同率失真性能下的学习时间比较，很明显，概率自适应EM算法在保持同样的率失真性能下，节约了16%的学习时间。

表2 两种算法的学习时间比较Tab.2 Comparison of learning time of two methods

4 结论

EM算法是一种相对优异的DVC产生边信息的方法，它是基于块的全搜索对产生的运动矢量进行学习。由于全搜索非常耗时使得EM的学习时间很长，因此，本文提出了采用菱形搜索优化的改进EM算法，减少了搜索点，并能很快找到全局最小值。同时，由于在运动矢量概率模型的学习过程中，初始概率模型起到很关键的作用，对此，本文提出采用基于初始概率模型自适应的EM算法。实验结果表明，基于菱形搜索的EM算法和初始概率自适应的EM算法在保持同样的率失真性能下，分别节约了30%和16%的学习时间。

[1]GRIOD B，AARON A，RANE S.Distirbuted Video Coding[J].Proceedings of the IEEE，2005，93(1):71-83.

[2]WYNER A，ZIV J.The Rate-distortion Function for Source Coding with Side Information at the Decoder[J].IEEE Transaction on Information Theory，1976，22(1):1-10.

[3]AARON A，RANE S，GRIOD B.Wyner-Ziv Video Coding with Hash-based Motion Compensation at the Receiver[C]//IEEE Int Conf Image Processing，Singapore，2004:3097-3100.

[4]VARODAYAN D，MAVLANKAR A，FLIERL M，GIROD B.Distributed grayscale stereo image coding with unsupervised learning of disparity[C]//IEEE Data Compression Conf，Snowbird，UT，2007:143-152.

[5]VARODAYAN D，LIN Y C，MAVLANKAR A，FLIERL M，GIROD B.Wyner-Ziv coding of stereo images with unsupervised learning of disparity[C]//Picture Coding Symp，Lisbon，Portugal，2007.

[6]VARODAYAN D，CHEN D，FLIERL M，GIROD B.Wyner-Ziv coding of video with unsupervised motion vector learning[J].Signal Processing:Image Communication，2008，23(5):369-378.

[7]Aroh Barjatya.Block matching algorithm for motion estimation[J].IEEE Transactions Evolution Computation，2004，8(3):225-239.