决策树ID3算法的一种改进

赵 静

沈阳市服装艺术学校，辽宁沈阳 110032

1 ID3算法简介

ID3算法由Quinlan于1979年提出。其基本思想是：在对训练集进行分类时，以信息熵为度量，用于决策树节点的属性选择，每次优先选取信息量最多的属性对数据进行划分，以构造一颗熵值下降最快的决策树，每个叶子节点对应的实例集中的实例属于同一类。

2 ID3算法的优点和不足

优点：运用信息论知识选择属性，理论清晰；容易生成IF-THEN语句；对于离散型样本数据处理功能强；ID3自顶向下搜索，节省系统资源，计算时间与样本大小。

不足：ID3算法在选择分类属性时往往选择了取值较多的属性；ID3算法只能处理离散型数据，若分析必须先进行离散化；用ID3算法创建决策树时必须知道所有内部节点。

3 ID3算法的改进

定理1：若函数f(x)在[a，b]上连续，在（a，b）内有一阶、二阶导数，并且在（a，b）上，若f'(x)＜0，则f(x)在[a，b]上是凸函数；

3.1 算法改进的实现

pi表示数据属于类Ci的概率，在（0，1）上任取p1，p2有p1+p2=1，p1-p2=△p→0，因为log2p函数在（0，1]上连续，由定理1可知log2p函数在其连续区间上是凸函数。

由凸函数性质计算得：

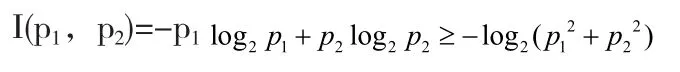
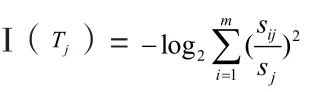
3.2 改进算法的应用

表一为某公司调查的顾客数据统计表.通过数据挖掘旨在回答“谁在买电脑”这一问题。

表1 顾客调查表

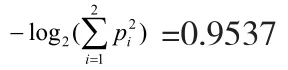
第2步：计算条件属性的熵

1）年龄分三组:老、中、青。 青年384人，正例128人，反例256人；中年256人，正例256人，反例0人；老年252人，正例125，反例127人。

老年 ： I(125，127)=0.9157 所以 ，E（年龄）=0.6877 ； G（年龄）=0.9537-0.6877 =0.2660 ；

2）E（收入）=0.9361 G（收入信息增益）=0.9537-0.9361=0.0176；

3）E（学生）=0.7811 G（年龄信息增益）=0.9537-0.7811=0.1726；

4）E（信誉）=0.9048 G(信誉信息增益）=0.9537-0.9048=0.0453。

第3步：计算选择节点。由上可知“年龄”具有最高的信息增益，选择“年龄”为测试属性 。

第4步：递归建树算法，分别对各个子集分析，计算选择分支的测试属性。

1）年龄=“青年”的子集有：选择学生为测试属性对子集进行再划分；

2）对于年龄=“中年”，数据都属于同一类，自然形成树叶；

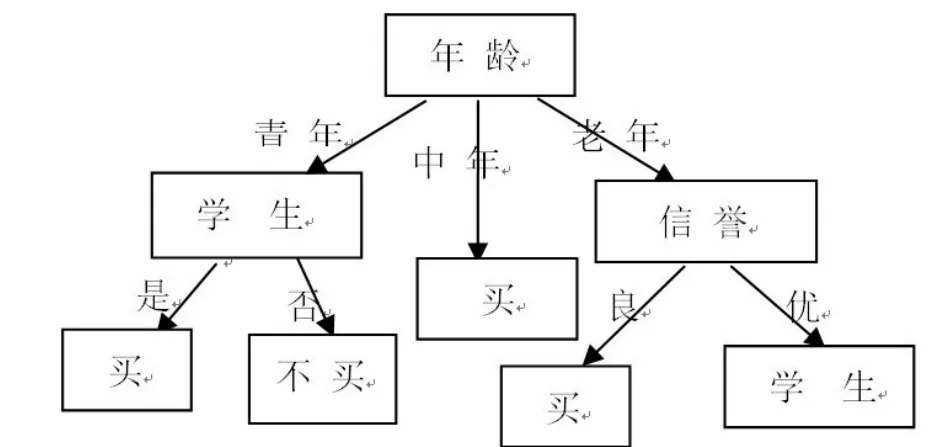
3）对于年龄=“老年”的子集有：选择信誉为测试属性。由此生成决策树如下图所示：