引入权重因子的Fisher判别法的研究

赵丽娜

(东北林业大学)

0 引言

费歇(Fisher)判别法是二十世纪三十年代由Fisher提出的.它的基本思想是投影，特点是将高维数据点投影到低维空间上，使数据点变得比较密集进而可以克服由于维数高引起的“维数祸根”.根据类间距离最大、类内距离最小的原则确定判别函数，在根据建立的判别函数判定待定样品的类别.

由于Fisher判别分析方法不需要对样本数据进行检验，而且有一定的正确率，因此，在实际中它得到了广泛的应用，如:鲁立强等利用Fisher判别方法对苹果的品质鉴别进行判别取得了良好的成果;钟绍军等利用Fisher判别法，对未知乳房肿瘤性质的病例进行了成功的诊断，使得费歇判别法在医学领域发挥巨大的作用;葛和平利用Fisher判别分析对我国上市公司财务困境进行了分析研究，取得重要成果.近年来，Fisher在人脸识别技术、公司信用评价以及肉质寒热性等更多的领域得到发展研究.

1 预备知识

现考虑在Rp中将m组的p维数据向量投影到某个具有最佳方向的α上，也就是说，投影到α上的点能最大限度的体现出各组之间的差异.令来自总体中的p维观测值为xpq，q=1，2，…，np，p=1，2，…，m，把他们都投影到p维常数向量 α上，得到的投射点分别对应线性组合ypq=α'xpq，q=1，2，…，np，p=1，2，…，m.用 yp表示一组中ypq的均值，y表示所有组ypq的总均值.即yp=其中假定各组的协方差矩阵相等，即.则组间平方和= α'Qα，其中'为组间平方和.ypq的组内平方和= αFα其中E=为组内平方和.Q和F分别表示类之间和类内部的差异.根据判别函数找到一组c1，c2，…，cp使得Q最大而F最小，从而使组间差别最大组内离差最小.于是可得模型，要达到最大值，就是求F-1Q的最大特征根.取，其中β为的最大特征根对应的特征向量.

两个总体的判别准则:一般取y0为y(1)与y(2)的加权平均值，即则判别准则为:对于一个新样品X=(x1，…，xp)T代入判别函数中去所得值记为y，若y＞y0，则判定X∈G1;y＜y0，则判定X∈G2.如果y(1)＜y(2)，则建立判别准则为:若y＞y0，则判定X∈G2;若y＜y0，则判定X∈G1.该文只考虑多总体的情况.

多总体的判别准则:假设把总体分成p个类，若|yp-y1|＜|yp-yq|，(p，q=1，2，…，m，q≠1)，则yp属于第1个类.

定理1［1］若A是p阶对称矩阵，B是p阶正定矩阵，μ1≥μ2≥…≥μp是B-1A的p个特征值，则

2 主要结果

把费歇判别法改进主要是在原判别函数建立的情况下改进判别函数，引入权重因子，于是原模型由改为=ρC'QC-(1-ρ)C'FC，化简为Ⅰmax=C'［ρ(Q+F)-F］C，易知这是标准的二次型，由定理1可知模型的解C为ρ(Q+F)-F的最大特征根对应的特征向量.因此ρ取0到1之间的数值代入模型可得到多个不同的解，根据回判率来确定ρ的最佳取值，得到最佳的判别函数.

权重因子:权重因子ρ是衡量个体在总体中的比重的指标，所以ρ越大说明这个个体的比重就越大，常将权重因子取值在(0，1)之间，可以通过调整ρ的取值来调整组间距与组内距在模型中的比重大小.

3 实例分析

例1 从癌症患者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行四项生化指标的化验:血清铜蛋白(X1)、蓝色反应(X2)、尿吲哚乙酸(X3)和中性硫化物(X4)，具体数据见文献［2］中7.7.

用SPSS软件得到的分析结果如下:

对这些数据用原来判别函数模型，可得:

判据为-78.9512，回判率为96.3%.

再用改进的引入权重因子的判别模型，分别取ρ=0，1，0.2，…，0.9，可得:

通过 SPSS 软件得出ρ在［0.1，0.2］区间内回判率最佳，即回判率100%.将原判别模型下的回判率(96.3%)与改进后的模型下的回判率100%比较，不难发现改进后的模型下的回判率有了显著的提高.

例2 对全国30个省市自治区1994年影响各地区经济增长差异的制度变量:X1表示经济增长率，X2表示非国有化水平，X3表示开放度，X4表示市场化程度.数据见文献［3］.

分别取ρ=0.1，0.2，…0.9，通过 SPSS 软件可得:

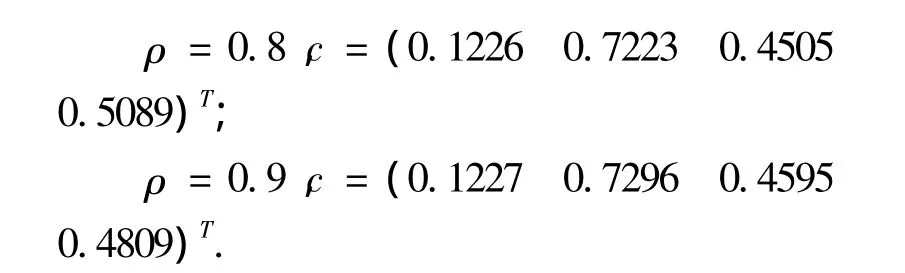
通过软件发现在［0.5，0.9］区间内回判率比较好.由文献［3］我们可知在原费歇判别模型下，此问题的回判率是92.5%，通过改进后的模型计算发现回判率有所提高为96.3%.

4 结论

与Fisher原判别模型相比，引入权重的进而得到改进的费歇尔判别法在作判别时，只需要变换ρ的取值，就可以得到多种结果，进而找到最好的判别模型和最佳的判别效果，这样判别更准确，而且得到的判别模型也更加稳定.虽然ρ多次取值，增加了计算难度，但在计算机技术飞速发展的今天，完全可以解决这个问题.所以，认为引入权重因子的Fisher原判别方法更准确，效果更好.

［1］ 王学民，方开泰.多元统计分析引论［M］.北京:科学出版社，1999.

［2］ 管宇.实用多元统计分析［M］.杭州:浙江大学出版社，2011.10.

［3］ 于秀林，任雪松.多元统计分析［M］.北京:中国统计出版社，1999.

［4］ 游华，郭福星.最优组合因子 Fisher判别法［J］.福州大学学报:自然科学版，2001(3):1-4