一类三阶非线性微分方程的渐近概周期解*
姚慧丽,张琳琳
(哈尔滨理工大学)
0 引言
非线性微分方程在实际问题中有着许多应用,如物理学中的机械振动,电力学理论等等,正因如此,多年来,很多科学工作者研究了此类方程的各种解的存在性,稳定性,收敛性[1-4],文献[5]对于方程(1)的概周期解的存在性问题进行了讨论.该文主要运用Banach不动点定理和渐近概周期函数的有关性质讨论了三阶非线性微分方程
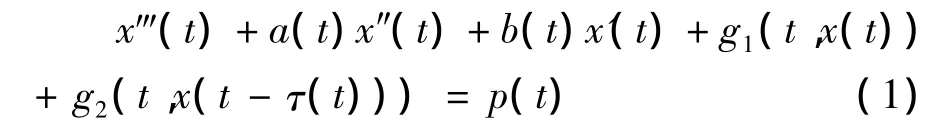
的渐近概周期解的存在性与唯一性.
设k1,k2为常数,令
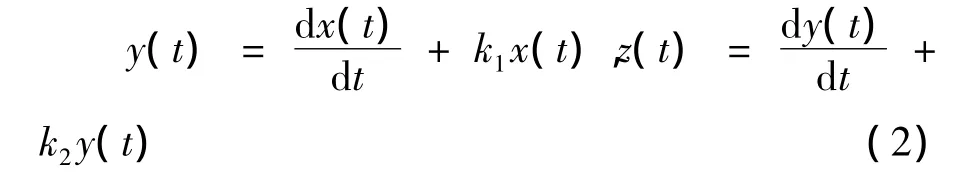
则方程(1)可转化为以下方程
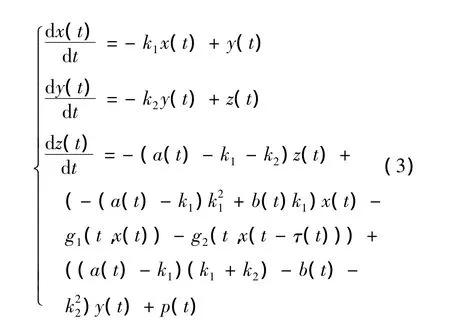
1 预备知识
该文R为实数集,C(R)表示R上的有界连续函数的全体.
定义1.1 称f(t)∈C(R)为概周期函数是指对于任意的ε>0,存在一个实数lε>0,对长度为lε的任意区间都包含一个常数τ,使得|f(t)-f(t+τ)|<ε,用AP(R)来表示此类函数的全体.
定义1.2 称f为渐近概周期的,是指f可以写成

用AAP(R)表示这样函数的全体.其中C0(R)=
引 理 2.1[6]如 果f∈AAP(R),F∈AAP(R),则f(F(·),·)∈AAP(R).
2 主要结果
首先假设以下条件成立:
(H1)a(t)为 R上的概周期函数;b(t),p(t),τ(t),g1和g2均为R上的渐近概周期函数.
(H2)存在常数L1≥0,L2≥0,k1>1,k2>1,k3>0,使得
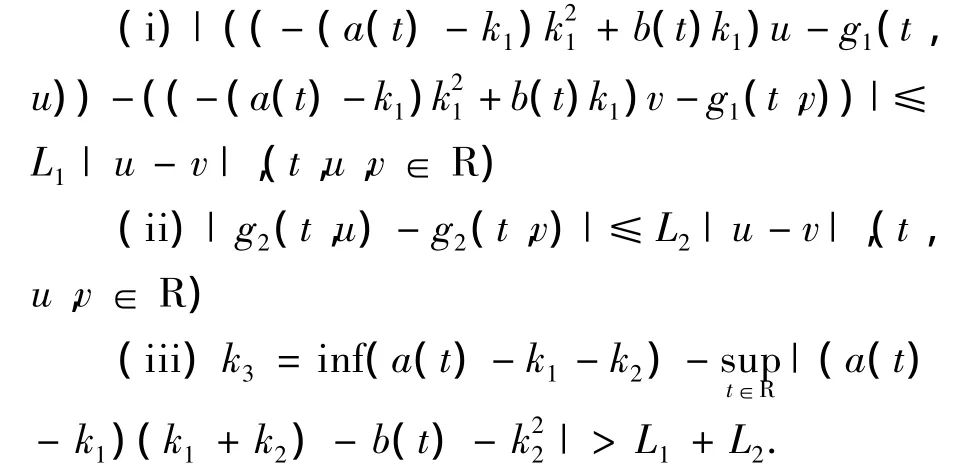
定理2.1 设(H1),(H2)成立,则方程(3)存在唯一一个渐近概周期解.
证明 令X={φ=(φ1(t),φ2(t),φ3(t))},其中φi(i=1,2,3)为R上的渐近概周期函数,则X为 Banach空间,且 ‖φ‖X=
引入辅助方程

这里φ(t)=(φ1(t),φ2(t),φ3(t))∈X,a(t)为概周期函数;b(t),p(t),τ(t),g1和g2均为渐近概周期函数,根据文献[7]知辅助方程(4)有如下形式的解,


下面证明此解Xφ(t)为渐近概周期的:
因为φi(i=1,2,3)为渐近概周期函数,则令φ1(s)=h1(s)+φ1(s),φ2(s)=h2(s)+φ2(s),φ3(s)=h3(s)+φ3(s),其中h1,h2,h3∈AP(R),φ1,φ2,φ3∈C0(R),xφ(t)=

因为φ2(s)∈C0(R),所以对任意的ε>0,存在T1>0,使得当|s|>T1时,有|φ2(s)|<ε.又因为=0(c为常数),所以存在T2>0,当t>T2时,有.取T=max{T1,T2},因为φ2(s)为有界函数,所以当s∈[-T,T]时,存在M>0,使得|φ2(s)|≤M.
(1)t>T时


为渐近概周期的.
因为φi(i=1,2,3),b(t),p(t)为渐近概周期函数,则令φ1(s)=h1(s)+φ1(s),φ2(s)=h2(s)+φ2(s),b(s)=α(s)+β(s),p(s)=γ(s)+η(s),其中h1(s),h2(s),α(s),γ(s)∈AP(R),φ1(s),φ2(s),β(s),η(s)∈C0(R),又因为g1,g2,τ(t)是渐近概周期的,所以由引理1.1知g1(s,φ1(s)),φ2(s-τ(s))是渐近概周期的,g2(s,φ1(s-τ(s)))是渐近概周期的,记Ⅰ1(s)=g1(s,φ1(s))=λ(s)+μ(s),Ⅰ2(s)=g2(s,φ1(s-τ(s)))=ω(s)+ζ(s),其中λ(s),ω(s)∈AP(R),μ(s),ζ(s)∈C0(R),则



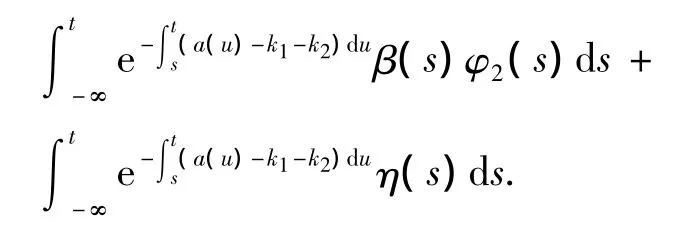
由(H2)-(iii)知L2,所以

因为φ1(s)∈C0(R),所以对任意的ε0,存在T1>0,对任意的|s|>T1,有|φ1(s)|<ε.
取T=max{T1,T2},因为s∈[-T,T]时,φ1(s)为有界函数,所以存在M>0,使得

因为a(s),α(s)∈AP(R),所以-(a(s)-,所以+α(s)k1为有界函数,所以对任意的s∈R,存在
N>0,使得
①t>T时

②t<-T时

综合①②可知


类似可证明Z2(t)中余下的八项所表达的函数都属于C0(R).
则zφ(t)是渐近概周期的.
由(1),(2),(3)可知,辅助方程(4)的解为渐近概周期的.
定义映射Φ:X→X
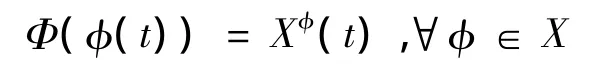
设φ,ψ∈X,根据条件(H2),有,

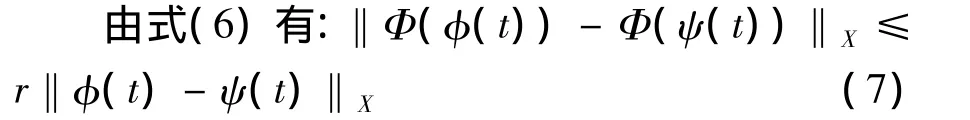
由条件(H2)知r<1,即映射Φ:X→X为压缩映射.根据Banach不动点定理知Φ在X上存在唯一的不动点v,即Φv=v,由式(5)知v是方程(3)的渐近概周期解.
[1] Afuwape A U,Omari P,Zanolin F.Nonlinear Perturbations of differential Operators with nontrivial kernel and applications to third-order periodic boundary problem.Journal of Mathematical Analysis and Applications,1989,143:35-56.
[2] Andres J.Periodic boundary value problem for certain nonlinear differential equation of the third order.Mathematica Slovaca,1985,35:305-309.
[3] Fridedrichs K O.On nonlinear vibrations of the third-order,Studies in Nonlinear Vibrations Theory.Institution Mathematic and Mechine,New York Universtity,1949.
[4] Rauch L L.Oscillations of a third order nonlinear autonomous system in:Contributions to the Theory of Nonlinear Oscillations.Annal of Mathematical Study,1950(20):39-88.
[5] 易学军.几类泛函微分与差分方程的收敛性.湖南大学:博士论文,2009.
[6] Zhang C.Almost Periodic Type Functions and Ergodicity[M].Science Press/Kluwer Academic Publish,2003.1-70.
[7] 丁同仁.常微分方程定性方法的应用.北京:高等教育出版社,2004.155-163.
[8] 易泰山,黄立宏.关于Bernfeld-Haddock猜想的推广形式及其证明.数学学报,2007,50(2):261-270.

