共轭A-调和张量全局加Ar(λ，Ω)-权估计式*

贺 丹，金明浩

(黑龙江工程学院)

0 引言

p-调和方程div(Δu|Δu|p-2)=0是Rn中关于函数的A-调和方程divA(x，Δu)=0的特例，而A-调和方程divA(x，Δu)=0是非齐次A-调和方程divA(x，Δu)=B(x，Δu)的特例，其中对几乎所有的x∈Ω及所有ξ∈Rn满足

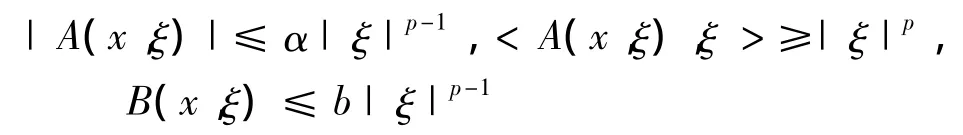
这里A:Rn×Rn→Rn，B:Rn×Rn→R均可测，1＜p＜∞ 且a，b＞0是常数.

近年来，非齐次A-调和方程的理论研究取得了很大进展，该文将给出非齐次A-调和方程

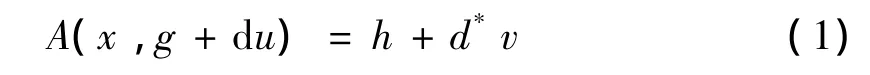
及共轭A-调和方程

解的全局加权范数估计式.

定理1 设u和v是非齐次A-调和方程(1)在Ω上的解，

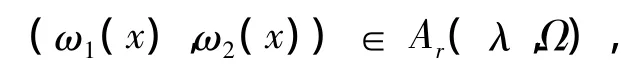
r＞1，那么存在一不依赖于u和v的常数C，使得对所有的球Q，若Q⊂Ω，有

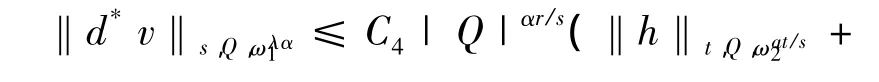
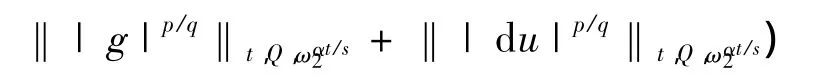
这里α是一正常数，

定理2 设u和v是非齐次A-调和方程(1)在Ω上的解，(ω1(x)，ω2(x))∈Ar(λ，Ω)，r＞1，那么存在不依赖于u和v的常数C，使得对所有的球体Q，若Q⊂Ω，有

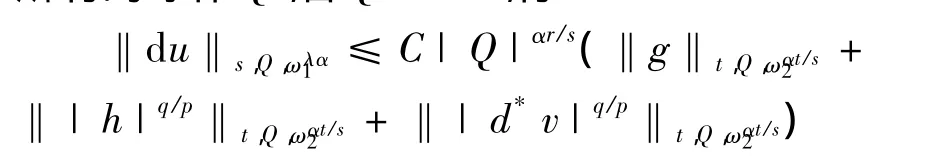
这里 α 是一正常数，αr＜1，s=(1-α)p，t=

引理1 任一Ω均有一Whitney覆盖V={Qi}，使得对所有x∈Rn及N＞1有

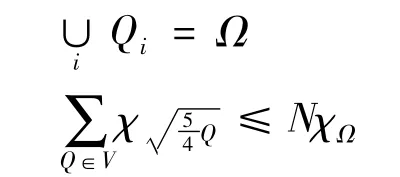
如果Qi∩Qj≠φ，那么存在一立体R(R不一定属于V)，使得Qi∪Qj⊂NR特别地，当Ω是一δ-张量域，那么在V内存在一立体集，使得对某一 ρ= ρ(n，δ)，有Q⊂ ρQi，i=0，1，…，k这里Q为V内的任意立体.

现在来证明下面的全局范数估计定理.

定理3 设u和v是非齐次A-调和方程(1)在有界域 Ω 上的解，(ω1(x)，ω2(x))∈Ar(λ，Ω)，r＞1，那么存在不依赖于u和v的常数C，有

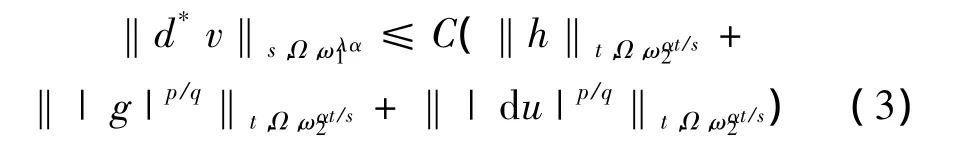
这里 α 是一正常数，αr＜1，s=(1-α)q，t=

证明 应用定理1及引理1，便得

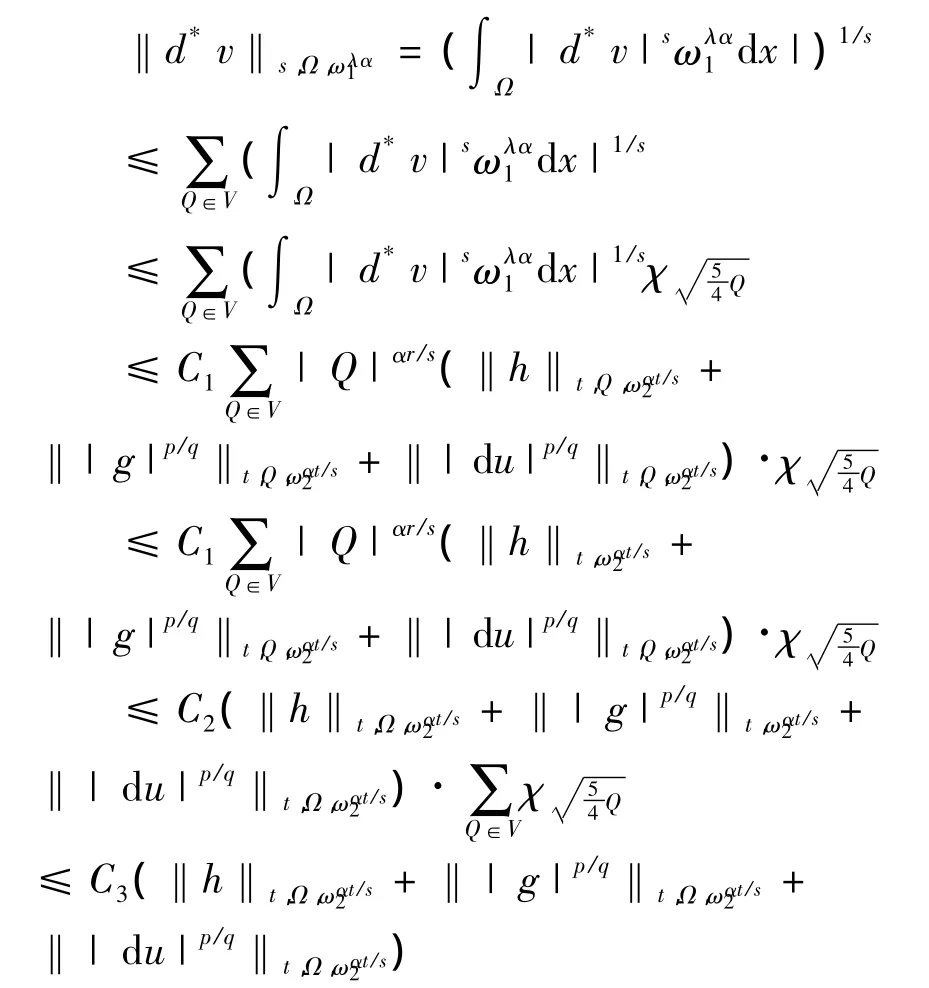
证毕.

在定理3中，令g=0、h=0，于是便得到下面的结论.

推论1 设u和v是共轭A-调和方程(2)在有界域 Ω 上的解，(ω1(x)，ω2(x))∈Ar(λ，Ω)，r＞1，那么存在不依赖于u和v的常数C，αr＜1，有

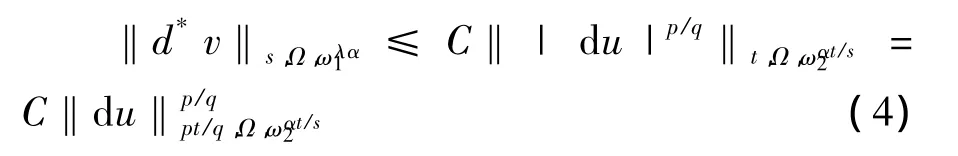
应用定理2及引理1，便可以得出下面的全局的du的Ls-估计.

定理4 设u和v是非齐次A-调和方程(1)在有界域 Ω 上的解，(ω1(x)，ω2(x))∈Ar(λ，Ω)，r＞1，那么存在不依赖于u和v的常数C，有

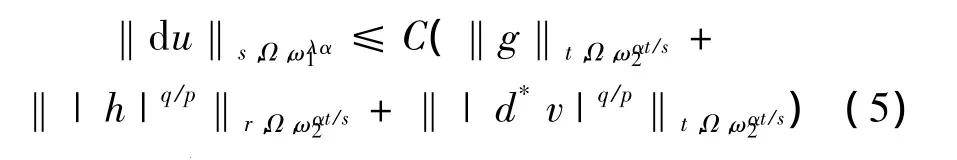
这里α是一正常数，

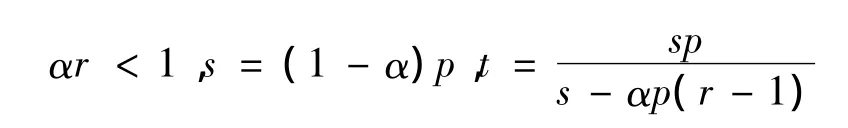
类似地，在定理4中，令g=0、h=0，于是便得到下面的结论.

推论2 设u和v是共轭A-调和方程(2)在有界域 Ω 上的解，(ω1(x)，ω2(x))∈Ar(λ，Ω)，r＞1，那么存在不依赖于u和v的常数C，αr＜1，有

这里 α 是一正常数，αr＜1，s=(1-α)p，t=

［1］ 徐昌贵.一类调和方程边值问题的级数解.漳州师范学院学报:自然科学版，2008，21(1):12-15.

［2］ Nolder C A.Hardy-Littlewood Theorems forA-harmonic Tensors.Illinois Journal of Mathematics，1999，43:613-631.

［3］ Xing Y.Weighted PoincaréA-type Estimates for ConjugateA-harmonic Tensors，J Inequal Appl，2005(1):1-6.

［4］ Wang Y.Two-weighted Poincaré-type Inequalities for Differential Forms inLs(μ )-averaging Domains.Applied Mathmatics Letters，2007，20:1161-1166.

［5］ Nolder C.A.A Quasi-regular Analogue of Theorem of Hardy-Littlewood.Trans Amer Math Soc，1992，331(1):215-226.

［6］ Ding S.Weighted Caccioppoli-type Estimates and Weak Reverse Hölder Inequalities forA-harmonic Tensors.Proc Amer Math Soc，1999，27:2657-2664.

［7］ Zhu M.On the Extremal Functions of Sobolev-Poincaré Inequality.Pacific J Math，2004，214(1):185-199.