不同维度下Laplace 方程解的性质研究

任 磊，段光爽

(信阳师范学院数学与信息科学学院，河南 信阳 464000)

在Newton的万有引力理论中［1］，在固定时间，万有引力加速度向量场(单位质量的力)为-▽u，其中▽u=uxi+uyj+uzk是函数u(x，y，z)的梯度，称为万有引力位势.函数u(x，y，z)服从二阶偏微分方程［2－3］

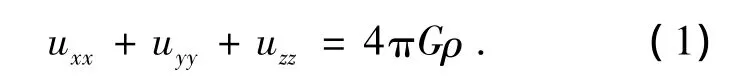
其中:ρ= ρ(x，y，z)为物体在(x，y，z)处的密度，G是万有引力常数，G≈6.668×10-11m3·s－2·kg-1.方程(1)称为 Poisson 方程，当 ρ=0时称为Laplace方程.

1 解的形式和性质

寻求 Laplace方程一个球对称的解 u(x，y，z)，即u(x，y，z)只依赖于到原点的距离

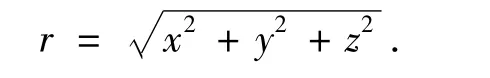
定理1 在n维空间中，Laplace方程有球对称解，其解具有如下形式:

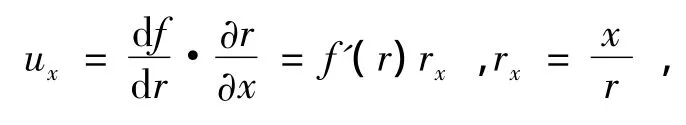
从而

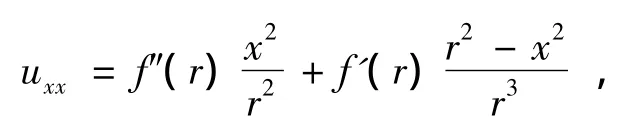
于是

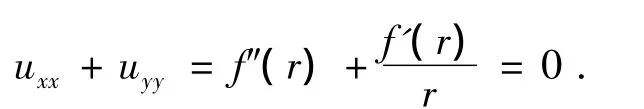
解得:

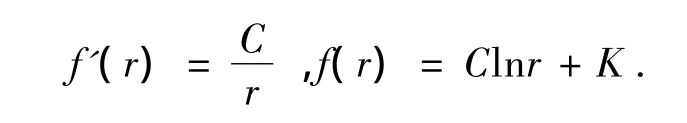
其他维度下类似可证.

特别地，当n=3时，仿照以上手法，可得u(x，y，z)=

若C≠0时，则此解在(0，0，0)无定义.因此，唯一处处有定义的球对称解是u=K，产生零万有引力(-▽K=0).当C≠0时，得到定义在不包含(0，0，0)的任意区域D上的解.

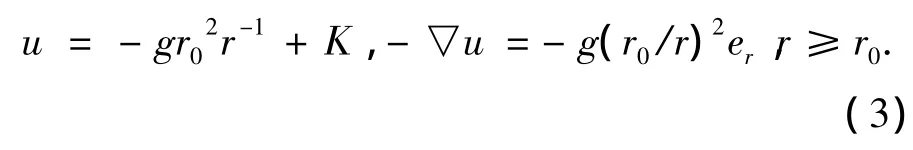
取D为某个外部孤立的行星，r＞r0.假设万有引力加速度的大小▽u=Cr-2等于行星表面的g(于地球而言g≈9.8 m·s-2)，则有或.于是其中，er是由 (0，0，0)指向外部的向量场.当r＜r0时，因为是行星内部ρ＞0，此时公式不可用.从(3)式中可以看到，▽u与r-2成正比，所以从Laplace方程推出了万有引力反比律.

注(逃逸速度):位势差u(∞)-u(r0)=gr0是将一单位质量物体从行星表面移动到空间任意远处所需的能量.因此，不计空气阻力，单位质量物体的动能作为发射物完全脱离行星所需的动能gr0.换句话说，逃逸速度的大小为对地球而言这个速度大约为11.2 km/s.

2 解的物理应用

一质量为m的行星以极坐标系在(r(t)，θ(t))处的角动量为mr2(其中)，它为某个常数，记为A，作为中心力.因此则行星的动能

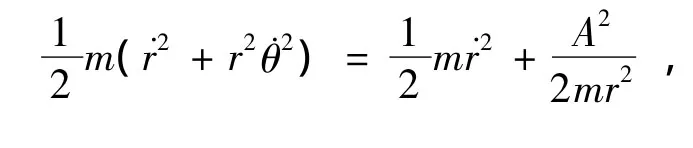
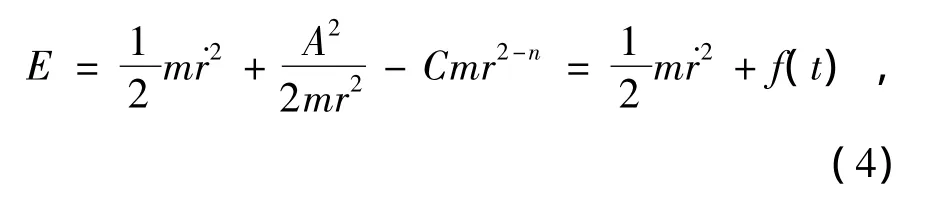
其中

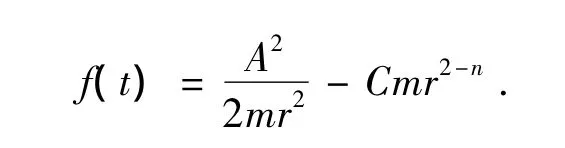
假设行星轨道对r至少有两个相邻的局部极值，设其为r1和r2(r1＜r2).当n=3时，这个假设是可能的，因为这时有椭圆轨道.

引理1 f(t)必在r1和r2之间的某点r0有严格小于E的局部极小.

证明在轨道的极值点处，有˙r=0.因此由(4)得

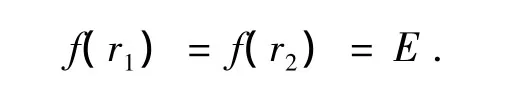
由于行星在这两个相邻的极值点之间运行时，

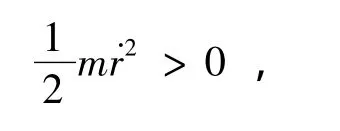
所以必有

f(r)＜E，r1＜r＜r2.

引理2 n=4时，不存在r0使得f'(r0)=0;除非f(t)≡E=0.

证明 当n=4时，

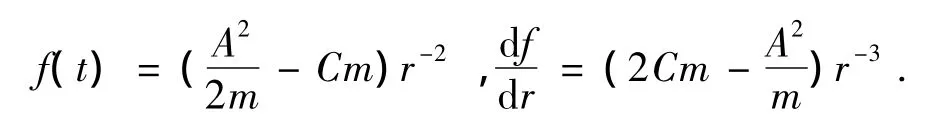
若存在r0使得f'(r0)=0，则必有

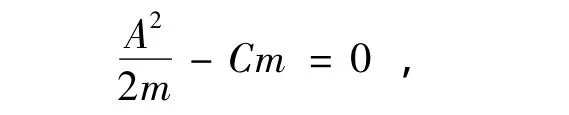
即有f(t)≡E=0.

引理3 n＞4时，存在唯一的正数r0，使f'(r0)=0，且该值是局部最大值.

证明 当n＞4时，

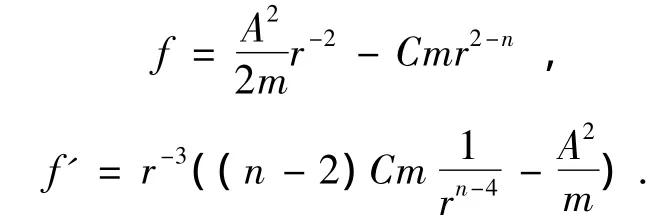
令f'=0，解得

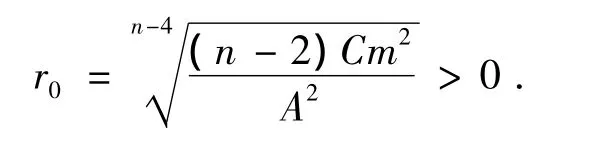
易得当r∈(0，r0)时，f'＞ 0;当r∈(r0，+∞)时，f'＜0.所以该值是局部最大值.

由上述引理可知，当n＞3时，行星轨道对r没有两个相邻局部极值.这时圆形轨道是有可能的，但这样的轨道是不稳定的，因为非常轻微的碰撞就会使行星偏离运行轨迹，从而有如下结论:

定理2 维数大于3的行星轨道是不稳定的.

［1］李俊杰.基础偏微分方程［M］.北京:高等教育出版社，2006:22－39.

［2］张洁，祝家麟，张凯.Laplace方程的 Galerkin边界元解法［J］.重庆大学学报，2003，26(10):39 －41.

［3］马荣.Laplace方程在静电场中的意义［J］.商丘师范学院学报，2003，19(2):131 －132.