无阻力任意摆角下配重复摆振动的数值研究

陈希明，潘娜娜，潘 宇

(重庆邮电大学数理学院，重庆 南岸 400065)

在小角度下从理论和实验方面研究配重复摆周期的变化规律是复摆研究问题中一项重要内容，在这些方面已经有不少报道［1－4］，其中文献［1－2］的研究方式较为相近，均从理论分析角度采用配重周期与无配重周期比率的方式，研究了周期随悬挂点及配重位置变化的规律，得到了较好的结果.在本文中，我们从匀质细杆加一配重的物理模型出发得到了任意摆角下配重复摆运动的微分方程.由于非线性效应，我们无法得到对应的解析解，因此很难了解配重复摆的运动图像.近年来，对物理问题进行数值研究［5－11］已经成为物理教学研究中普遍采用的方法.在本文中，我们首先对配重位置改变时的配重复摆的运动过程进行数值模拟并从中得到其周期;其次研究悬挂点和配重的位置固定下配重复摆的周期与角振幅的拟合关系，得到任意摆角配重复摆周期的拟合公式.为了验证该周期公式的正确性，我们比较了该式计算的任意摆角的周期和数值计算的结果.数值求解方法扩展了配重复摆的研究途径与方法，具有一定的应用价值.

1 模型及运动方程

如图1所示，忽略空气与轴的阻力下，配重复摆在绕悬挂点D摆动的过程中始终满足能量守恒方程:

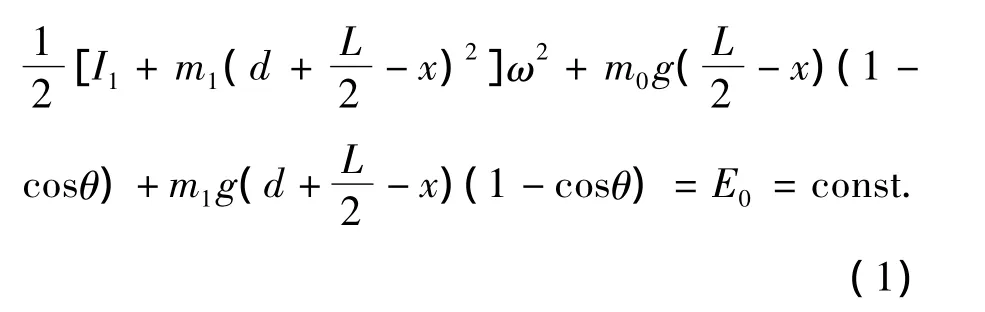
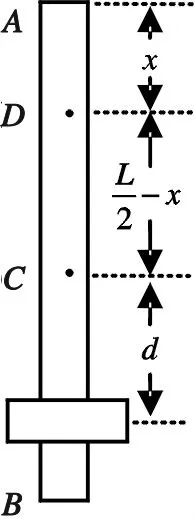
图1 配重复摆模型

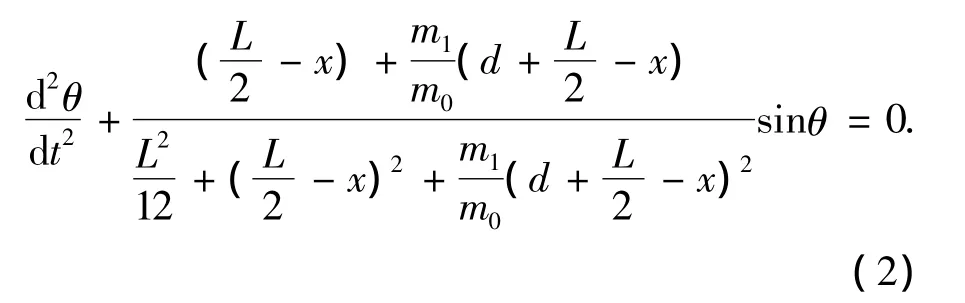
该式对任意摆角的配重复摆成立.当θ很小时，我们可以利用sinθ≈θ直接由(2)式得到配重复摆的周期T的平方值:

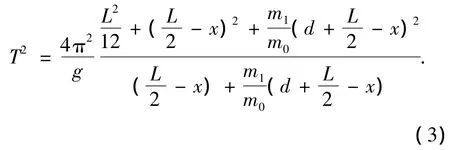
(3)式即为系统的固有周期.此时，配重复摆的周期仅与系统参数有关，即由摆长、配重所在位置、悬挂点位置以及配重与杆的质量比m1m0同时决定.但对于一般情况，我们很难从(2)式获得解析解，因此通常借助Mathematica等数学软件数值求解.在保持质量比不变的情况下，我们在本文中通过调节配重在匀质杆上的位置分别对 θ0≤5°，5°＜ θ0≤90°和90°＜ θ0＜180°范围内的运动过程进行数值模拟，并在固定悬挂点和配重位置的情况下研究配重复摆的周期与摆角的关系.

2 任意摆角下配重复摆运动过程的数值模拟

为简便起见，我们假设配重复摆悬挂在杆端A点处(即x=0)，并取均质杆长L=2.0m，线密度 λ =1.0 kg·m－1，重力加速度g=9.8m·s－2.在不同的初始条件下，我们利用Mathematica软件计算方程(2)得到复摆角位移θ(t)～t、角速度和角加速度的关系，如图2～图4所示.

利用Mathematica寻找函数全域最大值的方法，我们通过数值计算得到了配重位置改变时的系统周期，并将它与公式计算的结果进行比较，如表1～表3所示.表中的第一列代表不同的配重位置，第二列与第三列分别表示在相应配重位置时利用公式(2)与(3)计算的周期，第四列对应相应的误差.通过比较，我们发现随着配重位置从杆端A向杆端B的改变，不同摆角对应的配重复摆周期均增加，并且由于非线性振动，数值周期不仅与系统参数有关，还依赖于初始条件.图2～图4充分表明了这种变化与依赖关系，其中图2显示了在小角度下配重复摆微振动时各量随时间的变化关系.当摆角θ0≥5°时的大角度配重复摆运动的详尽分析，读者可参阅文献［12］.

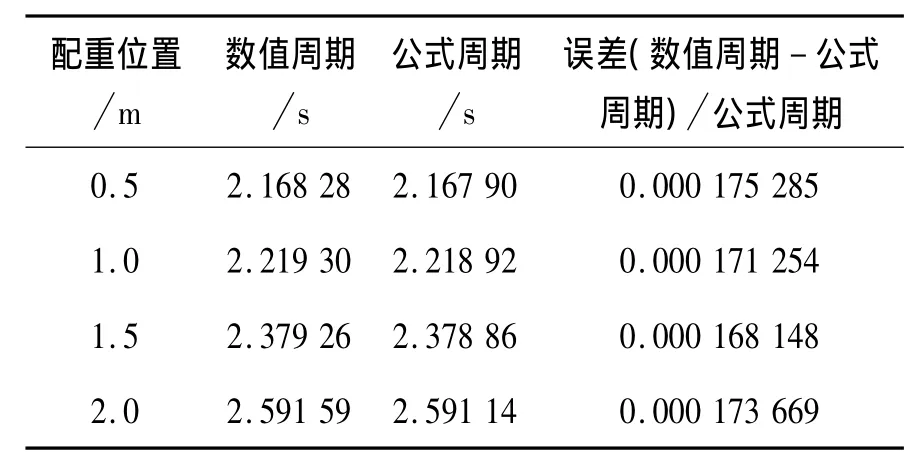
表1 在初始条件θ0=3°，ω0=0下配重位置改变时，数值计算周期与公式计算周期的对应关系

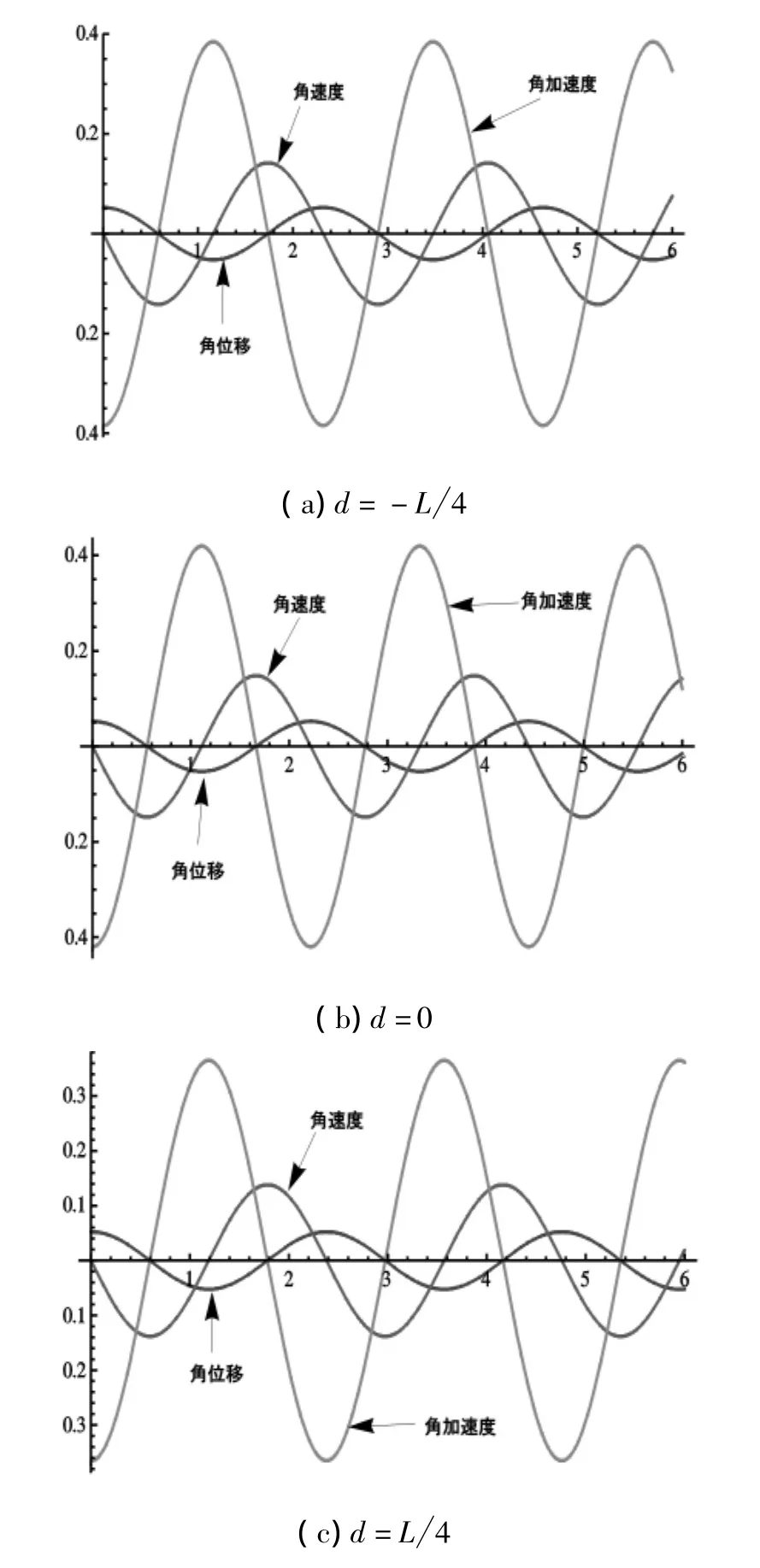
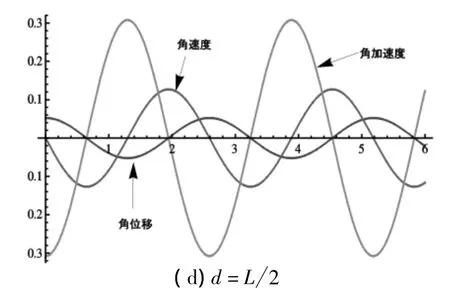
图2 θ0=3°，ω0=0配重处于杆的不同位置时，位移、角速度及角加速度之间的关系

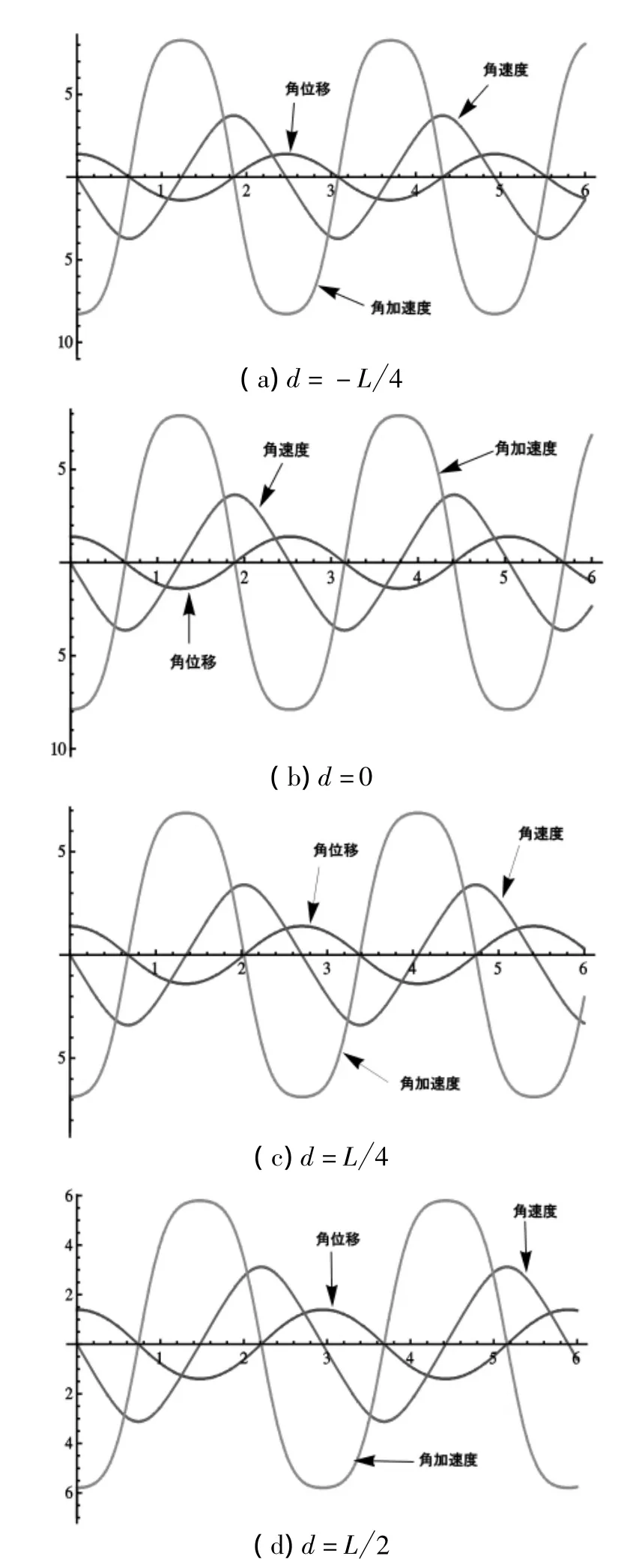
图3 θ0=80°，ω0=0配重处于杆的不同位置时，位移、角速度及角加速度之间的关系

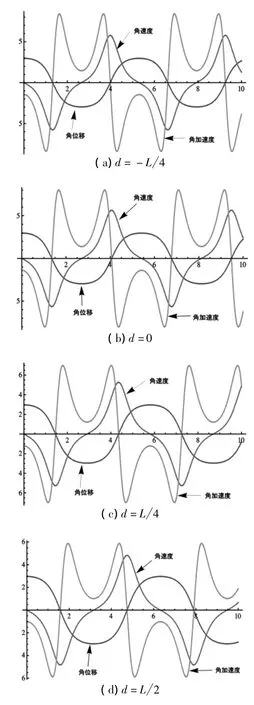
图4 θ0=170°，ω0=0配重处于杆的不同位置时，位移、角速度及角加速度之间的关系

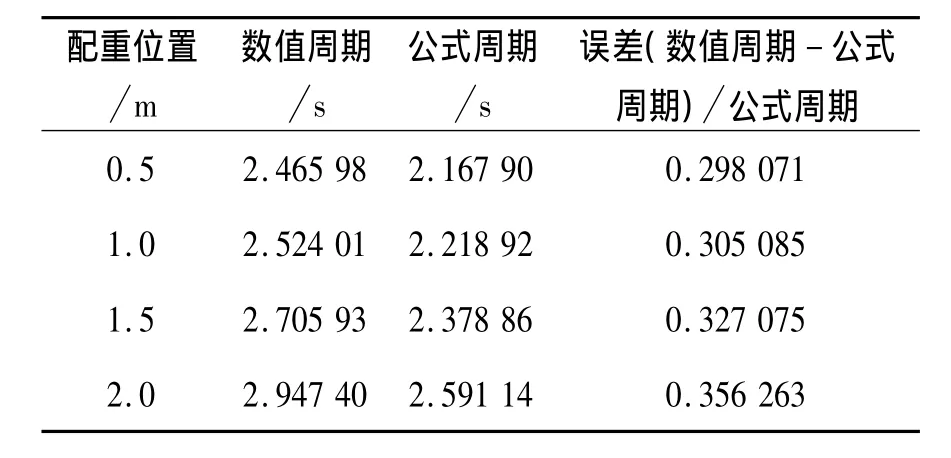
表2 在初始条件θ0=80°，ω0=0下配重位置改变时，数值计算周期与公式计算周期的对应关系

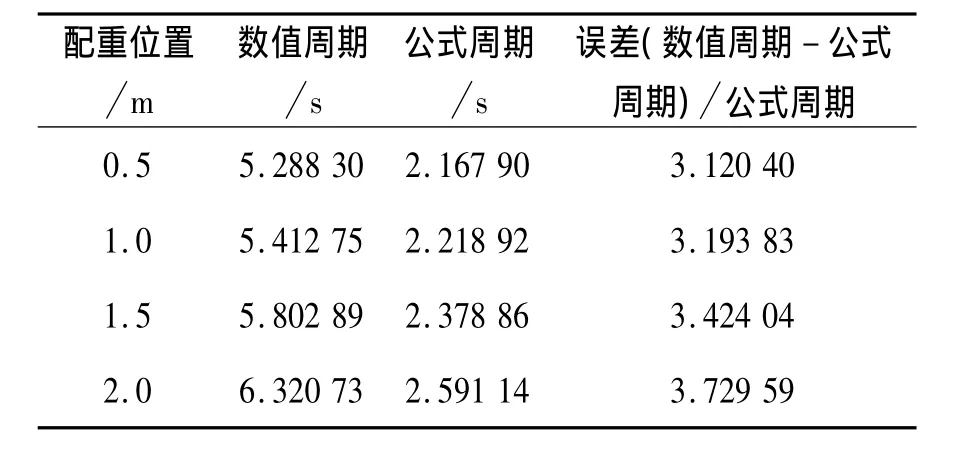
表3 在初始条件θ0=170°，ω0=0下配重位置改变时，数值计算周期与公式计算周期的对应关系

3 周期与角振幅的拟合

该部分我们利用Mathematica软件对方程(2)进行数值求解来详细研究配重复摆的周期与角振幅之间的关系.为简便起见，我们假设复摆绕端点A转动，并取 L=2.0 m，λ =1.0 kg·m－1，ω0=0.限于篇幅和讨论的相似性，我们仅讨论质量比m1m0不变且配重位置d=0的这种情况.通过循环语句Do［］使角振幅θ0从0.04 rad到1.6 rad逐渐增大，我们便可以得到不同角振幅对应的周期，最后利用线性拟合函数Fit［］对周期公式进行拟合.

图5显示了配重复摆振动周期与角振幅之间的关系，其中粗点表示不同角振幅下周期的计算值，曲线表示相应的拟合曲线.由此可见，两者吻合很好，且配重复摆的周期随着角振幅的增加而缓慢增大.

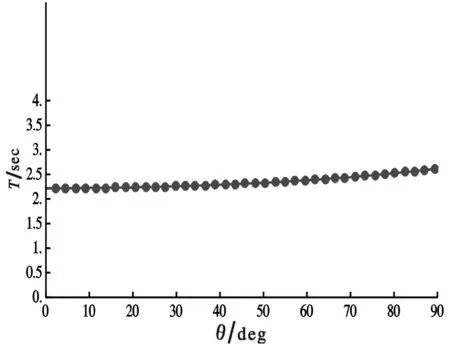
图5 配重复摆振动周期与角振幅的关系与拟合

我们得到的周期拟合公式为

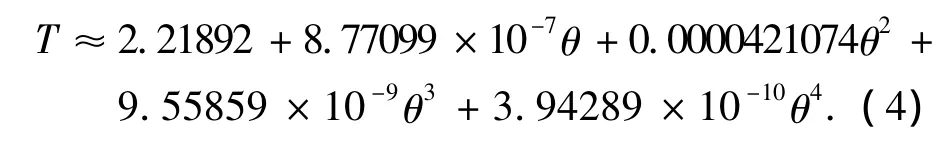
该式可用来计算任意角振幅下的振动周期.当θ=0时，复摆的周期值为2.218 92 s，它与公式(3)算出的结果相同，这说明周期拟合公式能正确给出小角度下的周期值.为了验证拟合公式的正确性，我们在表4分别列出了利用公式(2)与公式(4)得到的周期值.其中第二列表示由(2)式数值计算的周期，第三列则是由(4)式拟合的周期.通过对比，我们得出如下结论:1)复摆周期随着角振幅增大而增大，这是非线性效应影响的结果，增大的幅度从数值上能定量地看出来，比图5更为直观和明显;2)数值周期与拟合周期完全吻合，说明根据拟合公式计算的配重复摆周期具有很高的可靠性.

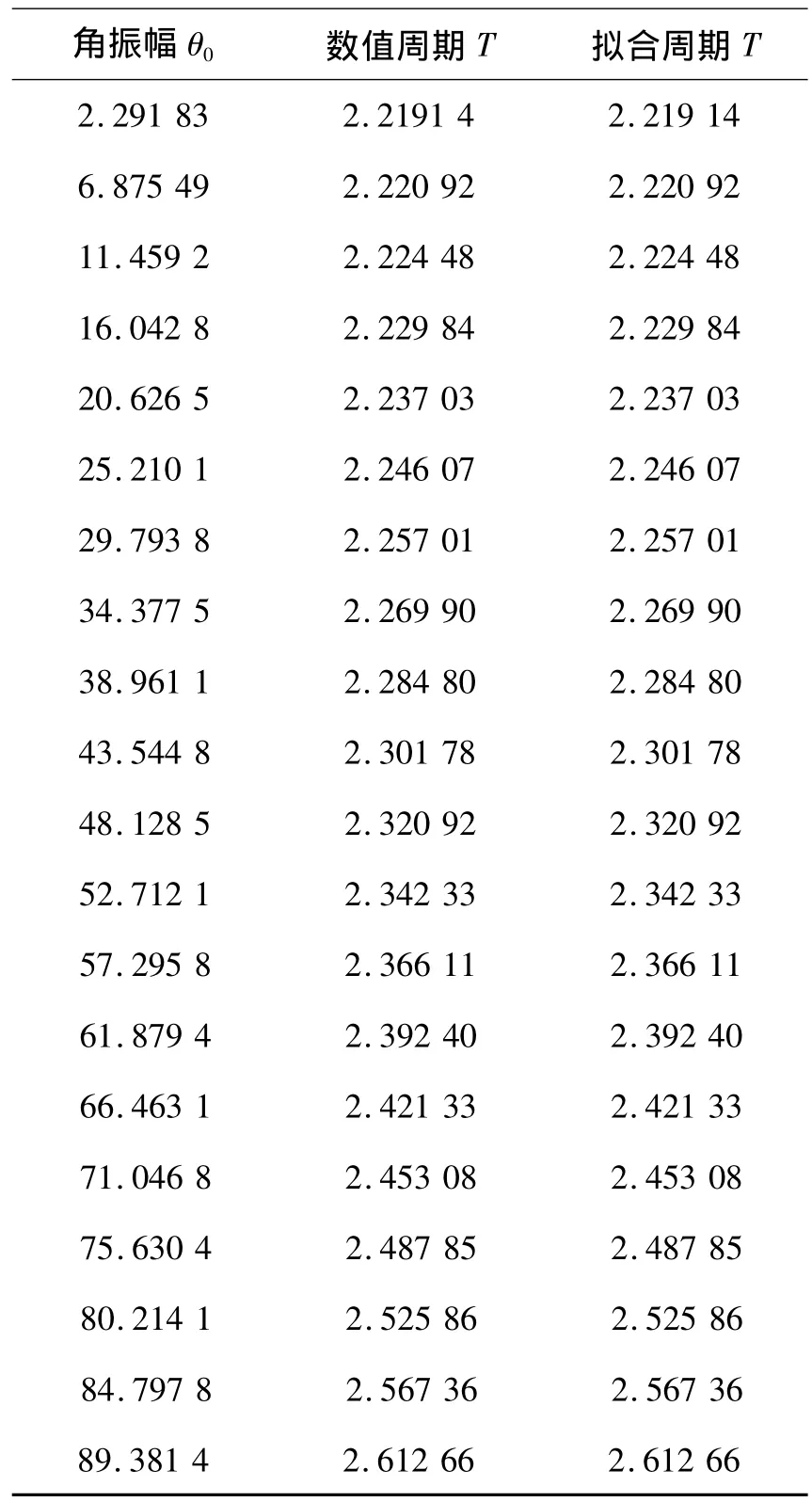
表4 角振幅逐渐增大下，数值计算周期和拟合公式计算周期的对比

4 结语

以匀质细杆加配重为物理模型，我们得到了配重复摆振动的非线性微分方程与周期的一般表达形式.在保持质量比m1m0=12不变的情况下，通过调节配重在匀质杆上的位置，我们对任意摆角配重复摆运动过程进行了数值模拟，比较了数值周期与公式周期的不同，发现随着配重位置从杆端A向杆端B的改变，任意摆角配重复摆的周期将增加.同时，我们还研究了悬挂点和配重的位置固定情况下配重复摆的周期与角振幅的拟合关系，得到了任意摆角配重复摆的周期拟合公式.为了验证该周期公式的正确性，我们利用拟合公式计算了任意摆角的周期，并与数值计算的结果进行了比较，发现根据拟合公式计算的配重复摆周期具有很高的可靠性.本文的研究表明数值求解方法可以扩展配重复摆的研究途径与方法，具有一定的应用价值.

［1］邹得滨，王艳辉，张天洋，等.加配重复摆振动周期变化规律的研究［J］.物理与工程，2008，18(6):13－15.

［2］任新成，王玉清，石延梅.加配重复摆振动周期的变化规律［J］.延安大学学报:自然科学版，2004，23(3):30－32.

［3］白泽生，刘竹琴.复摆加一配重后周期的变化［J］.延安大学学报:自然科学版，1997，16(4):87－88.

［4］张秀莲，林长.复摆设计的实验探讨［J］.西北师范大学学报:自然科学版，1996，32(3):79 －81.

［5］张东，曹胜亮.基于MATLAB的电容传感器动态特性分析［J］.重庆文理学院学报:自然科学版，2008，27(6):54－57.

［6］何玉平.MATLAB在大学物理中的应用［J］.重庆文理学院学报:自然科学版，2009，28(5):31 －34.

［7］鲍四元，孙洪泉，陈旭元.Mathematica在振动波问题中的应用［J］.物理与工程，2010，20(4):49 －51.

［8］于凤军，景义林.一个单摆周期近似公式［J］.大学物理，2007，26(5):18 －19.

［9］路洪燕，从守民，刘保通，等.Mathematica在大学物理教学中的应用［J］.淮北煤炭师范学院学报:自然科学版，2010，31(4):83 －86.

［10］任继阳，刘心益.运用Mathematica描绘光的多缝衍射图样［J］.玉溪师范学院学报，2011，27(4):61－64.

［11］樊东红，黄玛莉，柳继峰.利用Mathematica研究类圆孔和类圆环的夫琅禾费衍射［J］.河南师范大学学报:自然科学版，2008，36(4):80 －82.

［12］邹芳红，崔百宁.大角度复摆的运动方程［J］.物理通报，1999(4):26－27.