基于频率灵敏度方法的超声键合换能器结构优化

隆志力 韩 雷 祝孟鹏 张亮亮

1.哈尔滨工业大学深圳研究生院，深圳，518055 2.中南大学，长沙，410083 3.东莞华中科技大学制造工程研究院，东莞，523808

0 引言

超声换能器是应用压电陶瓷材料具有的压电效应，将电能量转化为高频率超声波能量的一种智能装置。目前，超声换能器已经广泛应用于国民生产的各个领域，如工业焊接、水声、环保、医疗等，成为工程装备中重要的核心执行机构［1－2］。

在当前我国日趋被重视的半导体工艺与设备中，芯片键合换能器是被公认的超声键合装备的关键部件之一［3－5］，其主要作用是为细微金属引线（如金线、铝线、铜线）与基板相互连接提供必需的超声能量，实现半导体器件IC或LED芯片的信号传递。虽然在结构组成上，键合换能器与其他工业领域的压电换能器类似，但其工作的对象与条件更为苛刻，表现为：金属引线的直径为12.5～25.0μm，环境温度约200℃，换能器运动加速度高达约20g，且通常情况下换能器保持24h连续工作。因此，这些特殊的键合条件与因素对超声换能器的能量稳定性与精确控制都提出了很高的要求。

当前对超声换能器的研究大多集中于设计方法与过程，包括有限元、等效电路方法、传递矩阵方法等［6－8］。国内外对换能器性能优化的研究鲜有报道。事实上，基于以上方法设计的换能器在频率与振动模态上经常存在诸多问题，如频率漂移、模态混叠、模态畸变、阻抗过高等［9－10］。因此，优化超声换能器性能对提高其自身的能量传递效率具有重要意义。本文针对超声键合换能器设计中存在的模态混叠现象，研究了其结构优化与控制方法，并用相关试验进行了验证。

1 超声键合换能器的模态混叠现象

超声键合换能器主要由前盖板、后盖板、压电陶瓷、变幅杆等部分组成，如图1所示。在超声发生器的驱动下，压电陶瓷通过逆压电效应将电能转换为轴向机械振动，经由变幅杆的位移放大作用，将超声能量传递到芯片键合界面。

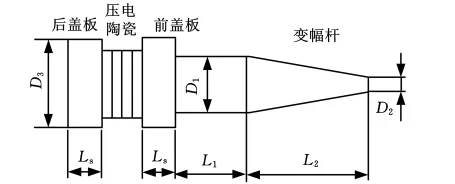
图1 超声键合换能器结构

表1与表2为一组超声键合换能器的主要材料参数与主要尺寸。利用美国Agilent公司4294A阻抗分析仪扫频实测该换能器的频率与导纳特性，测试条件为：起始频率55kHz，终止频率70kHz，频率间距5Hz。测试结果如图2、图3所示。由测试结果可知：在55～70kHz范围内，该换能器的工作频率为61.680kHz，此时系统阻抗为最小值；此外，换能器还包含57.452kHz干扰频率。从导纳上可发现，此时换能器有两个频率的导纳圆混杂在一起。因此，工作频率与干扰的非工作频率相互接近，造成实际工作中超声驱动电源有可能跟踪在干扰频率点上，或者在工作频率与干扰频率之间相互切换，导致换能器的超声能量输出不稳定。

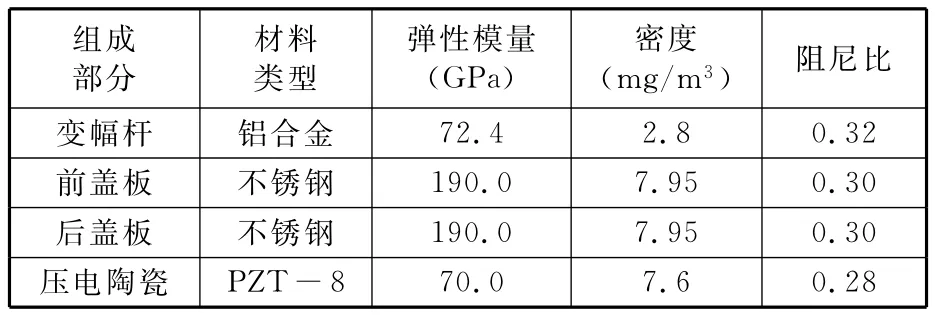
表1 超声键合换能器主要材料参数

表2 超声键合换能器主要尺寸 mm

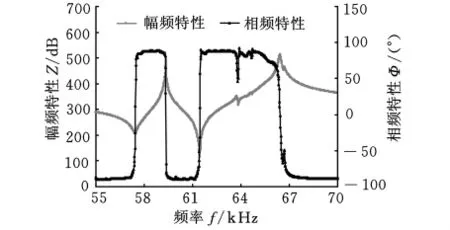
图2 换能器优化前的频率特性

利用有限元方法计算该超声换能器的固有频率与振动模态，采用的商业软件为ANSYS 9.0，模型包含12 430节点，8149单元，采用Block Lanczos计算方法进行计算。结果表明，在56～65kHz范围内，换能器包含3阶固有振动模态，即61.399kHz轴向模态、59.824kHz垂直弯曲模态、62.563kHz水平弯曲模态，如图4～图6所示。可以发现，各阶模态混叠在一起，在超声发生器频率跟踪精度有限的情况下，这些模态都有可能被激发，产生多模态效应。

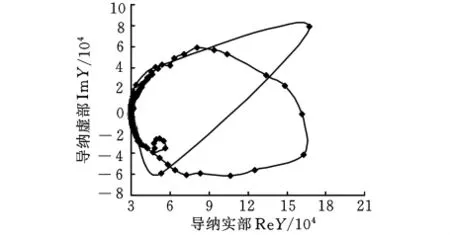
图3 换能器优化前的导纳圆

图4 轴向模态（频率为61.399kHz）

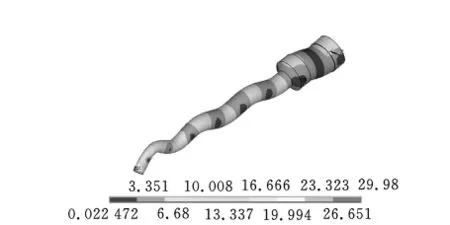
图5 垂直弯曲模态（频率为59.824kHz）

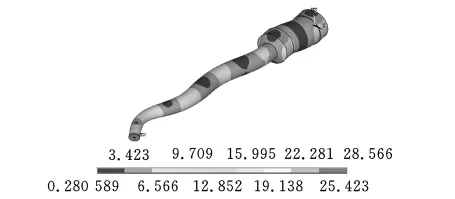
图6 水平弯曲模态（频率为62.563kHz）

2 优化方法与过程

2.1 频率灵敏度方法

设换能器的任一结构参数为pj（j＝1，2，…），换能器第r阶模态的固有振动方程为［11-13］

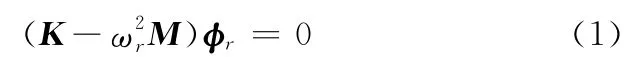
式中，K为系统刚度矩阵；M为系统质量矩阵；φr为第r阶振型矩阵；ωr为第r阶模态频率。

对式（1）求偏导数，并利用振型与质量矩阵归一化的关系，得到模态频率对结构参数的灵敏度：

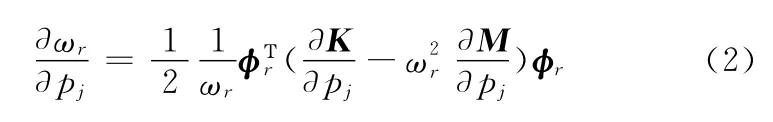
考虑到换能器结构参数pj的大小相差较大，采用相对灵敏度：

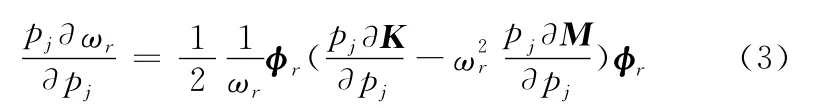
采用差分近似可得：

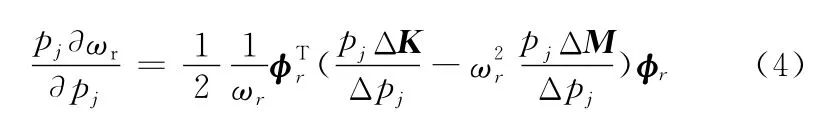
式中，Δpj为结构参数pj的变化量；ΔK为系统刚度矩阵的变化量；ΔM为系统质量矩阵的变化量。

因此，给出结构参数pj的一个摄动量，通过有限元模型计算摄动后的刚度矩阵和质量矩阵的变化量ΔK和ΔM，由式（4）可求得模态频率对某一结构参数pj的相对灵敏度。

2.2 优化过程

基于上述频率灵敏度方法，对换能器有限元模型进行各结构参数摄动，即各结构尺寸变化量为±1%，提取模型变化前后的刚度与质量矩阵差（即ΔK和ΔM）以及各阶模态的振型（即φr），代入模态灵敏度计算公式（式（4）），可得各模态频率对结构参数的灵敏度，计算结果如图7所示。可以发现，轴向振动模态对结构参数D1（即变幅杆直径）的灵敏度不大，而其他模态对变幅杆直径D1的灵敏度很大。因此，适当调节结构参数变幅杆直径D1，可以有效地将轴向模态与其他非轴向模态分离。

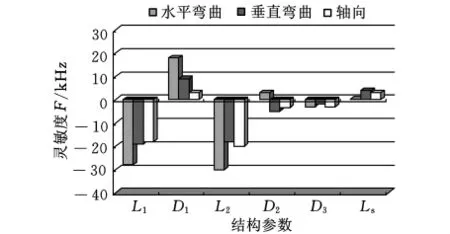
图7 各频率对结构参数的灵敏度

3 优化结果与验证

对于超声键合工艺，换能器的工作模态与非工作模态之间频率间隔控制在3kHz范围之外为最优。将变幅杆直径D1从7.8mm调节到8.5mm，利用有限元方法计算优化之后的系统振动模态，结果如图8～图10所示，此时工作频率与非工作频率最小间隔为3.408kHz。由此可得，微调变幅杆直径D1，可将水平弯曲和垂直弯曲的非轴向工作模态从55～65kHz范围内分离出来，保证超声发生器频率跟踪范围内只存在唯一的工作频率，使得换能器单一的工作模态被激励成为可能。

图8 优化后轴向模态（频率为61.989kHz）

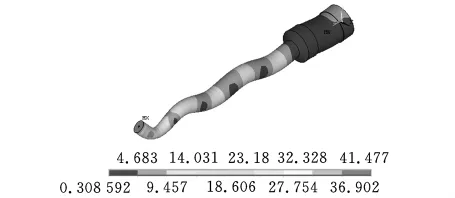
图9 优化后垂直弯曲模态（频率为54.266kHz）

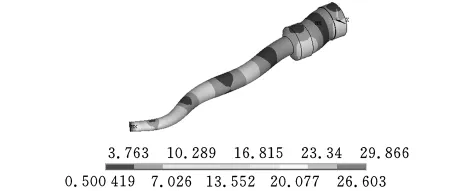
图10 优化后水平弯曲模态（频率为65.397kHz）

将变幅杆直径D1改变之后，对换能器的频率与导纳特性进行测试验证。图11、图12为实测结果，可以发现，优化之后的换能器在55～65kHz范围内只有唯一的轴向频率，导纳圆也近似为单一的圆形，表明换能器工作频率附近杂散的干扰频率得到有效抑制，保证了换能器在一定范围内只存在单一纯净的轴向工作频率。

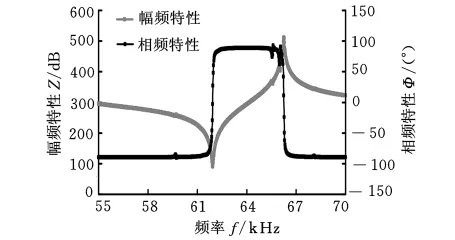
图11 换能器优化后的频率特性

4 结束语

针对超声换能器设计上存在的模态混叠问题，采用模态频率灵敏度的方法，通过结构优化，实现了换能器工作频率与非工作频率的分离，有效地控制了换能器模态混叠的现象。以61kHz芯片键合换能器为对象，使用阻抗分析仪和有限元方法相结合，均发现换能器在61kHz工作频率附近存在明显的模态混叠现象，依据模态灵敏度的计算结果，通过最小量地改变变幅杆直径，有效地将水平与垂直弯曲等非工作模态从轴向工作模态中分离出来，保证换能器工作频率附近没有存在其他杂散的干扰频率，使得工作过程中换能器被驱动在唯一的工作频率点，从而提高了换能器超声能量输出的稳定性。

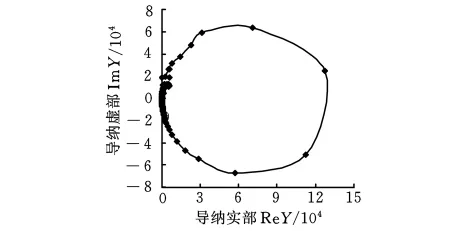
图12 换能器优化后的导纳圆

［1]冯若.超声手册［M］.南京：南京大学出版社，2001.

［2]袁易全，陈思忠.近代超声原理与应用［M］.南京：南京大学出版社，1999.

［3]Rao R T.Microelectronics Packaging Handbook［M］.New York：Mcgraw－Hill Publisher，2001.

［4]Long Zhili，Han Lei，Wu Yunxin，et al.Dynamics of Ultrasonic Transducer System in Thermosonic Flip Chip Bonding［J］.IEEE Components and Packaging Technology，2009，32（2），261－267.

［5]周铁英.超声键合换能器的研究——回顾与展望［J］.声学技术，2006，25（3）：258－262.

［6]吴运新，隆志力，韩雷，等.芯片键合换能器研究现状分析 ［J］.中 国 机 械 工 程，2008，11（19）：1371－1378.

［7]隆志力，吴运新，韩雷，等.热超声键合换能器阻抗／导纳模型［J］.机械工程学报，2007，43（10）：14－19.

［8]赵福令，冯冬菊，郭东明.超声变幅杆的四端网络法设计［J］.声学学报，2002，27（6）：554－558.

［9]赵向东，袁义坤，赵淳生.超声电机定子的有限元分析及其模态混叠现象［J］.振动工程学报，2004，17（S）：705－868.

［10]周光平，梁明军，王家宣.大尺寸超声振动体的研究［J］.声学技术，2004，23（3）：183－190.

［11]曾劲松，陈超，赵淳生.超声电机两相模态频率一致性调节的方法［C］／／全国第三届超声波理论和应用技术研究会论文集.杭州，2005：133－137.

［12]闻邦椿，刘树英，何勍.振动机械的理论与动态设计方法［M］.北京：机械工业出版社，2001.

［13]朱华，曾劲松，赵淳生.杆式超声电机定子的动力学分析与优化设计［J］.中国机械工程，2008，19（21）：2627－2632.