半滑动式液压胀形汽车桥壳的数值模拟及成形实验
梁 晨 刘唯唯 陈国强 苏明凯 王连东
燕山大学,秦皇岛,066004
0 引言
汽车桥壳属异型截面复杂管类件,要求有较高的强度和刚度。用液压胀形方法制造汽车桥壳,比铸造方法节省材料,与冲压焊接方法相比,工序简单,材料利用率高,且壁厚变化合理。
关于轴对称管件液压胀形的研究较多。Shirayori等[1]研究了管坯的壁厚偏差及材料性能参数对液压胀形的影响,通过实验与有限元模拟得出:胀形中管坯壁厚的变化量取决于初始的管坯壁厚偏差和材料的硬化指数n及各向异性系数r,初始壁厚偏差大而n、r小时,壁厚偏差增加值大。文献[2-4]研究了加载路径对液压胀形的影响,其中,Aue-u-Lan等[4]通过对不同材料管件液压胀形的有限元模拟及实验验证,研究了加载路径(轴向进给与胀形压力的关系)对液压胀形的影响,认为有限元模拟可以确定管件液压胀形的最佳加载路径,可以提高生产率,减少错误。Nikhare等[5]得到了不同加载条件下管件液压胀形的极限变形,并将其与板胀形、板冲压的极限变形进行了比较。上述研究使用固定式液压胀形,在胀形过程中,模具固定不动,通过管坯端部施加设备的轴向推力。
汽车桥壳的截面形状复杂,采用液压胀形工艺制造时,桥包部位胀形量大,而使用固定式液压胀形方式,模具给管坯的轴向推力不能有效作用于胀形部位。20世纪80年代,日本学者用滑动式液压胀形方法试制出微型汽车桥壳样件[6],在工艺技术上取得了一些宝贵经验,但该工艺所需设备吨位相对过大,不适合制造大型桥壳,未见该工艺的后续研究报道。21世纪初,Lei等[7]对微型汽车桥壳的液压胀形过程进行了数值模拟,燕山大学在汽车桥壳滑动式液压胀形的工艺理论、实验装置等方面进行了一定的研究[8-9]。
本文针对某小型汽车桥壳的半滑动式液压胀形工艺,运用ANSYS软件进行成形过程的数值模拟,分析不同加载路径下的管坯成形情况及其壁厚分布,确定出较好的加载路径,并在普通液压机上试制出小型汽车桥壳样件。
1 研究对象
燕山大学液压胀形课题组在固定式液压胀形工艺(图1a)和滑动式液压胀形工艺(图1b)的基础上,提出适合胀形大型复杂截面管类件的半滑动式液压胀形工艺,假想将制件沿轴向分成中间部分与左右两部分,相应地将胀形模具成形部分设计成3个模块(图1c)。左右模块可水平滑动,其作用是带动管坯相向运动实现轴向补料;中间固定模块由可分开的两部分组成,其作用是控制管坯中部胀形的大小,固定模块两部分分开后可方便取件。采用半滑动式液压胀形工艺,滑动模块将轴向推力有效施加在管坯上,同时承受了管坯胀形时的大部分内力;中间固定模块将管坯中间的悬空长度L均匀分布在两侧(图1c),可控制管坯胀形大小,防止管坯在合模前胀出模具型腔而出现飞边。
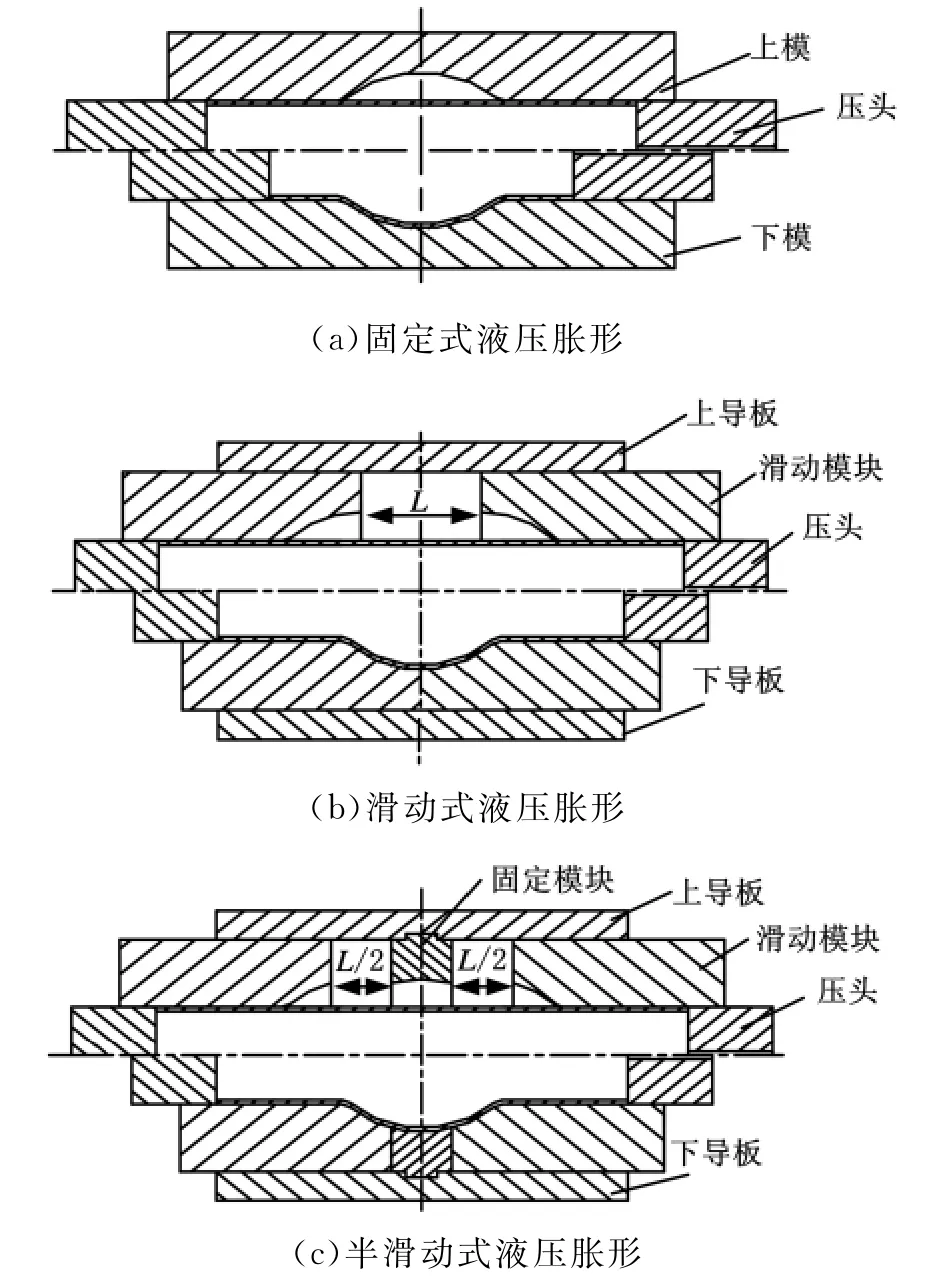
图1 管坯液压胀形方式
本文采用半滑动式液压胀形工艺在普通液压机YA315上试制的桥壳总长为1050mm,中间截面最大高度(当量直径)为212mm,两端直臂圆管部分的外径为67mm,受到液压机开间的限制,将原桥壳两端直臂部分长度分别缩减287mm,桥壳样件总长度为476mm。参照样件尺寸,建立的样件及预胀形管坯的三维模型如图2所示。
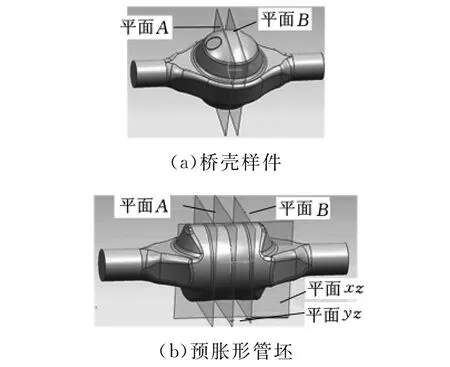
图2 终胀形及预胀形管坯三维模型
预胀形管坯的三维模型如图2b所示,其中部呈凹曲面状:曲率半径R1=180mm,谷底直径为156mm,谷顶直径为162mm,端部与终胀形模具形状相同。图2中,平面A与平面B将样件(或管坯)分成三部分,相应地将胀形模具分为3个模块:中间为固定模块,左右为滑动模块。
选用初始直径为102mm、壁厚为5.5mm的20无缝钢管进行胀形,该钢管的屈服极限σs=350MPa,强度极限σb=420MPa,延伸率δ=30%,硬化指数n=0.2。管坯初始长度确定为558mm(图3a),两端部分(长度为119mm)缩径后的直径减为67mm,壁厚增至6.2mm,两端缩径后管坯总长度变为591mm,中间未缩径部分长度为320mm(图3b)。第一次胀形时,管坯轴向被压缩85mm,同时液压胀形,胀形后最大直径为162mm,中间截面直径为156mm(图3c);第二次胀形时管坯轴向被压缩30mm,同时液压胀形,胀形后管坯总长度变为476mm,中间截面最大直径为212mm(图3d)。

图3 某小型汽车桥壳液压胀形工艺
2 预胀形的数值模拟
2.1 有限元模型
利用有限元分析软件ANSYS建立有限元模型。基于预胀形管坯的几何对称性和胀形过程中载荷作用的对称性,只建立管坯和模具的1/4模型,如图4所示。采用Solid45单元对桥壳划分网格,在管坯与模具有可能接触到的平面建立刚性接触对,设定摩擦因数为0.03。由于管坯模型的左断面和下断面均为对称面,故施加对称约束;固定模块在胀形过程中保持位置不变,加全约束。通过滑动模块施加轴向位移载荷,同时在管坯内表面施加与液体压力相应的面载荷来模拟胀形过程。

图4 预胀形有限元模型
2.2 加载路径
预胀形分别采用4种路径加载,加载路径即管坯内液体压力p与模具对管坯的轴向压缩量s的关系如图5所示。路径1:管坯轴向进给过程中,内压保持37MPa不变,合模后内压升至60MPa。路径2:管坯轴向进给过程中,内压从37MPa线性增至42MPa。路径3:管坯轴向进给20mm过程中,内压保持37MPa不变,继续进给时,内压从37MPa线性增加至42MPa。路径4:管坯轴向进给40mm过程中,内压保持37MPa不变,继续轴向进给时,内压从37MPa线性增加至42MPa。
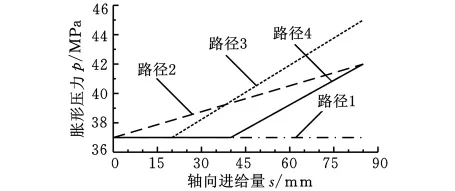
图5 预胀形加载路径
2.3 数值模拟
(1)管坯外形。按路径1加载,首先得到外形为双鼓形的管坯,中间截面最小直径为125mm,如图6所示。在无轴向进给情况下,内压升至60MPa,使管坯完全贴模,胀形后管坯外形如图7所示。

图6 双鼓形仿真样件
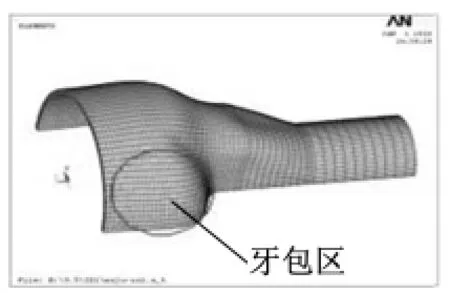
图7 预胀形样件
按图5所示的4种加载路径分别进行液压胀形,均可得到图7所示的管坯外形,且胀形过程中均无褶皱、胀裂现象出现。4种加载路径胀形过程中,管坯不同部位的贴模次序不同:按路径1、路径2加载,内压相对较高,牙包区贴模较早,如图7所示;按路径3、路径4加载,内压相对较低,牙包区贴模较晚。4种加载路径下都能得到比较满意的外形尺寸,成形稳定性好。
(2)壁厚分布。测量圆周方向上90°(z轴正向)至180°(x轴负向)的范围内每对节点处管坯的壁厚,如图8a所示;沿管坯轴向将管坯剖开,按从左到右的顺序测量每对节点的壁厚,如图8b所示。图5中的4种加载路径下的管坯胀形区壁厚分布如图9中的曲线1、2、3、4所示。
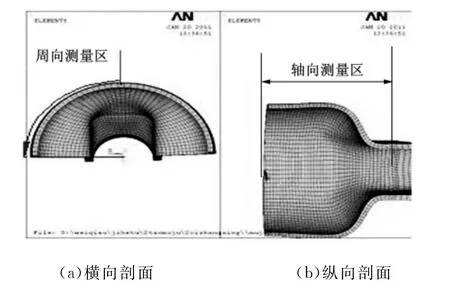
图8 预胀形样件剖视图

图9 预胀形样件壁厚分布
预胀形后管坯胀形区壁厚有不同程度的减小,由图9可知,加载路径1与其他加载路径相比有如下特点:
(1)管坯中间截面壁厚较大,且沿圆周分布较均匀:最厚为4.68mm,最薄为4.42mm,相差5.88%。加载路径2下的管坯,壁厚的最大值为4.56mm,最小值为4.03mm,相差13.15%。
(2)轴向壁厚分布相对较好。按路径1、2、3、4加载,得到的管坯纵向剖面上壁厚最小值依次为4.55mm、4.46mm、4.46mm、4.41mm。
(3)需要的胀形压力较高。路径1下管坯贴模需要的胀形最高压力为60MPa,而其他三种路径为42MPa。
综合分析4种加载路径对管坯壁厚的影响可得:胀形初期内压越高,管坯贴模越早,轴向进给的作用效果越差,中间截面壁厚越小;胀形过程中,应使管坯内压与轴向进给合理匹配,得到有益褶皱,合模后再通过高压来消除褶皱,使管坯壁厚均匀、减薄率小。
3 终胀形过程的数值模拟
终胀形(第二次胀形)是在第一次胀形且退火后进行的,数值模拟仿真中处理退火是通过管坯更新模型来完成的。终胀形模具的型腔与桥壳成品的外形一致,如图10所示;单元类型、材料属性、摩擦因数以及约束条件与第一次胀形相同。终胀形过程中模具轴向推进30mm,胀形系数为1.36。
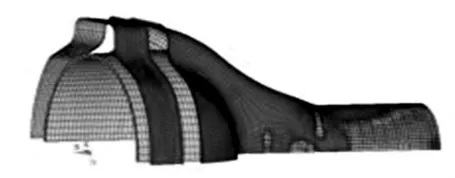
图10 终胀形有限元模型
终胀形时采用如图11所示的3种路径加载:按路径1加载,模具轴向推进过程中,内压保持25MPa不变直到合模;按路径2加载,模具轴向推进过程中,内压按线性关系从20MPa增至120MPa;按路径3加载,模具轴向在开始推进20mm的过程中,内压保持20MPa不变,继续推进时内压按线性关系从20MPa升至120MPa。

图11 终胀形加载路径
路径1下得到的试样外形见图12a,两个牙包成形不饱满:沿轴向,牙包的边缘A区和B区出现严重塌陷;沿圆周方向,C区和D区的圆角半径较大,没有贴模。路径2下得到的试样见图12b,由于压力过高,出现飞边,因此牙包也有明显压痕。路径3下得到的桥壳试样如图12c所示,两侧牙包成形饱满,胀形区处垂直于管坯轴线方向截面上的小圆角成形较好。

图12 终胀形后样件外形图
比较3种加载路径可知:终胀形采用路径3的分段线性加载,可制造出合格样件。出现塌陷的原因是管坯内压过低,管坯胀形时不能贴模;出现飞边的原因是管坯内压过高,管坯在滑动模与固定模合模前,部分金属从两模具间的间隙中胀出,该胀出部分在滑动模块与固定模块合模时被两模具压成飞边。按图11路径3得到的终胀形样件的壁厚分布如图13所示,周向壁厚测量与轴向壁厚测量的方法与预胀形测量壁厚的方法相同。
4 成形实验
4.1 胀形模具
利用普通液压机实现液压胀形时,预胀形中使用的模具结构如图14所示。模具成形部分由上模7、下模2、固定模块5三部分组成,其型腔分别对应图3b中预胀形管坯A平面以左部分、B平面以右部分以及A平面、B平面之间部分。固定模块5沿过轴线平面切分成两半,胀形后可分开便于取件。终胀形模具结构与预胀形类似,按图3a所示的制件外形设计模具型腔,固定模块模5的高度变为50mm。
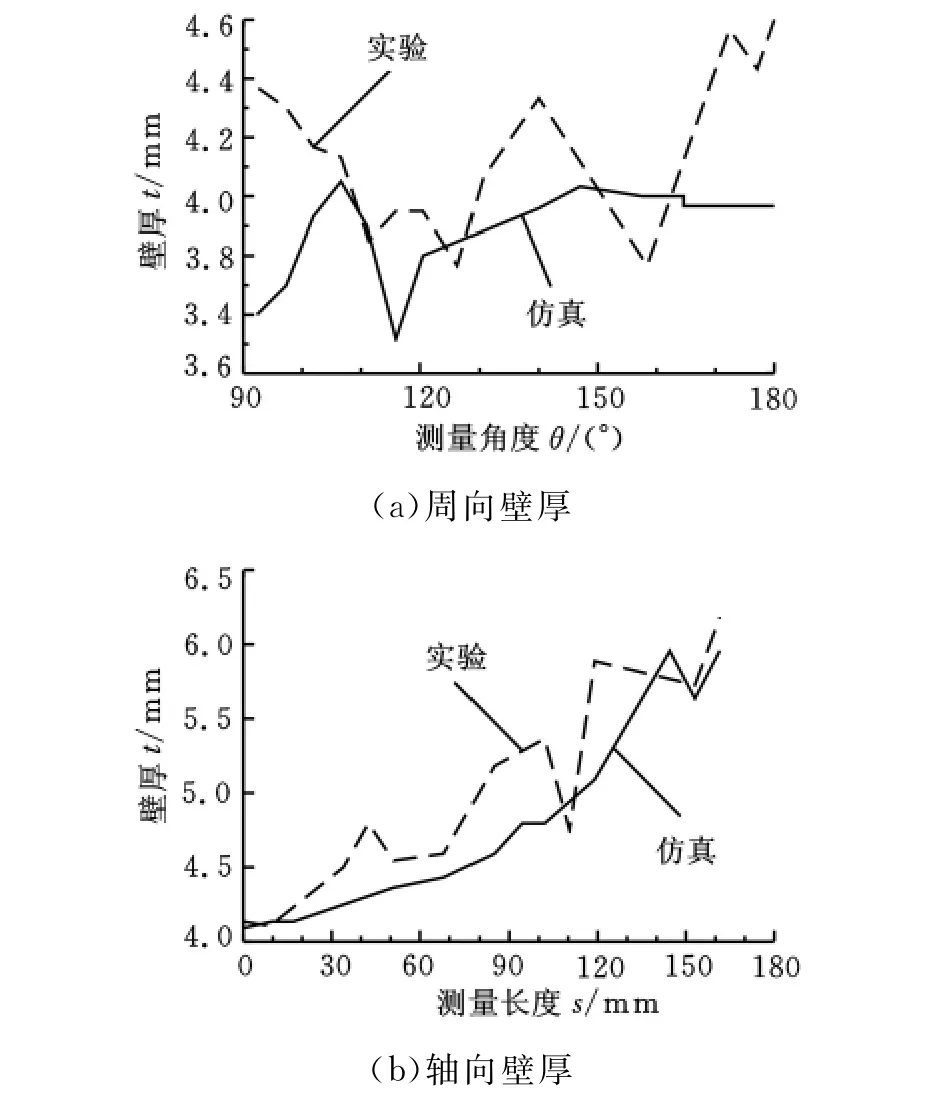
图13 终胀形样件壁厚分布

图14 液压胀形汽车桥壳预胀形模具
4.2 预胀形实验
按图5中的路径1加载,首先得到的双鼓形样件,如图15a所示,合模后使内压升到60MPa,得到预胀形样件。将样件沿轴向和周向切去1/8,如图15b所示。在周向及轴向上分别取20个均布的测量点,点之间的间隔为5.5mm,测量其壁厚,壁厚分布曲线亦绘于图9中。
比较路径1得到的仿真样件与实验样件的壁厚分布可知,实验样件壁厚与模拟值存在一定误差:圆周方向上,壁厚最小值为4mm,比模拟时的最小值4.45mm小10.11%;壁厚最大值为4.97mm,比模拟时的最大值4.68mm大6.20%。沿轴向,实验样件的壁厚分布与模拟结果趋势相同,但实验值与模拟值最大相差10.20%,实验值与模拟值的壁厚之差主要在于:实验用管坯为冷轧无缝钢管,在圆周方向上的初始壁厚不均匀,而数值模拟时设定了均匀初始壁厚;冷轧用无缝钢管材料在轴向与周向具有各向异性,数值模拟时将它们设置的各向同性。

图15 预胀形样件
4.3 终胀形实验
按图11路径3加载得到的合格样件如图16a所示,将样件沿纵向和周向切去1/8,如图16b所示。在周向及轴向上分别取20个均布的测量点,点之间的间隔分别为8mm、8.5mm,测量结果见图13。

图16 终胀形样件
对实验结果与仿真结果进行比较分析可知,样件周向及轴向上壁厚分布趋势相同:圆周方向壁厚最小的部分均出现在牙包边缘处,即当量直径最大的部分,实验值为3.74mm,比模拟值3.49mm大7.16%;沿轴向方向,实验值与模拟值的最大偏差均小于8%。
5 结论
(1)通过有限元模拟,得到了预胀形管坯壁厚分布较好的加载路径:管坯轴向进给过程中,内压保持不变,合模后增加内压成形。得到了终胀形时可确保成形合格样件的加载路径:胀形初期,液体压力先保持不变,轴向进给量达到2/3后再线性增加至终了压力。
(2)通过对比分析相同加载路径下实验样件、模拟样件成形情况以及在轴向、周向剖面上的壁厚值可知,模拟结果与实验结果趋势大体相同。鉴于实验用管坯壁厚存在偏差以及实验中液体压力存在一定波动,故实验样件壁厚结果与模拟值存在一定偏差。
[1]Shirayori A,Fuchizawa S,Ishigure H,et al.Deformation Behavior of Tubes with Thickness Deviation in Circumferential Direction during Hydraulic Free Bulging[J].Journal of Materials Processing Technology,2003,139(1/3):58-63.
[2]Koc M.Investigation of the Effect of Loading Path and Variation in Material Properties on Robustness of the Tube Hydroforming Process[J].Journal of Materials Processing Technology,2003,133(3):276-281.
[3]Bakhshi-Jooybari M,Elyasi M,Gorji A.Numerical and Experimental Investigation of the Effect of the Pressure Path on Forming Metallic Bellows[J].Journal of Engineering Manufacture,2010,224(1):95-101.
[4]Aue-u-Lan Y,Ngaile G,Altan T.Optimizing Tube Hydroforming Using Process Simulation and Experimental Verification[J].Journal of Materials Processing Technology,2004,146(1):137-143.
[5]Nikhare C,Narasimhan K.Limit Strains Comparison during Tube and Sheet Hydroforming and Sheet Stamping Processes by Numerical Simulation[J].Computers,Materials and Continua,2008,7(1):1-8.
[6]Terumori U.Differential Gear Casting for Automobiles by Liquid Bulge Forming Processs[J].Sheet Metal Industries,1983,60(4):220-222.
[7]Lei L P,Kim J,Kang B S.Analysis and Design of Hydroforming Process for Automobile Rear Axle Housing by FEM[J].International Journal of Machine Tools &Manufacture,2000,40(12):1691-1708.
[8]王连东,程文冬,梁晨,等.汽车桥壳液压胀形极限成形系数及胀裂判据[J].机械工程学报,2007,43(5):210-213.
[9]王连东,张伟,程嘉,等.普通液压机超高压液压胀形集成装置的研制[J].中国机械工程,2007,18(21):2624-2627.

