箱型支撑结构加筋板布局设计方法研究

丁晓红 李国杰

1.上海理工大学，上海，200093 2.三一集团港机公司上海研究院，上海，201200

0 引言

箱型支撑结构一般由外壁及布置于内部的纵横加筋板组成，纵横布置的内部加筋板可增加箱型支撑结构的强度和刚度，使箱型结构具有轻质、高强度、高刚度的优点，因此在工程实际中得到了日益广泛的应用，如机床的床身、立柱等支撑件，起重机的大梁与支腿，以及船舶船体、车辆车体结构等。箱型支撑结构内部加筋板的布局是影响结构力学性能的主要因素，因此如何在箱型支撑结构内部合理地布置加筋板，使结构的机械性能达到最优是一个值得研究的问题。目前，大多数箱型支撑结构加筋板优化设计问题都局限于加筋板间隔与截面的尺寸优化设计［1－4］，而加筋板的形式及布局优化设计自由度大，实现困难，研究成果较少。由材料力学理论可知，对箱型结构来说，纵向加筋板抗弯效果好，设置于弯曲平面内；横向加筋板抗扭作用大，在垂直于扭矩的矢量方向上设置；斜向加筋板具有同时提高抗弯、抗扭的综合效果。目前大部分箱型支撑结构内部加筋板布局均从上述理论出发，根据经验提出各种加筋板的形式，如垂直对角筋、垂直纵向筋、垂直横向筋、空间对角筋，在对这些加筋结构进行力学分析比较的基础上，对原有设计进行改进［5－7］，或者在确定了若干个加筋板布局形式的基础上进行布局选型及尺寸优化设计［8］。近年来，随着结构拓扑优化设计理论的发展，加强筋的布局优化问题得到了深入的研究，尤其是薄壁板壳结构加强筋的分布优化设计［9－11］。对于箱型结构来说，将箱型结构内部填充材料，然后对其内部的实体采用结构拓扑优化设计方法进行设计，可得到内部加筋板的优化布局［12］。但对于工程中常见的大体积箱型支撑结构，采用拓扑优化设计方法计算量相当大，且其设计结果形态复杂，实际应用中还需要进行进一步的后处理，因此虽然从理论上说该方法行之有效，但实际应用还相当少。

本文针对箱型支撑结构内部加筋板的设计问题，采用简化的纤维模型，提出了一种基于密度法的高效设计方法。首先将箱型结构表示为内部布置有平行分布杆的结构，即建立相应的纤维模型，通过对承载外壁的材料分布进行优化设计，确定内部杆存在与否，将存在的杆连接起来形成箱型结构的内部加筋板。通过对悬臂箱型结构、具有曲面的底部支撑箱型结构和机床床身箱体的典型设计实例的分析，说明本方法的有效性。

1 设计方法

1.1 设计模型的简化

由外壁和加筋板组成的箱型结构可简化为纤维模型：加筋板可看成由平行的纤维组成，这些纤维一端连接着承载的外壁，另一端连接着结构的支撑面，如图1所示。其中，图1a表示具有对角筋板的箱型结构，将筋板看成由图1b所示的平行纤维组成。将平行纤维表示为有限元模型中的梁单元，则可得到图2所示的具有内部平行梁单元的箱型结构的初始有限元设计模型，即纤维模型，其中与梁单元相连的承载面和支撑面均划分为相同的壳单元。

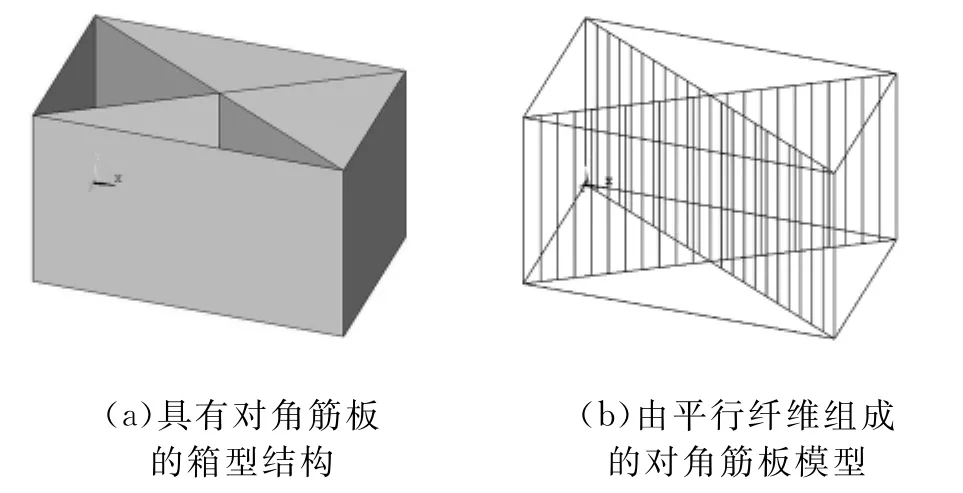
图1 对角筋板的纤维模型表示

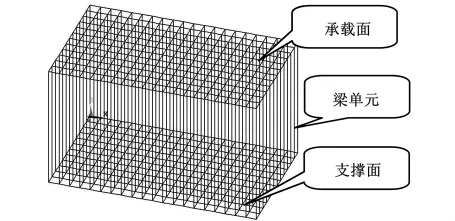
图2 具有内部平行梁单元的箱型结构初始有限元设计模型

1.2 基于密度法的外壁材料分布优化

将箱型支撑结构简化为纤维模型后，以承载外壁作为设计区域，通过设计外壁的材料优化分布，确定内部平行梁单元的布局，即保留与外壁存在材料区域相对应的梁，去掉与外壁删除材料区域相对应的梁，并将保留的梁连接起来，即构成内部的加筋板。这样就将原来复杂的三维实体结构的拓扑优化设计问题转化为二维板壳结构的拓扑优化设计问题。

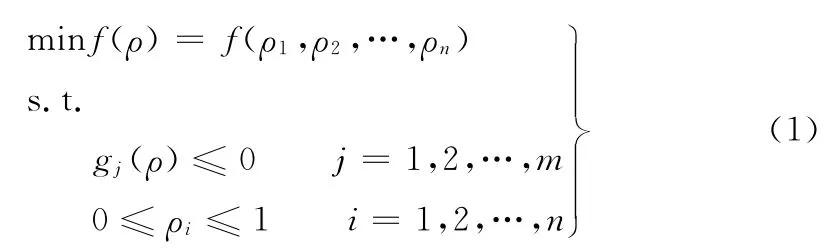
板壳结构的拓扑优化设计方法比较成熟，本文采用密度法［13］进行设计。所谓密度法就是将材料的密度作为设计变量，密度从0到1连续变化，1表示有材料，0表示没有材料，密度在0～1之间的材料为虚拟材料，称为中间密度材料。则优化设计问题可描述为

式中，ρi为单元i材料的密度；n为单元数；m为约束条件数。

为了消除中间密度材料，使设计结果仅存在密度为0和1的材料，单元刚度矩阵计算时采用下式对中间密度进行“惩罚”：

式中，K′为惩罚后的单元刚度矩阵；ρ为单元的材料密度；K为实际的单元刚度矩阵；p为惩罚因子，通常p的取值在2～3之间［13］。

以结构体积最小为设计目标，并满足结构的变形及应力约束，基于密度法的外壁材料分布优化设计问题可描述为

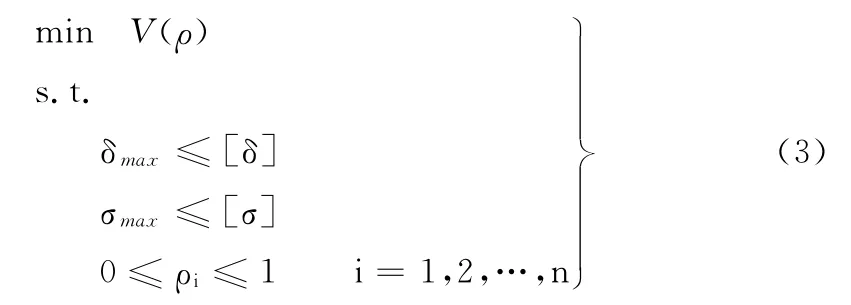
式中，V为结构的总体积；δmax、σmax分别为结构的最大位移和最大应力；［δ］、［σ］分别为结构的许用位移和许用应力。

综上所述，具体的设计流程为：首先将设计对象简化为中空的箱体，对其进行有限元网格划分，注意箱体的约束面和设计面的网格需一一对应；在上下对应的节点上建立与设计面垂直的梁单元，即构建纤维模型。施加载荷和约束，进行静力分析。然后应用密度法，根据式（3）对设计面进行材料的最优分布设计。最后根据设计面的材料分布优化设计结果，确定应保留的梁单元，连接各梁单元形成加筋板。

2 典型算例

2.1 悬臂箱型梁加筋板布局优化设计

为了验证本文方法的有效性，首先以简单的悬臂梁承受扭转载荷情况为例进行讨论。悬臂箱型梁模型如图3a所示，梁的长高比为2，截面为正方形，梁的自由端作用载荷，使梁受扭。图3b所示为相应的有限元模型，中空的箱型梁内部布置水平的梁单元，以连接固定端和自由端。将自由端面作为设计面，以结构体积最小为设计目标，满足结构的刚度和强度要求，应用密度法对其进行拓扑优化设计，得到的设计结果如图3c所示。

由图3c可知，受扭悬臂箱型梁的加筋板应布置为对角筋板的形式，这样的形式可由材料力学中关于梁的理论得到合理的解释：由于受到纯扭转，各点的应力状况为纯剪切，在45°的对角方向上存在主应力，因此对角布置的加筋板近似受拉或受压，受力状况良好。由此可认为，应用本文方法进行箱型梁加筋板布局优化设计是合理的。

为了说明结构的合理性，以结构的总应变能与体积的乘积作为结构综合性能指标μ，即

式中，E为结构的弹性应变能，其值越大，说明结构的柔度越大，刚度越小。

考虑刚度最优的理想结构是结构的体积最小而应变能也最小，即性能指标μ的值越小越好。

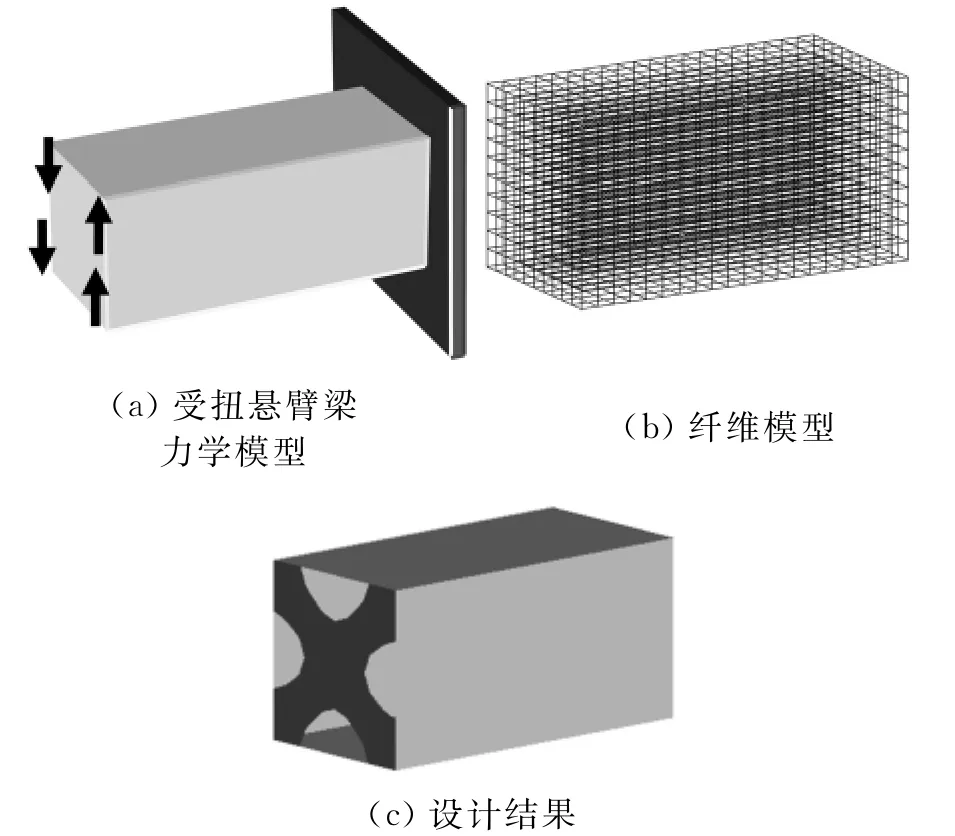
图3 受扭悬臂梁的设计

将图3c所示具有对角加筋板的悬臂箱型梁结构和内部没有加筋板而具有与图3c相同外形几何尺寸的梁进行比较。设计模型和加载情况如图4所示，表1列出了两种悬臂梁模型的总应变能、最大应力、最大变形、体积及性能指标μ，表1中将中空悬臂梁的各项指标表示为1。可见，具有对角加筋板的结构体积是中空梁的1.63倍，而性能指标仅为前者的0.26倍，相应地，加筋结构的总应变能、最大应力和最大变形分别为中空结构的0.16倍、0.27倍、0.15倍，说明布置有对角加筋板梁结构的力学性能大幅度提高，抗扭刚度可提高6倍以上，而其综合性能指标也提高了近4倍，进一步说明了由本文方法设计得到的对角加筋板的箱型悬臂梁的合理性。

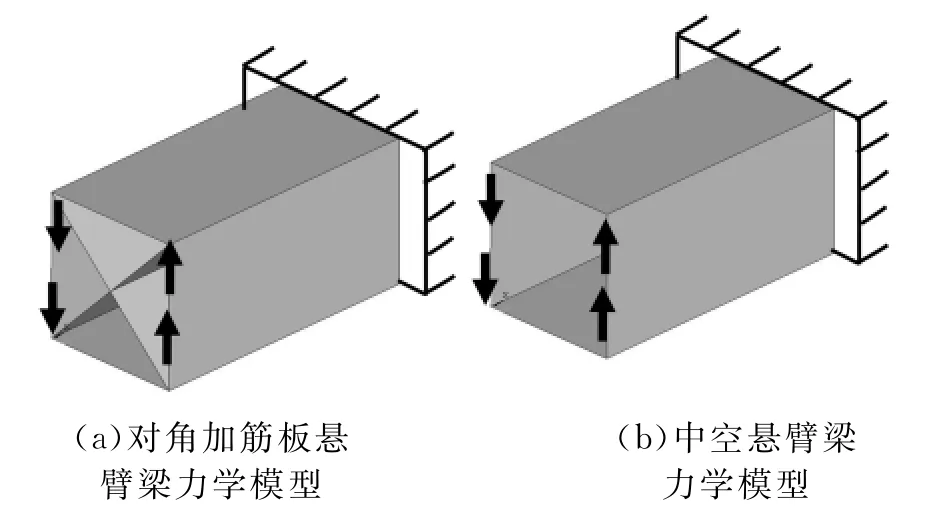
图4 悬臂梁的力学模型

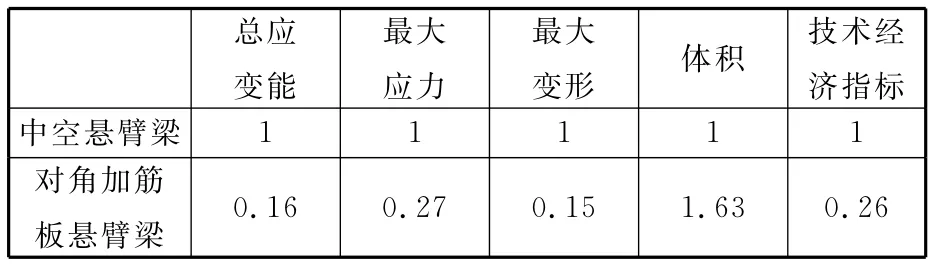
表1 悬臂梁性能对比

2.2 曲面箱型支撑结构

为了进一步说明本文方法的有效性，以形状较复杂的曲面箱型支撑结构为例，考察不同的形状几何参数对加筋板布局结果的影响。图5a所示为设计模型，结构的横截面为矩形，侧面为曲面壁板围成，结构底部支撑，上面承受扭转载荷。曲面壁板长度与矩形横截面高度之比为3.3，矩形横截面的高度h与宽度w之比为ζ，即ζ＝w／h。

图5b为相应的纤维模型，中空的箱型梁内部布置竖直的梁单元，以连接承载面和支撑面。图5c～图5e所示为当形状几何参数ζ分别为1.0、1.5和2.0时的加筋板布局设计结果。由图5可知，随着形状几何参数ζ的变化，箱型结构内部加筋板的布局也发生变化：当ζ＝1.0时，仅在4个角上出现对角的加筋板，结构中部由于横向较窄，抗扭刚度较大，不需要布置加筋板；当ζ＝1.5时，结构中部出现斜向加筋板，将两端的加筋板连在一起，以增大结构的抗扭刚度；而当ζ＝2.0时，中部加筋板变厚，两端的加筋板尺寸变小。显然，形状几何参数ζ的增大导致箱型结构内部空间增大，抗扭刚度减小，需在结构内部合理地布置加筋板，以提高结构整体刚度。

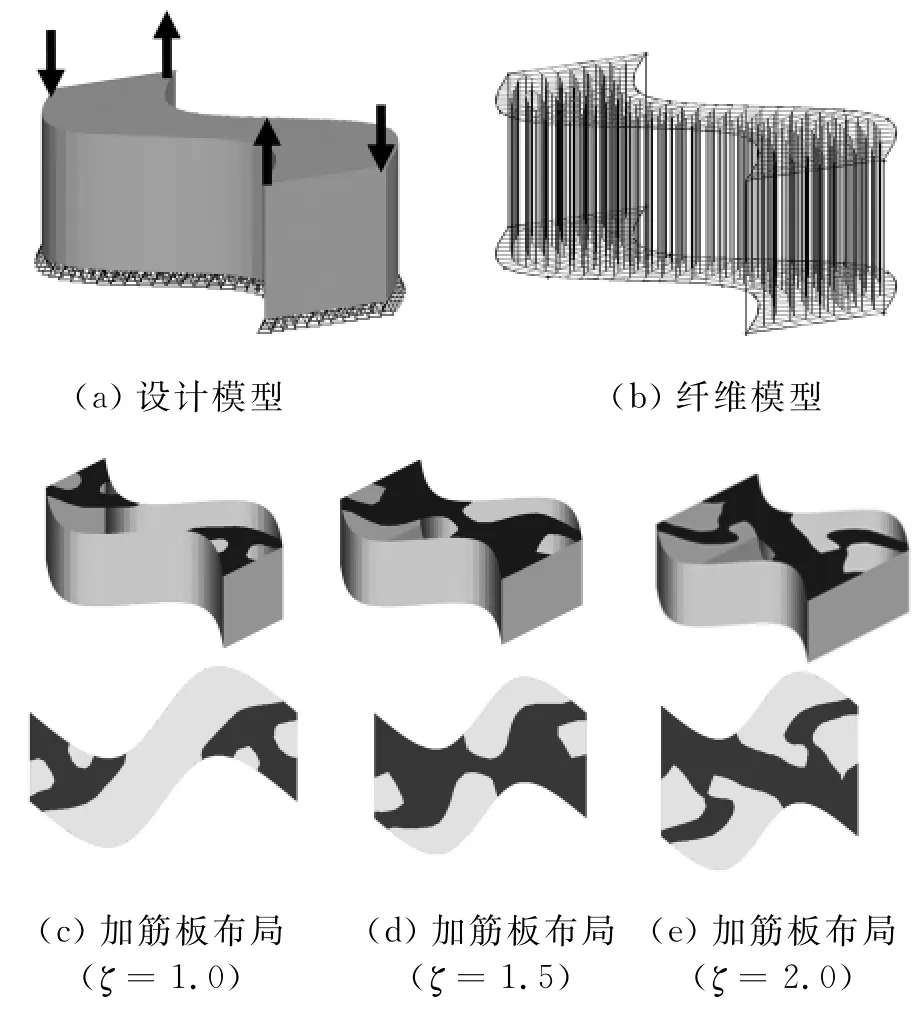
图5 曲面箱型支撑结构加筋板布局设计

2.3 机床床身结构内部加筋板布局优化设计

机床床身起着支撑和连接工作台、头尾架等关键零部件的作用，其刚度与整机加工精度密切相关。同时，在整个机床的各个组成部分中，床身的重量大约占机床总重量的20%以上，其材料用量和制造工艺费用对整机的经济性能有很大的影响。因此，对床身结构进行优化设计，得到刚度大、重量轻的结构对提高机床整机的性价比十分必要。机床床身承受的载荷比较复杂，包括其上支撑的工作台、工件等部件重量，切削力及其本身自重等，这些载荷不仅使床身受压，同时使床身受扭及斜弯曲。试验表明，在各种变形中，扭转变形可占总变形的60%以上［6］，因此本文主要研究如何在床身结构内部布置合理的加筋板，以提高床身的抗扭刚度。

受扭床身的力学模型如图6所示，图6a为床身头尾架上承受绕x轴的扭矩静力当量载荷时的情况，图6b为相应的力学模型。本文设计的床身外形尺寸为2700mm×1170mm×700mm，截面为长方形，壁厚为15mm。根据本文提出的设计方法，床身的纤维模型如图6c所示。将床身底面固定，以上表面为设计面，根据式（3）的优化模型，以体积最小为设计目标，考虑结构的变形和应力约束，得到设计面的材料分布如图6d所示。由图6可知，为了提高床身箱体的抗扭刚度，两组对称的对角加筋板由一位于床身中心轴线上的纵向加筋板连接在一起，形成床身箱体的内部加筋板结构。

图7a所示为床身承受的另一种典型的载荷情况，此时床身头尾架上承受沿y轴的静力当量载荷。将该静力当量载荷简化到床身上，如图7b所示，此时床身承受扭转和剪切的组合载荷作用。图7c为相应的纤维模型，采用和图6相同的设计过程，设计面的材料分布如图7d所示。和图6d相比，同样需要在床身两端布置两组对称的对角加筋板以提高结构的抗扭刚度，但在结构中部会出现米字形的横向加筋板结构。

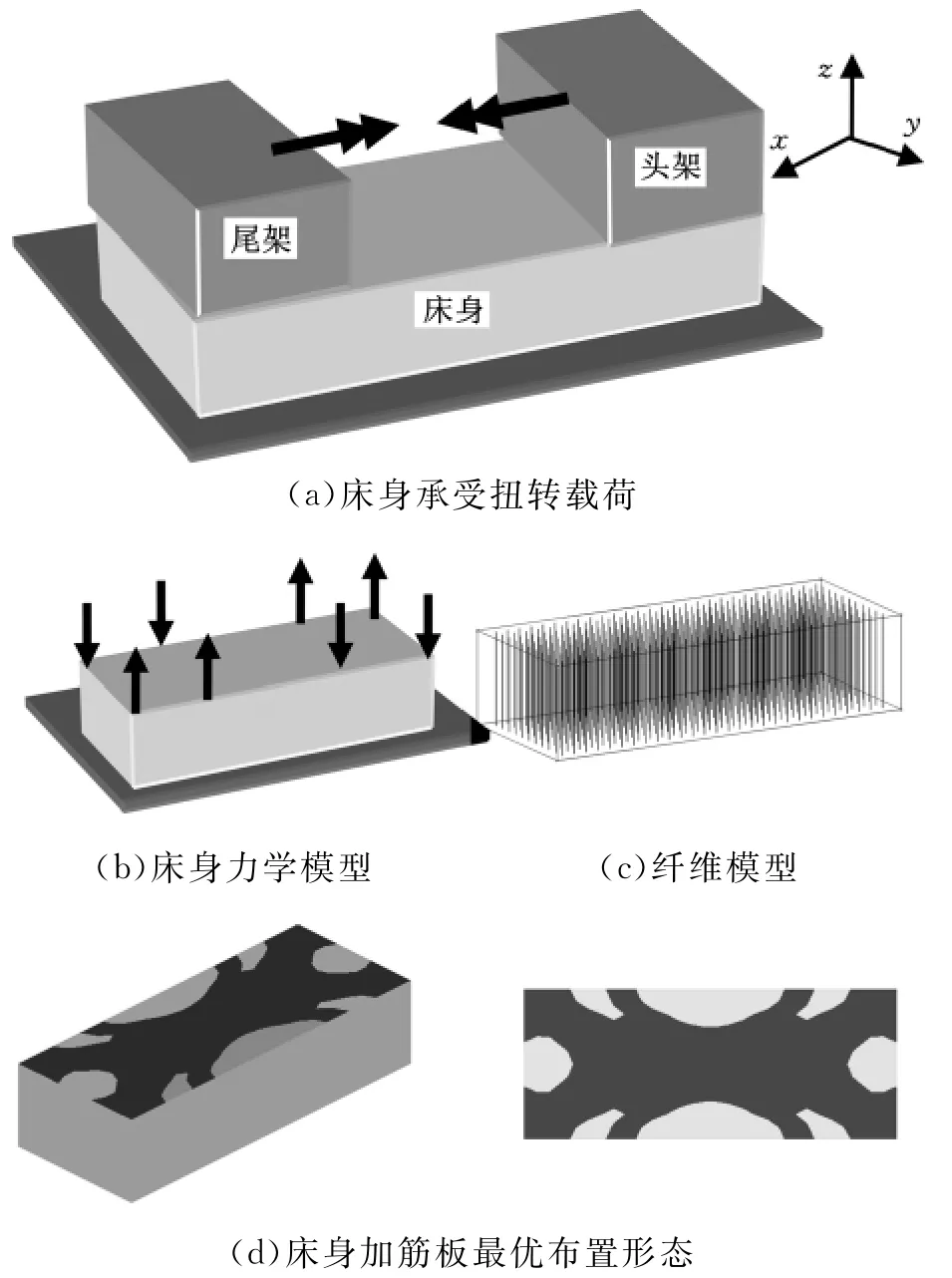
图6 受扭床身加筋板设计

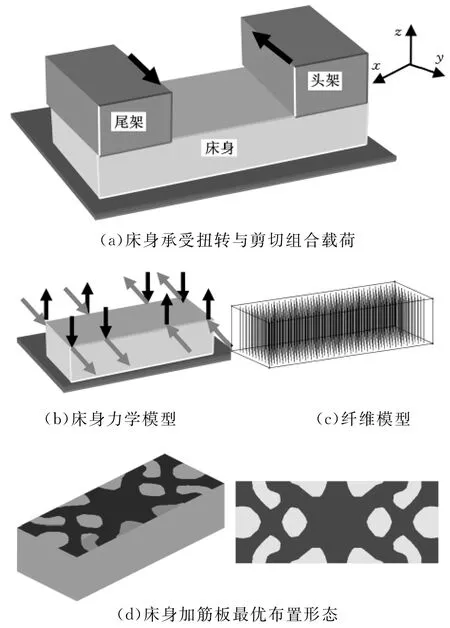
图7 受扭剪组合载荷床身加筋板设计

根据图6d和图7d所得的设计结果，分别建立图8a和图8b所示的带有加筋板的箱体结构。为了说明设计结果的合理性，将图8a和图8b所示的优化设计模型与图8c所示的目前常见的带横隔板的床身结构进行比较。三种床身箱体在纯扭转载荷和扭转剪切组合载荷作用下的力学性能和性能指标列于表2，表2中将带有横隔板的床身结构的各项指标表示为1。由表2可见，纯扭转优化设计模型的体积最小，是横隔板模型的0.983倍；而组合载荷优化设计模型的体积最大，是横隔板模型的1.02倍。在纯扭转载荷作用下，纯扭转优化设计模型的性能指标μ最小，比横隔板模型减小26.7%，应变能比横隔板模型减小25.5%，体积减小1.7%，因此最优；而在扭转和剪切组合载荷作用下，组合载荷优化设计模型的性能指标μ比横隔板模型减小9.5%，应变能比横隔板模型减小11.3%，体积增大2.0%，因此最优。可见采用本文提出的设计方法可有效布置床身内部的加筋板，提高床身结构的技术经济性能。

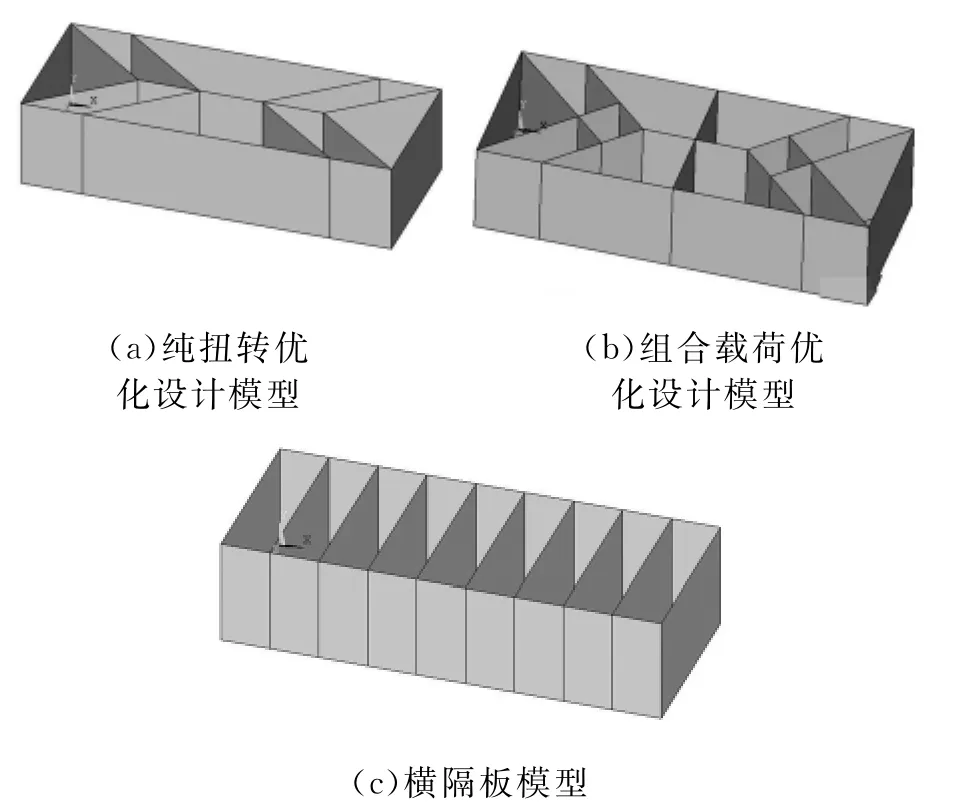
图8 各种加筋板的床身模型

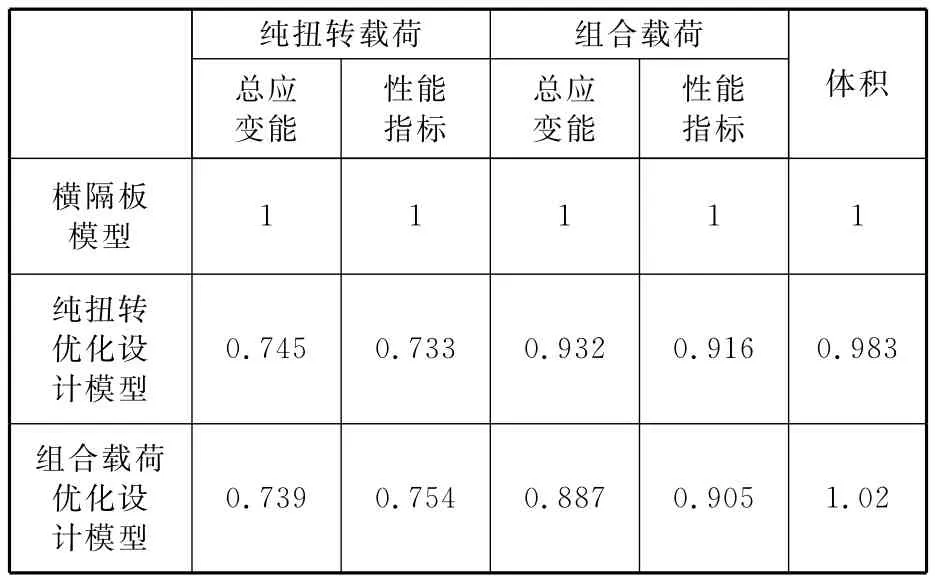
表2 各种加筋板的床身性能对比

3 结语

本文采用合理的纤维模型，将三维实体拓扑优化设计问题转化为二维板壳结构的拓扑优化设计问题，提出了一种高效的箱型支撑结构内部加筋板优化布局设计方法，以若干典型实例验证了所提出方法的有效性。本方法可广泛应用于各种支撑箱型结构的加筋板布局优化设计中。

［1]朴春雨，章怡宁.典型加筋板的优化设计［J］.飞机设计，2003（4）：29－32.

［2]马歆，郑津洋，陈西南，等.内压载荷下复杂薄壁箱型结构数值模拟与优化设计［J］.浙江大学学报（工学版），2006，40（5）：898－902.

［3]Ryu Y，Kim J，Cho H，et al.LRFD－based Design Optimization of Steel Box Girder Sections Using Genetic Algorithms［J］.Structural Engineer，2002，6（2）：127－134.

［4]J′armai K，Farkas J.Optimum Cost Design of Welded Box Beams with Iongitudinal Stiffeners Using Advanced Backtrack Method［J］.Structural Multidisciplinary Optimization，2001，21（1）：52－59.

［5]刘晓波.机车车体结构加强筋的合理设计［J］.机车电传动，2008（1）：42－44.

［6]叶瑞汶.机床大件焊接结构设计［M］.北京：机械工业出版社，1986：128－163.

［7]杨晓京，傅中裕，刘剑雄.基于ANSYS的XK640数控铣床立柱优化设计［J］.机械设计与制造，2006，（11）：73－74.

［8]张柱国，姚卫星，刘克龙.基于进化Kriging模型的金属加筋板结构布局优化方法［J］.南京航空航天大学学报，2008，40（4）：497－500.

［9]Ding X，Yamazaki K.Growth Technique of Stiffener Layout Pattern for Plate and Shell Structures to A－chieve Minimum Compliance［J］.Engineering Optimization，2005，37（3）：259－276.

［10]Lam Y C，Santhikumar S.Automated Rib Location and Optimization for Plate Structures［J］.Structural Multidisciplinary Optimization，2003，25（1）：35－45.［11]Luo J，Gea H C.A Systematic Topology Optimization Approach for Optimum Stiffener Design.Structural Optimization，1998，16（4）：280－288.

［12]Chang C，Zheng B，Gea H.Automated Design of Thin－walled Packaging Structures［J］.Structural Multidisciplinary Optimization，2008，35（6）：601－608.

［13]Bruns T.A Reevaluation of the SIMP Method with Filtering and an Alternative Formulation for Solidvoid Topology Optimization［J］.Structural Multidisciplinary Optimization，2005，30（6）：428－436.