基于挠度分析变截面箱型梁的剪力滞效应
韩 娇 尹锡锡 王 展 韦春宜 周月娥
(广西民族大学建筑工程学院,广西 南宁 530006)
0 引言
箱型梁因其良好的力学性能而被运用于各类工程中,箱型梁由顶板、底板、腹板和翼缘板组成。等截面箱梁得到了比较多的研究和应用,变截面箱梁因具有较好的灵活性,即在弯矩不同处可选择不同截面大小,也得到了广泛运用。文献[1]针对等截面连续箱梁,提出了一种当量截面法,将理论计算结果与实验结果进行了分析比较。文献[2]针对大挠度问题,建立势能泛函,用有限元的方法求解变截面箱梁的剪力滞效应。文献[3]在考虑剪力滞的同时考虑剪切变形效应,采用两种不同的方法建立了变截面箱梁的挠度和剪力滞系数的求解公式。文献[4]针对连续箱梁,利用有限梁段法建立了剪力滞系数求解公式。文献[5]利用正弦函数建立箱梁的纵向位移函数,用有限差分法建立了求解剪力滞系数和应力的公式。文献[6]利用变分法和有限梁段法分析了变截面箱梁的剪力滞效应。
本文基于箱型梁剪力滞效应分析的能量变分法[7],结合变截面箱型梁剪力滞效应分析的当量截面法建立了基于附加挠度的变截面箱梁解析分析方法。并在此基础上,推导了悬臂和简支箱型梁受均布荷载作用下挠度、剪力滞系数和应力的计算公式。
1 等截面箱型梁的控制微分方程
基于附加挠度的箱型梁控制微分方程[7]:

式中:参数I、n 和k 的定义及取值表达式可参阅文献[7]。
2 剪力滞效应的影响因素及当量值
由式(2)可知,在q 一定的情况下,附加挠度wa(x)随参数I、n 和k 变化。参数n 值是Is/I 的函数,参数k 值是Is/I 和Is/I 的函数,有关Is和Is的定义及取值表达式可参阅文献[7]。
当箱型梁截面是变化的,其翼板的刚度和箱梁的总刚度也是变化的,即Is和Is是x 的函数:

根据上面I、Is/I 和Is/与x 的关系,参照等截面箱型梁的方法推导附加挠度的控制微分方程是很困难的。为了能利用分析等截面箱梁的方法,从近似计算角度出发,将箱梁沿跨长分段,在各个分段上计算I、Is和Is/。按式(6)求出三个当量值m1、m2和m3作为当量等截面梁的I、Is/I、和Is/代替原来的变截面梁,达到简化求解变截面梁的目的。当量值m1、m2和m3用下式计算:

3 变截面箱型梁的控制微分方程
针对均布荷载作用下的箱型梁,将当量值m1、m2和m3代入式(1)和(2)得变截面箱型梁的控制微分方程为:

式中,
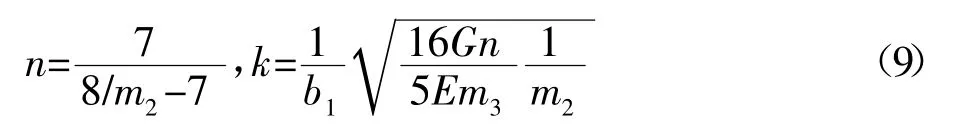
边界条件与文献[7]讲到的边界条件是一样的,只是涉及参数k 和n 时,取式(9)的表达式进行计算。
4 变截面箱型梁附加挠度解析解
式(7)定义的四阶常微分方程是w″a的二阶常微分方程,其通解为:

对上式求一次、二次积分和一阶导数,可得:


上式中的待定系数可利用边界条件求出。
5 悬臂箱型梁的剪力滞系数
5.1 悬臂箱型梁受均布荷载作用下的挠度
当箱型梁为左端固定右端自由时,其边界条件是:

结合式(10)~(13),联立求解方程组可得式(12)中的待定系数:

继而可得悬臂箱型梁的附加挠度:
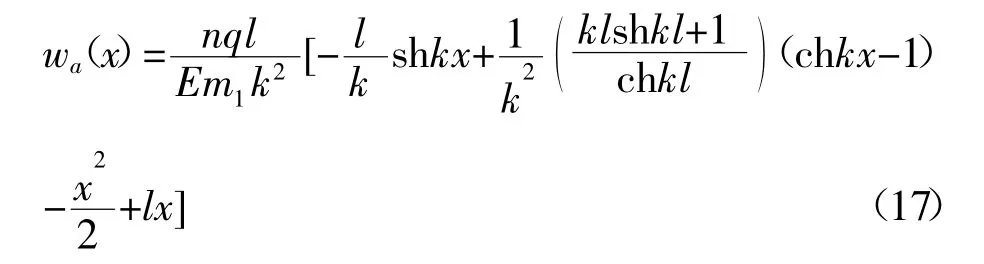
求出箱梁截面的弯矩M(x)=-q(l-x)2/2,再根据关系式EIw‴c=-M(x)通过积分可得:

箱型梁wc(x)的边界条件满足:

结合式(18)进行两次积分确定:B1=B2=0,得wc(x)的表达式:
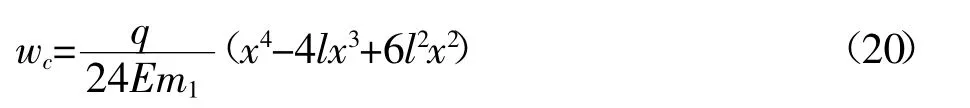
5.2 悬臂箱型梁的剪力滞系数
悬臂箱型梁的剪力滞系数表达式:
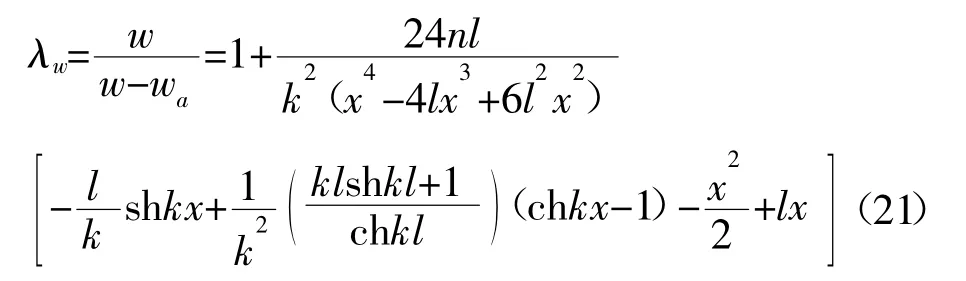
左端点处的剪力滞系数:

6 简支箱型梁的剪力滞系数
6.1 简支箱型梁受均布荷载作用下的挠度
当箱型梁左右端均为简支时,其边界条件是:

结合式(10)~(12),联立求解方程组可得式(12)中的待定系数:

继而可得简支箱型梁的附加挠度:

根据初等梁理论可求得箱梁截面的弯矩M(x)=qx(l-x)/2,进而根据挠度wc(x)与截面弯矩M(x)的关系式通过积分可得:

箱型梁wc(x)的边界条件满足:

结合式(26)进行两次积分确定:B2=0,B1=ql3/24,得wc(x)的表达式:

6.2 简支箱型梁的剪力滞系数
简支箱型梁的剪力滞系数表达式:

左右端点处的剪力滞系数:

7 箱型梁受均布荷载作用下应力
当箱型梁的边界条件为左端固定、两端简支或是两端固定,将前面得到的不同边界条件下的w″a和w″c代入下式,就可以计算翼缘横截面上的正应力:

8 结语
本文结合基于附加挠度的能量变分法和变截面箱型梁分析的当量截面法建立了适合变截面箱型梁剪力滞效应分析的解析方法。结合悬臂和简支箱型梁在均布荷载作用下的边界条件推导了箱型梁挠度、剪力滞系数和应力的解析计算公式,为变截面箱型梁剪力滞效应分析提供了一种新的解题思路。

