圆柱斜齿轮浮动凹模冷挤压成形仿真与实验研究

薛克敏 李晓冬 李 萍 许 锋 周结魁 石文超

合肥工业大学，合肥，230009

0 引言

与直齿轮相比，圆柱斜齿轮具有轮齿重合度高，传动平稳，冲击、振动小等优点，在机械传动领域有着广泛的应用。目前对斜齿轮的成形主要采用切削加工，这不仅破坏了金属的流线性分布，更导致加工后的斜齿轮抗弯、抗疲劳强度大打折扣。对齿轮采取近净成形工艺，就是通过精密挤压技术来达到齿廓不需或仅需少许精加工的方法。通过该方法获得的齿轮锻件，由于金属受三向压应力，其内部疏松、微裂纹等缺陷得以锻合，工艺塑性得以改善，且金属纤维沿齿形均匀分布，齿轮的使用寿命显著提高［1－3］。

然而，圆柱斜齿轮形状较为复杂且存在一定的螺旋角，当采用挤压工艺成形时，成形后的齿轮锻件如何从凹模型腔中顺利脱模，成为制约圆柱斜齿轮近净成形研究的瓶颈。目前国内外学者对圆柱斜齿轮近净成形工艺进行了研究。Choi等［4］通过上限法分析了斜齿轮导向式和闭式两种锻造工艺，并进行了相关的实验验证；吴昊等［5］采用闭式温锻的工艺模拟了圆柱斜齿轮的成形过程。本文针对某一型号两种螺旋角的圆柱斜齿轮，采用浮动凹模的工艺进行冷挤压成形和脱模的研究，探索了在这两个过程中，影响其成形效果和脱模后斜齿轮精度的因素。

1 圆柱斜齿轮浮动凹模成形工艺分析

和圆柱直齿轮相似，斜齿轮在冷挤压成形时，也存在成形力过大、齿形角隅部分难充填等困难。采用浮动凹模结构，可有效改善摩擦条件，改善坯料在模具型腔的充填情况，降低成形载荷，减少模具的磨损等。

当采用传统的闭式挤压成形时，下冲头及凹模固定，上冲头以速度v向下运动，如图1a所示。毛坯的主要流动方向是朝下的，凹模相对于毛坯向上运动，毛坯在挤压过程中受到凹模施加的摩擦力作用，该摩擦力方向与金属运动方向相反，随着挤压过程的进行，摩擦力会越来越大，最后导致斜齿轮的上下角隅处难以充填。若将凹模改为可浮动的，如图1b所示，在挤压变形开始时，凹模在上冲头的压力下，随其以同一速度v下行。整个变形过程中，凹模对坯料产生摩擦力，但该力方向沿轴向向下，与金属运动方向相同，最终可促进齿形角隅部分的充填［6］。

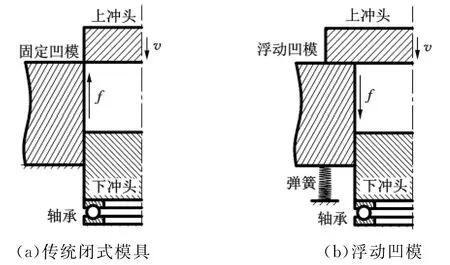
图1 模具工装对比图

由于圆柱斜齿轮存在一定的螺旋角，在挤压成形和脱模时，下冲头会在凹模齿腔的导向作用下，自动地沿着螺旋角方向边旋转边沿轴向向上运动，为方便下冲头运动，可在其底部安装推力球轴承。

2 工艺过程有限元模拟

为了进一步探索圆柱斜齿轮在浮动凹模冷挤压成形过程中金属流动规律以及影响脱模后齿轮精度的因素，本文以某一型号的两种圆柱斜齿轮为对象进行了相关研究。斜齿轮的基本几何参数如下：齿数为22，法面模数为2.5mm，压力角为20°，齿顶高系数为1.0，顶隙系数为0.25，螺旋角分别为22°和32°。

2.1 有限元模型的建立

运用Deform－3D有限元软件，采用刚塑性有限元法，对圆柱斜齿轮浮动凹模冷挤压成形过程进行计算机仿真模拟。模拟时坯料所选材料为20CrMnTi，将模具视为刚体，不发生弹塑性变形，坯料和模具的初始温度均设定为室温25℃。为精确建模及节省计算时间，划分网格时，对圆柱斜齿轮的齿形部分进行局部细化，网格总数为1.2×105，齿形与其余部分网格尺寸比为1∶10，建立的有限元模型如图2所示［6］。

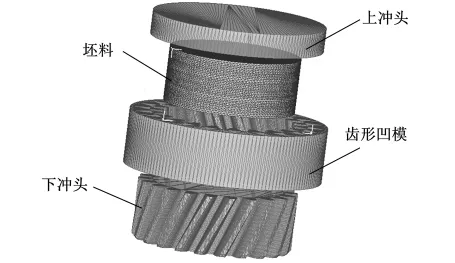
图2 斜齿轮模具与坯料的有限元模型

2.2 摩擦模型的建立

在进行有限元模拟及物理实验时，需正确处理毛坯金属与模具之间的摩擦关系［7］。不考虑接触面上的黏合现象，本文采用应用比较广泛的库伦摩擦模型，其数学表达式为

式中，f为与速度方向相反的摩擦力；μ为摩擦因数；Pn为法向压力。

3 浮动凹模成形过程模拟与实验

3.1 实验过程

为了降低实验成本，简化实验过程，本次实验毛坯材料选用工业纯铅。分别制作了螺旋角为22°和32°的两套简易模具来作工艺对比。在挤压成形时为便于斜齿轮下冲头自由地在齿形凹模内沿轴向和圆周方向运动，在设计模具时，下冲头齿顶圆直径较标准齿形小0.05mm，如图3所示［8－9］。成形设备是2MN 液压机。

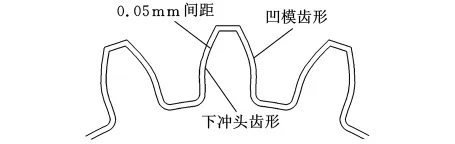
图3 下冲头齿形示意图

3.2 模拟与实验结果分析

表1所示为采用传统闭式挤压工艺和浮动凹模冷挤压工艺时，螺旋角分别为22°和32°的圆柱斜齿轮不同压下量的成形效果对比图。现以前者为例进行成形分析。从表1中第1组图可以看出，若采用传统的闭式挤压工艺成形圆柱斜齿轮，由于上下冲头与坯料表面的摩擦作用，毛坯在挤压过程中表现出中部径向流动速度快，上下端部流动较慢的特征。当压下量达到30%时，锻件中部出现一定量的鼓形趋势，但不明显；当压下量达到60%时，形成鼓形的趋势加剧，上下端部径向流动明显滞后，因此在后续成形过程中，主要完成上下端部及其角隅部分的充填。若对其采用浮动凹模工艺成形（如表1中第2、第3组图所示），由于浮动凹模改变了摩擦力的方向，使其与金属的流向相同，从而加快了毛坯的中下部金属的径向充填速度。当压下量达到30%时，已出现上端径向流动滞后于下端，锻件略微呈现梯形；当压下量达到60%时，形成梯形的趋势明显加剧，锻件下端及中部齿形已经充填大部分，此时上端齿形刚开始充填，因此在后续成形过程中，主要完成上端部齿形及其角隅部分的充填。

对于螺旋角为32°的圆柱斜齿轮，在浮动凹模冷挤压工艺下（如表1中第4、第5组所示），其成形规律与螺旋角为22°时相似。

图4所示为两种斜齿轮在传统闭式挤压工艺和浮动凹模冷挤压工艺下成形载荷随时间增量步变化曲线。圆柱斜齿轮采用浮动凹模冷挤压工艺时，整个冷挤压过程所需的成形力相对于传统闭式挤压工艺明显降低。螺旋角为22°和32°的圆柱斜齿轮采用浮动凹模冷挤压工艺成形时载荷分别为6.0MN和7.1MN，而采用传统闭式挤压工艺时两者的成形载荷分别为8.5MN和9.5MN。相比之下，采用浮动凹模工艺成形时工作载荷可分别降低约30%和25%。

注：第1组为22°螺旋角传统工艺等效应变图；第2组为22°螺旋角浮动凹模成形等效应变图；第3组为22°螺旋角浮动凹模成形实验效果图；第4组为32°螺旋角浮动凹模成形等效应变图；第5组为32°螺旋角浮动凹模成形实验效果图。

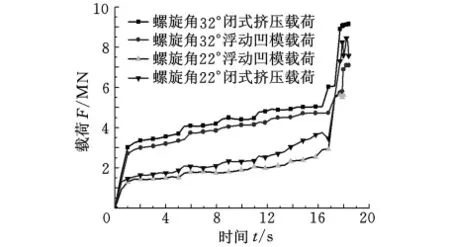
图4 成形载荷－时间曲线图

4 脱模过程模拟与实验分析

圆柱斜齿轮在脱模时若工艺参数控制不当，势必会使成形好的锻件产生破坏性的变形，导致其无法修复。而影响脱模过程的因素较多，其中比较显著的有摩擦因数和螺旋角。脱模时，单个齿形的受力情况如图5所示。

图5中，F为下冲头施加的脱模力，方向竖直向上；F1、F2分别为F沿着齿形方向和垂直于齿形方向的分力；β为斜齿轮螺旋角；Fz为齿形在挤压成形时，由于胀形而对凹模产生的作用力，该力的方向应垂直于齿形，对于既定的工艺，Fz可取常数（其值近似等于当β＝0，μ＝1而其他参数不变时的脱模力，通过数值模拟，浮动凹模成形工艺下Fz约为182.61kN）。

假设在脱模时，斜齿轮锻件能匀速被顶出，则有下列受力平衡关系：

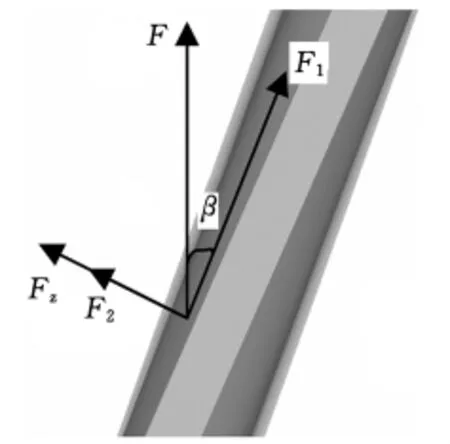
图5 单个齿形受力图

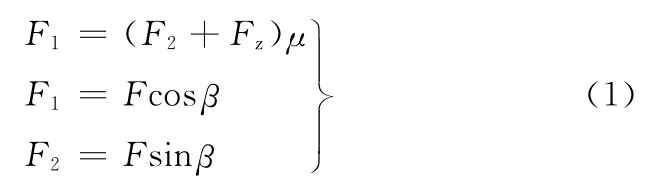
式中，F、β、μ为变量；Fz为常数。

4.1 摩擦因数对脱模过程的影响

当螺旋角β一定时，由式（1）可得F与μ有下列关系式：

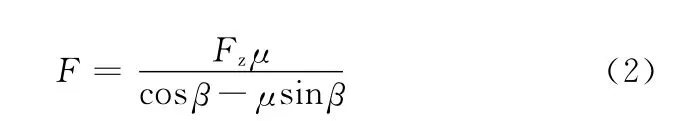
当摩擦因数μ分别取0.10、0.12、0.14时，通过式（2）计算可得表2。

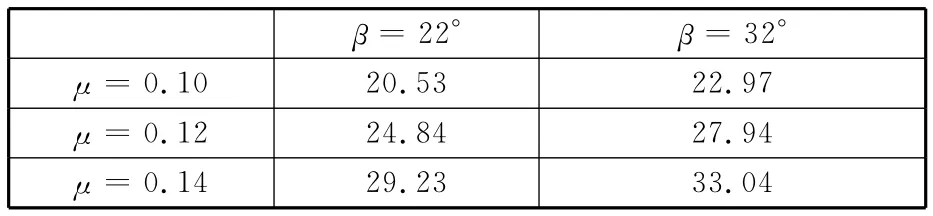
表2 脱模力理论计算表 kN

从表2可以看出，当螺旋角β不变时，脱模力随摩擦因数μ的增大而增大。图6为在三种摩擦因数下，圆柱斜齿轮通过数值模拟所获得的脱模力随时间变化曲线图，由模拟曲线可以看出，当μ分别取0.10、0.12、0.14时，螺旋角为22°的圆柱斜齿轮脱模力分别在20kN、24kN、29kN上下波动；螺旋角为32°时，其波动值则分别为22kN、27kN、33kN。由此可见，数值模拟与计算结果是较为吻合的，在一定程度上验证了数值模拟的可靠性。

4.2 螺旋角对脱模过程的影响

当摩擦因数μ一定时，由式（1）可得F与β有下列关系式：

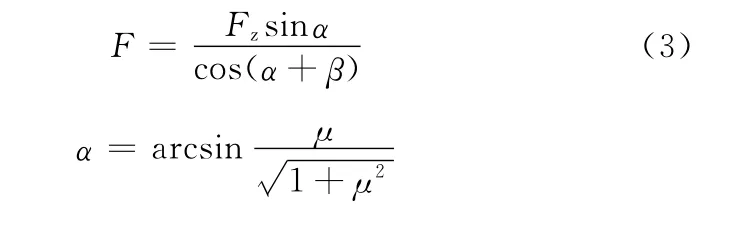
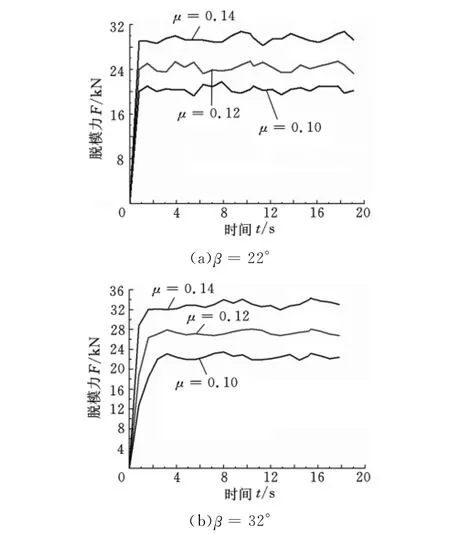
图6 脱模力－时间变化曲线图

图7为摩擦因数μ＝0.10时，脱模力F与螺旋角β之间的关系曲线图。从图7可以看出，脱模力随着螺旋角的增大而增大，且增大的趋势越来越快。当β＝22°和32°时，脱模力分别达到约20kN和23kN。

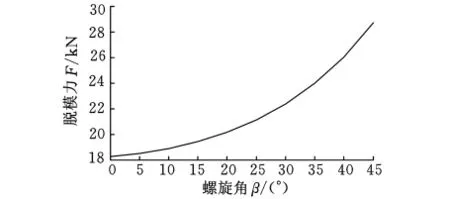
图7 μ＝0.10时，F与β曲线图

4.3 模拟与实验结果对比

表3所示为斜齿轮锻件脱模过程中模拟与实验结果对比分析。从速度场可以看出，齿轮锻件在脱模时，金属的流动速度均沿着齿形方向，且大小相近，这说明在脱模过程中，齿形在凹模的导向作用下，自动地沿着螺旋方向做刚性旋转运动，几乎不产生塑性变形，可有效地保证脱模后斜齿轮锻件的精度。从应变场可以看出，螺旋角为22°的斜齿轮锻件脱模后，等效应变主要集中在上下齿形的角隅部分，其余部分几乎没有变形；当螺旋角增大到32°时，等效应变除了集中在齿形角隅部分外，中部齿形也出现微小的应变。因此，随着螺旋角的增大，脱模后的斜齿轮锻件精度会有一定的下降。

从表3中实验效果图可以看出，脱模后的斜齿轮锻件齿形较饱满，无角隅塌陷等缺陷，在保证使用要求的前提下，只需对齿轮锻件进行稍微的倒角、打磨处理即可保证精度要求［10－11］。

5 结论

通过数值模拟与实验相结合的方法，对两种不同螺旋角的圆柱斜齿轮浮动凹模冷挤压成形及脱模进行对比分析，得出以下结论：

（1）圆柱斜齿轮采用浮动凹模工艺可有效改变摩擦力方向，降低成形载荷，与传统工艺相比，螺旋角为22°和32°的两种斜齿轮，成形力分别下降约30%和25%。

（2）通过数值模拟和铅试样实验，揭示了脱模过程中斜齿轮锻件沿着齿形螺旋方向做刚性旋转运动的现象，在一定程度上避免了脱模时凹模齿腔对锻件齿形产生的破坏性变形。

（3）影响圆柱斜齿轮成形的因素较多，其中比较显著的是螺旋角和摩擦因数，总的来说，锻件精度随着螺旋角和摩擦因数的增大而有所降低。因此，在保证使用要求的前提下，需对锻件进行一定的表面处理以保证其精度。

［1]海锦涛.塑性成形技术的新思路［J］.中国机械工程，2000，11（1／2）：180－182.

［2]王岗超，薛克敏，许峰，等.齿腔分流法冷精锻大模数圆柱直齿轮［J］.塑性工程学报，2010，17（3）：18－21.

［3]胡成亮，刘全坤，王强，等.直齿轮刚性旋转两步成形工艺仿真与试验［J］.农业机械学报，2008，39（1）：161－164.

［4]Choi J C，Choi Y，Tak S J.The Forging of Helical Gears：Comparisons of the Forging Processes［J］.International Journal of Mechanical Sciences，1999，41（6）：725－739.

［5]吴昊，伍万斌，薛克敏.圆柱斜齿轮闭式温锻数值模拟［J］.合肥工业大学学报，2008，31（1）：96－99.

［6]江雄心，万平荣，扶名福.齿轮精锻的数值模拟与实验研究［J］.塑性工程学报，2002，9（1）：62－65.

［7]俞汉清，陈金德.金属塑性成形原理［M］.北京：机械工业出版社，1999：151－153.

［8]刘华，席庆坡，霍艳军，等.圆柱齿轮精锻数值模拟及轮齿修形规律［J］.西安交通大学学报，2004，38（11）：1186－1189.

［9]朱家诚，王纯贤，等.机械设计基础［M］.合肥：合肥工业大学出版社，2003：49－54.

［10]胡成亮，刘全坤，王强，等.基于灰色关联和模糊逻辑的齿轮锻模多目标优化设计［J］.中国机械工程，2007，17（14）：1739－1742.

［11]陈永久，蒿敬恪，杜梅.机械加工技术［M］.北京：人民邮电出版社，2008：154－160.