无可信第三方的可验证多重密钥共享方案

张本慧，蒋 伟，唐元生

（扬州大学数学科学学院，江苏扬州225002）

无可信第三方的可验证多重密钥共享方案

张本慧，蒋 伟，唐元生＊

（扬州大学数学科学学院，江苏扬州225002）

提出一个无可信第三方的可验证的向量空间多重密钥共享方案，其安全性依赖于椭圆曲线密码学的安全性.该方案具有如下特点：无须可信第三方的参与，极大地减少了开销；由参与者联合生成共享的主密钥并分发相应的共享份额；可以共享多个主密钥，而每个共享者只须存储一个子密钥；可以有效防止内部成员的欺诈以及外部攻击者的攻击；仅需有限的存储空间和传输带宽，具有实际应用价值.

向量空间密钥共享；多重密钥共享；无可信第三方；椭圆曲线密码学

密钥共享是现代密码学的一个重要工具，使用密钥共享可以防止系统密钥的遗失、破坏及降低敌手破译密钥的成功率.SHAMIR［1］于1979年提出（t，n）门限密钥共享的概念，即在n个参与者中共享密钥s，当且仅当至少有t个参与者合作时才能恢复密钥s.BRICKELL［2］于1989年拓展了门限密钥共享的概念，提出向量空间密钥共享方案.但是在实际应用中，无论门限密钥共享方案还是向量空间密钥共享方案，都存在第三方和成员的欺诈问题.为了解决这些问题，一方面，有学者提出构造无可信第三方的密钥共享方案，其中大部分方案［3－6］基于门限密钥共享而设计；另一方面，CHOR等［7］提出通过构造可验证的密钥共享方案来防止第三方和内部成员的欺骗以及外部攻击者的攻击.多重密钥共享研究的主要内容是如何安全有效地共享多个密钥.本文基于向量空间密钥共享，构建了一个可验证的无须可信第三方参与的多重密钥共享方案.相比于文献［8］的方案，本文方案可共享多个密钥，同时方案中加入了验证算法，使得方案更加安全.相比于一些可验证多重密钥共享方案［9－11］，本文方案具有如下优点：无须可信第三方的参与；本文的验证算法是基于椭圆曲线密码学，而文献［9－11］方案的验证算法是基于RSA（Rivest－Shamir－Adleman）密码学；而椭圆曲线密码学的密钥长度大约是同等安全性条件下RSA密码学密钥长度的1／6［12］，所以在实际应用中本文方案仅需有限的存储空间和传输带宽.

1 预备知识

定义1（多重密钥共享方案） 设参与者集合P＝｛P1，…，Pn｝上的m个主密钥空间S1，…，Sm对应的存取结构分别为Γ1，…，Γm，S1，…，Sn分别为参与者P1，…，Pn的子密钥取值空间，U为随机输入集合.P为实现多存取结构｛Γ1，…，Γm｝的多重密钥共享方案，是指存在映射Π：S1×…× Sm×U→S1×…×Sn，使得对任意选取的m个主密钥s1∈S1，…，sm∈Sm以及随机输入u∈U，有Π（s1，…，sm，u）＝（s1，…，sn），其中si∈Si为Pi的子密钥，1≤i≤n，并且映射Π满足下列条件：

1）重构要求.对于每个i，1≤i≤m，si∈Si可被Γi的任何授权集重构，即存在重构函数族Re＝｛：（S1×…×Sn）A→Si｜1≤i≤m，A∈Γi｝，使得对任意的A∈Γi，（s1，…，sm）∈S1×…× Sm，u∈U都有（Π（s1，…，sm，u）｜A）＝si；这等价于要求对每个i，1≤i≤m和任意A∈Γi，均有H（Si｜SA）＝0，其中H（·）为熵函数.

2）安全性要求.对任意B｛P1，…，Pn｝和T｛S1，…，Sm｝＼｛Si｜B∈Γi，1≤i≤m｝，满足0＜H（T｜SB）≤H（T）；这也等价于要求对1≤i≤m的任意BΓi和T｛S1，…，Sm｝＼｛Si｝，满足0＜H（Si｜SB，T）≤H（Si｜T）.

定义2（向量空间密钥共享方案） 设Γ是参与者集合P＝｛P1，…，Pn｝上的一个存取结构，D（P）是可信的第三方.如果对于有限域K＝GF（q）上的向量空间E＝Kr，存在一个函数ψ：P∪D→E，使得A∈Γψ（D）可以由ψ（A）＝｛ψ（Pi）｜Pi∈A｝中的向量线性表示，则称Γ为P上的一个向量空间存取结构.若Γ是一个向量空间存取结构，则可构建Γ上的一个主密钥空间和子密钥空间均为有限域K的密钥共享方案：对于要共享的密钥s∈K，D随机选取向量v∈E满足v·ψ（D）＝s，D计算并秘密发送si＝v·ψ（Pi）给参与者Pi作为他的子密钥.

2 方案描述

2.1 系统初始化

1）设q是一个大素数，E（Zq）是定义在Zq上的椭圆曲线，G是E（Zq）上阶为p（p为大素数）的一个点，使得在〈G〉上的离散对数问题难处理.

2）设参与者集合P＝｛P1，…，Pn｝上的m个向量空间存取结构Γ1，Γ2，…，Γm，这里的函数ψ：P→（t＞m）满足向量ψ（Pj）中至少存在两个分量不为0，其中ψ（Pj）＝（aj1，aj2，…，ajt），j＝1，2，…，n；无可信第三方，参与者共同约定m个向量ei＝（0，…，0，0，…，0），i＝1，2，…，m，则A∈Γiei可以由ψ（A）中的向量线性表示.

2.2 密钥生成

1）每个参与者Pi随机选取xi＝（xi1，xi2，…，xit）∈（）t，计算并公开Ti1＝xi1G，Ti2＝xi2G，…，Tit＝xitG.

2）每个参与者Pi计算sij＝xi·ψ（Pj）mod p并秘密发送给参与者Pj.

3）每个参与者Pj验证他们所收到的sij：sijG＝，i＝1，2，…，n，一旦发现某个sij不满足此等式，则向Pi发出一个抱怨，作为回应，Pi公开揭示一个满足此等式的sij.

4）如果所有的sij通过了验证，则每个参与者Pj可以计算自己的子密钥为sj＝此时随机默认生成的m个主密钥即为

2.3 密钥重构

不失一般性，假设Γi中授权子集A＝｛P1，P2，…，Pl｝准备重构主密钥ki.

1）A中成员可以通过下式相互验证对方子密钥的真实性：siG＝，i＝1，2，…，l，如果所有子密钥通过了验证，则可进入步骤2）恢复主密钥，否则，协议停止.

2）首先，A中成员通过合作计算出λ1，λ2，…，λl∈Zp，使得ei＝（0，…，0，1，0，…，0）＝λ1ψ（P1）＋λ2ψ（P2）＋…＋λlψ（Pl），然后通过计算下式即可恢复主密钥ki：

3 方案分析

3.1 可行性分析

性质1 本文方案满足多重密钥共享方案定义中的重构要求.

证明 这里只须证明式（1）是正确的.事实上，ki＝mod p＝·eimod p＝·ψ（Ph）mod p＝hshmod p.

3.2 安全性分析

引理1 设t维向量ei＝（0，…，0，1i，0，…，0）不能用中的向量v1，v2，…，vr线性表示，则存在向量ai＝（ai1，…，aii，…，ait）∈且aii＝1，使得v1·ai＝0，v2·ai＝0，…，vr·ai＝0.

证明 设vj＝（vj1，vj2，…，vjt），j＝1，2，…，r，要证明存在向量ai∈且aii＝1，使得v1·ai＝0，v2·ai＝0，…，vr·ai＝0，只须证明下列方程组存在解a′i＝（ai1，…，ai，i－1，ai，i＋1，…，ait）∈：

若v1i，…，vri全为0，则方程组（2）必存在解a′i＝（0，…，0）∈；若v1i，…，vri不全为0，这等价于要证明方程组（2）的系数矩阵M与增广矩阵N有相同的秩.记r（M）为矩阵M的秩，r（N）为矩阵N的秩，下面只须证明r（M）＝r（N）.假设r（M）≠r（N），不妨设r（M）＜k，r（N）＝k，矩阵N的前k行向量线性无关，则矩阵M的前k行向量一定线性相关，从而存在一组不全为0的数h1，h2，…，hk∈Zp，使得

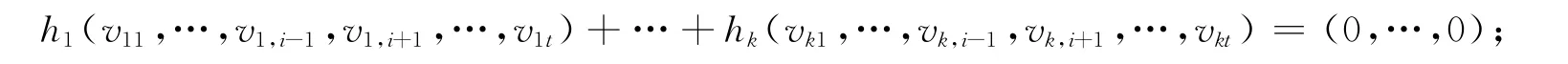
因此，β－1h1（v11，…，v1，i，…，v1t）＋…＋β－1hk（vk1，…，vk，i，…，vkt）＝（0，…，0，1，0，…，0）＝ei，这与eii不能用向量v1，v2，…，vr线性表示矛盾，从而r（M）＝r（N）.引理得证.

性质2 本文的方案满足多重密钥共享方案定义中的安全性要求.

证明 设B∈Γi但BΓj（j≠i），不妨设B＝｛P1，P2，…，Pl｝.一方面，由于BΓj（j≠i），故B中参与者无法重构主密钥kj.事实上，由引理1知：存在向量aj∈且ajj＝1，使得aj·ψ（P1）＝0，…，aj·ψ（Pl）＝0，而B中参与者拥有的关于主密钥kj的唯一信息是其中v＝＝（k1，…，kj，…，km，bm＋1，…，bt）；则对任意γ∈Zp，有即对任意∈Zp，存在向量v′＝（c1，…，…，ct）∈，使得故对B中参与者而言，Zp中的任意元素均可能是主密钥kj的值，因此他们无法正确得到kj.

另一方面，由于B∈Γi，故由性质1知，B中成员可以合作恢复出主密钥ki.B中成员要想根据ki来求得其他主密钥kj（j≠i）的值，只有存在某个向量ψ（Px），x∈｛1，2，…，l｝，使他的第i位和第j位的分量不为0，而其余分量均为0.不妨设ψ（Px）＝（0，…，0，，0，…，0，，0，…，0），此时参与者Px拥有的子密钥sx＝hiki＋hjkj，由于sx，hi，hj，ki均已知，故参与者Px可从ki处获得kj：kj＝（sx－hiki）；然而，由于B∈Γi，故ei＝（0，…，0，0，…，0）必可由ψ（B）＝｛ψ（Pi）｜Pi∈B｝中的向量线性表示，而ψ（Px）＝（0，…，0，0，…，0，…，0），因此ej＝（0，…，0，1，0，…，0）也必可由ψ（B）中的向量线性表示，与BΓj矛盾，这就表明不存在这样的ψ（Px），从而B中成员无法根据已获得的ki完全求得其他主密钥kj（j≠i）的值.

性质3 通过已知信息对方案进行攻击是不可行的.

证明 一方面，攻击者企图通过公开信息Tij＝xijG推导出xij是不可行的，因为这相当于求解椭圆曲线离散对数这一难题；另一方面，“不良”参与者企图通过sij＝xi·ψ（Pj）mod p推导出向量xi或xi的某个分量也是不可行的，因为向量ψ（Pj）至少有两个分量不为0.

性质4 外部攻击者和内部不诚实的参与者会被有效地检测出来.

证明 一方面，如果一个不诚实的参与者Pi想要欺骗参与者Pj而发送一个错误的sij，则其行为会在密钥生成之步骤3）被检测出来；另一方面，如果授权子集A∈Γi中成员想要重构密钥ki，假设A中有一个不诚实的参与者或外部存在一个攻击者“Pi”在恢复密钥时提供一个假的子密钥＝si＋ε，其中ε∈，然而在进行密钥重构之步骤1）时，A中其他参与者将会发现G≠，从而攻击行为被立即检测到.

3.3 性能分析

本文方案中没有第三方的参与，更加具有实际应用价值，因为在现实社会中要找到一个大家都信赖的人或机构作为可信第三方是非常困难的；本文方案中的验证算法是基于椭圆曲线密码学，而在达到同等安全性条件下，椭圆曲线密码学的密钥长度大约是RSA密码学密钥长度的1／6，所以本文方案仅需有限的存储空间和传输带宽；最后，当有新的参与者加入时，仅须自己选取向量xi∈（）t并计算分发共享份额，而其他参与者无须改变自己的选取参数.

［1］ SHAMIR A.How to share a secret［J］.Commun ACM，1979，22（11）：612－613.

［2］ BRICKELL E F.Some ideal secret sharing schemes［J］.J Combin Math Combin Comput，1989，9（6）：105－133.

［3］ INGEMARSSON I，SIMMONS G J.A protocol to set up shared secret schemes without the assistance of a mutually trusted party［C］／／Advances in Cryptology—EUROCRYPT’90.Lecture Notes in Computer Science.Berlin：Springer，1991，473：266－282.

［4］ PEDERSEN T P.A threshold cryptosystem without a trusted party［C］／／Advances in Cryptology—EUROCRYPT’91.Lecture Notes in Computer Science.Berlin：Springer，1991，547：522－526.

［5］ HARN L，LIN Chang－lu.Strong（n，t，n）verifiable secret sharing scheme［J］.Inf Sci，2010，180（16）：3059－3064.

［6］ HSU Ching－fang，CHENG Qi，TANG Xue－ming，et al.An ideal multi－secret sharing scheme based on MSP［J］.Inf Sci，2011，181（7）：1403－1409.

［7］ CHOR B，GOLDWASSER S，MICALI S，et al.Verifiable secret sharing and achieving simultaneity in the presence of faults［C］／／Proceedings of 26th Annual Symposium on Foundations of Computer Science.Oregon，Portland：IEEE，1985：383－395.

［8］ 唐春明，石桂花，汤永龙.没有管理者的密钥共享方案［J］.通信技术，2008，41（7）：175－182.

［9］ 刘佳，韩文报.一种安全的公开可验证门限多秘密共享方案［J］.计算机工程，2009，35（1）：24－26.

［10］ DEHKORDI M H，MASHHADI S.An efficient threshold verifiable multi－secret sharing［J］.Computer Standards ＆Interfaces，2008，30（3）：187－190.

［11］ 王斌，宋朝霞.一种有效的（t，n）门限可验证多密钥共享方案［J］.扬州大学学报：自然科学版，2009，12（3）：70－73.

［12］ 张险峰，秦志光，刘锦德.椭圆曲线加密系统的性能分析［J］.电子科技大学学报，2001，30（2）：144－147.

Abstract：A verifiable vector space multi－secret sharing scheme is proposed.Its security is based on the security of elliptic curve cryptography.This scheme has the following characteristics：there is no trusted center，so the cost can be saved greatly；all the participants cooperate to generate the secrets and distribute the corresponding shares；all participants can share multiple secrets，but each participant just needs to save one sub－key；the cheating between participants and the attack from outsiders can be detected；the current scheme is just needs limited memory and communication bandwidth，so it is valuable in practical applications.

Keywords：vector space secret sharing；multi－secret sharing；without a trusted center；elliptic curve cryptography

（责任编辑 时 光）

A verifiable multi－secret sharing scheme without a trusted center

ZHANG Ben－hui，JIANG Wei，TANG Yuan－sheng＊
（Sch of Math Sci，Yangzhou Univ，Yangzhou 225002，China）

TP 309.2

A

1007－824X（2012）02－0065－05

2011－09－29

国家自然科学基金资助项目（60971123）

＊联系人，E－mail：ystang＠yzu.edu.cn