节点含时滞的输出耦合复杂网络的自适应脉冲同步

尚 磊，仲启龙，郑永爱

（扬州大学信息工程学院，江苏扬州225127）

节点含时滞的输出耦合复杂网络的自适应脉冲同步

尚 磊，仲启龙，郑永爱＊

（扬州大学信息工程学院，江苏扬州225127）

针对节点含时滞的输出耦合动态网络模型，基于Lyapunov稳定性理论和时滞脉冲微分方程理论，设计了复杂网络同步自适应脉冲控制器，给出网络同步的充分条件，保证动态网络渐近同步于任意指定的网络中单独节点的状态，进而实现该网络的同步.理论推导和数值结果均表明该同步方法的有效性及可行性.

复杂时滞网络；自适应脉冲控制；同步；输出耦合

近年来，复杂网络的同步作为复杂网络科学的一个重要分支，备受科学研究和工程应用各个领域的关注，并且已经取得丰硕的研究成果.复杂网络节点的耦合方式主要分为两种：节点状态耦合和节点输出耦合.ZHOU［1］，GUO［2］等主要针对节点状态耦合进行了研究，但很少探讨节点输出耦合的情况.此外，时滞作为网络中的常见现象，用于描述系统当前状态变化率依赖过去状态的特性，往往导致网络在运行中出现振荡和不稳定现象.正是由于网络环境中时滞现象的普遍存在且对网络同步的影响不可忽略，因此开展对节点含时滞的复杂网络的同步研究具有重要的现实意义.研究时滞网络同步的控制方法常见的有自适应控制［3－6］、牵制控制［7］、脉冲控制［8－13］等.本文拟将自适应控制和脉冲控制相结合，利用Lyapunov稳定性理论和脉冲微分方程理论，针对节点含时滞的输出耦合复杂网络提出新的同步准则.

1 问题描述

考虑包含N个相同节点的复杂动态网络状态方程为

式中1≤i≤N，第i个节点的状态向量为xi＝（xi1，xi2，…，xin）T∈Rn，时滞状态向量为xi（tτ）＝（x1（t－τ），x2（t－τ），…，xn（t－τ））∈Rn；非线性光滑函数f：Rn→Rn；每个节点的输出矩阵H∈Rm×n；内部耦合矩阵L∈Rn×m.外部耦合矩阵C＝（cij）N×N∈RN×N，若从节点i到j（i≠j）有连接，则cij≠0；否则cij＝0，假设矩阵C满足耗散耦合条件：＝＝－cii.若limt→∞x1（t）＝limt→∞x2（t）＝…＝limt→∞xN（t），则复杂网络（1）达到同步.

设网络的同步流形为

式中s（t）∈Rn为状态向量，y∈Rm为输出变量.

假设1 LH≠0且‖LH‖2＞0，ρmax表示矩阵（LH＋HTLT）／2的最大特征值.

假设2 外部耦合矩阵cij的每个元素都是有界的，即满足｜cij｜≤C，i，j＝1，2，…，n，其中C为正常数.

假设3 非线性函数f（x（t），x（t－τ））＝［f1（x（t），x（t－τ）），…，fn（x（t），x（t－τ））］T是Lipschitz连续的，即对于x∈［x1（t），…，xn（t）］T∈Rn，y∈［y1（t），…，yn（t）］T∈Rn，存在一个常数kij，满足不等式｜fi（x（t），x（t－τ））－fi（y（t），y（t－τ））｜≤（｜xj（t）－yj（t）｜＋｜xj（t－τ）－yj（t－τ）｜），i，j＝1，2，…，n.

引理1 对于任意x，y∈Rn，ε＞0，有2xΤy≤εxΤ＋ε－1yΤy.

引理2 对于任意x∈Rn，若P∈Rn×n是正定矩阵，Q∈Rn×n是对称矩阵，则下列不等式λmin（P－1Q）xTPx≤xTQx≤λmax（P－1Q）xTPx成立，式中λmin（P－1Q），λmax（P－1Q）分别是矩阵P－1Q的最小特征值和最大特征值.

2 自适应脉冲同步

设误差ei＝xi－s（1≤i≤N），在自适应脉冲控制下，系统（1）可以表示为

式中i＝1，2，…，N，xi）和xi（t－k）分别表示xi（tk）在t＝tk时的左、右极限，其中｛tk｝满足0≤t1≤t2≤…≤tk≤…，Bik是一个n×n的常数矩阵.笔者对系统（1）设计了2个控制器：自适应控制器ui，脉冲控制器Uik.当网络实现完全同步时，耦合项消失.自适应控制器ui和自适应律di设计如下：ui＝－diei，i＝1，2，…，N；di＝e＝ki‖ei‖2，i＝1，2，…，N，ki为大于零的任意常数.

系统（1）在自适应脉冲控制器作用下的同步误差为

式中ui是须设计的自适应控制器.若控制系统（4）在原点渐近稳定，则系统（1）渐近同步.

设Sρ＝｛x∈Rn：‖x‖＜ρ，0＜ρ1≤ρ｝，K＝｛φ∈C（R＋，R＋）：φ（t）是严格递增的，且φ（0）＝0｝，K＊＝｛φ∈K：φ（t）＜t，t＞0｝，∑＝｛φ∈C（R＋，R＋）：φ（0）＝0，φ（t）＞0，t＞0｝，PC＝｛φ：［－τ，0］→R｝，φ（t）是除有限个点之外处处连续的，在珋t处，有φ（珋t＋）和φ（珋t－）存在，且φ（珋t＋）＝φ（珋t）.

系统（4）可以转化为以下微分方程：

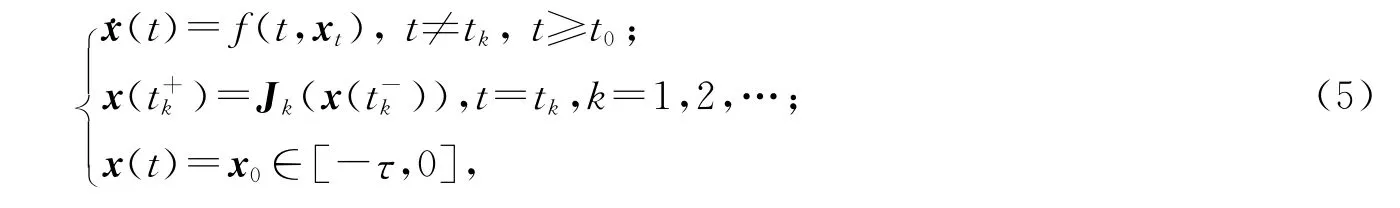
这里f：［0，∞］×PC→Rn.为确保方程（5）有一个零解，Jk（x）：Sρ→Rn且Jk（0）＝0，xt（s）＝x（t＋s），s∈［－τ，0］.

引理3［10］248假设存在V∈V0，ω1，ω2∈K，φ∈K＊和H∈Σ，并满足以下条件，则方程（5）的零解一致渐近稳定：

1）ω1（‖x‖）≤V（t，x（t））≤ω2（‖x‖），（t，x）∈［t0，∞）×Sρ；

2）对于所有的x∈Sρ1，0＜ρ1≤ρ和任意的k，V（tk，J（tk））≤φ（V（t－k，x））成立；

3）对于方程（4）的任意解x（t），若V（t＋s，x（t＋s））≤φ－1（V（t，x（t））），－τ≤s≤0，则D＋（V（t，x（t）））≤g（t）H（V（t，x（t））），这里g：［t0，∞）→R＋局部可积，φ－1是φ的逆函数；

4）H是非减的，A＞0和常数λ2≥λ1＞0，满足任意的μ＞0，λ1≤tk－tk－1≤λ2和（s）ds≥A成立.

3 同步化准则

定理1 假设1，2，3和引理1，2均成立，如果存在α和bik，对于i＝1，2，…，N和k∈Z＋＝｛1，2，…，＋∞｝都满足如下条件，则自适应脉冲控制下节点含时滞的输出耦合网络（1）渐近同步：

1）－2＜bik＜0；

2）p＋q／max1≤i≤N｛（1＋bik）2｝≤α，其中p＝max1≤i≤N，1≤j≤N2（kij＋CNρmax－di），q＝max1≤i≤N，1≤j≤N2kij；

3）α（tk－tk－1）＋ln［max1≤i≤N（1＋bik］2）＜0.

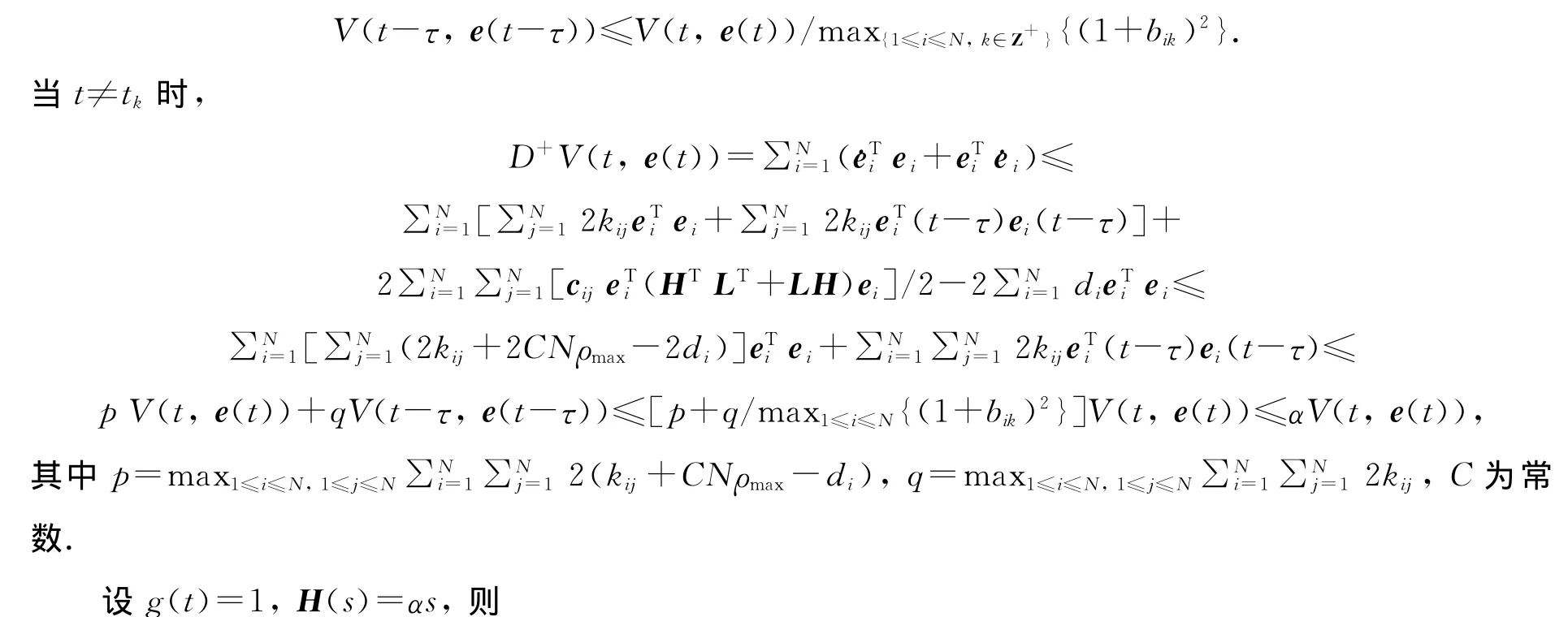
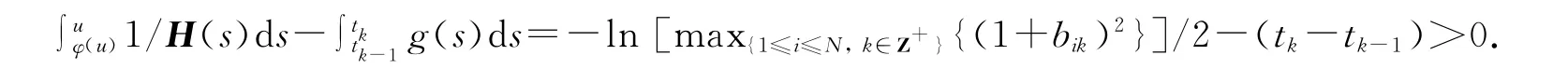
其余证明类似于文献［14］定理1的证明，从而得出自适应脉冲控制下节点含时滞输出耦合网络（1）是渐近同步的.

4 数值仿真

1）对3个时滞Logistic系统为节点组成的网络进行数值仿真，该系统的状态方程为xi＝－λxi＋rxi（t－τ）（1－xi（t－τ）），1≤i≤3；系统有2个平衡点：s1＝0，s2＝1－λ／r；当λ＝26，r＝104，τ＝0.5时，系统处于混沌状态；耦合函数为LHxj.选取系统的s2＝1－λ／r＝1－26／104＝0.75作为同步目标，由于系统中m＝n＝1，所以矩阵H和L是两个数值，取H＝3，L＝4，则ρmax＝12；选择kij＝1＞0，di＝50＞0，C＝（cij）3×3取满足耗散耦合条件的，由定理1可得bik＝－0.9，α≥198，Δt＜0.023.仿真中取α＝200，Δt＝0.01，仿真结果如图1～2所示.图1表明在自适应脉冲控制下网络节点很快同步，图2表明当误差趋于零后自适应律趋于一个稳定的常数值.

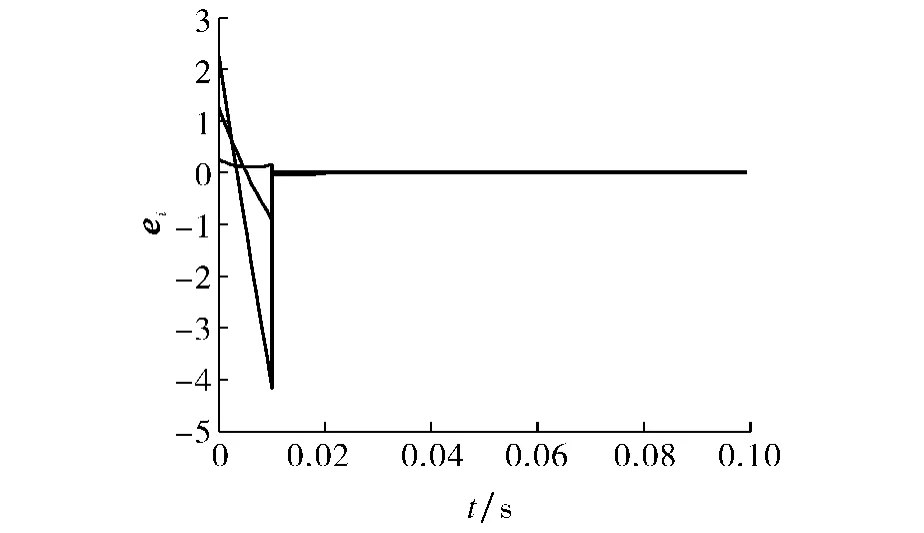
图1 仿真1中的自适应脉冲同步误差Fig.1 The synchronization errors of adaptive－impulsive control in simulation 1

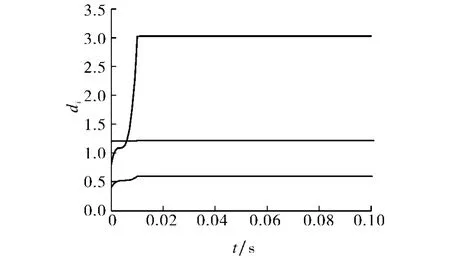
图2 仿真1中的自适应律Fig.2 Adaptive law in simulation 1

2）考虑10个节点组成的时滞网络模型，其中每个节点的状态方程为

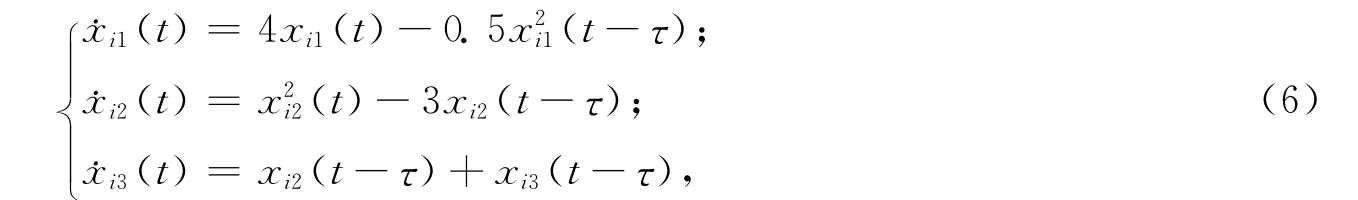
式中1≤i≤10，其耦合函数为∑Nj＝1cijLHxj.仿真中取τ＝2，H＝diag（4，3，2），L＝diag（1，2，3），则ρmax＝6，kij＝1＞0，di＝500＞0，C＝（cij）10×10取满足耗散耦合条件的，由定理1可得bik＝－0.95，α≥362，Δt≤0.014 98.仿真中取α＝400，Δt＝0.01，仿真结果如图3～4所示.图3表明在自适应脉冲控制下网络节点很快同步，图4表明当误差趋于零后自适应律趋于一个稳定的常数值.

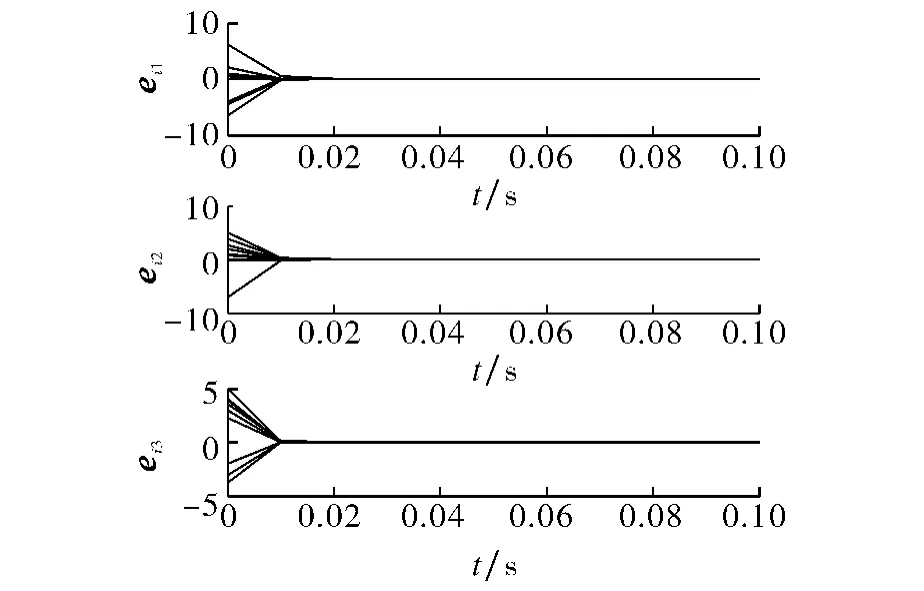
图3 仿真2中的自适应脉冲同步误差Fig.3 The synchronization errors of adaptive－impulsive control in simulation 2

图4 仿真2中的自适应律Fig.4 Adaptive law in simulation 2

［1］ ZHOU Jin，CAI Shui－ming，XIANG Lan.Robust impulsive sychronization of uncertain delayed dynamical networks［C］／／7th World Congress on Intelligent Control and Automation（WCICA）.Chongqing：［s.n.］，2008：1901－1906.

［2］ GUO Wan－li，AUSTIN F，CHEN Shi－hua.Global synchronization of nonlinearly coupled complex networks with non－delayed and delayed coupling［J］.Commun Nonlinear Sci Numer Simul，2010，15（6）：1631－1639.

［3］ 罗群，吴薇，李丽香，等.节点含时滞的不确定复杂网络的自适应同步研究［J］.物理学报，2008，57（3）：1529－1534.

［4］ 杨彦清.时变耦合复杂网络同步的自适应控制［J］.微计算机信息，2010，26（2／1）：205－206.

［5］ ZHOU Jin，LU Jun－an，LV Jin－hu.Adaptive synchronization of an uncertain complex dynamical network［J］.IEEE Trans Autom Control，2006，51（4）：652－656.

［6］ 赵磊，胡冯仪，郑永爱，等.不同混沌系统的自适应混合投影同步［J］.扬州大学学报：自然科学版，2008，11（3）：45－48.

［7］ 樊春霞，蒋国平.输出耦合的复杂网络自适应牵制同步［J］.应用科学学报，2010，28（2）：203－208.

［8］ CAI Shui－ming，ZHOU Jin，XIANG Lan，et al.Robust impulsive synchronization of complex delayed dynamical networks［J］.Phys Lett A，2008，372（30）：4990－4995.

［9］ 樊春霞，蒋国平，程艳云.耦合时延复杂网络的无源脉冲同步［J］.应用科学学报，2007，25（6）：594－597.

［10］ YAN Ju－rang，SHEN Jian－hua.Impulsive stabilization of functional differential equations by Lyapunov－Razumikhin functions［J］.Nonlinear Anal：Theory Methods Appl，1999，37（2）：245－255.

［11］ ZHOU Jin，WU Quan－jun，XIANG Lan，et al.Impulsive synchronization seeking in general complex delayed dynamical networks［J］.Nonlinear Anal：Hybird Syst，2011，5（3）：513－524.

［12］ ZHAO Yan－hong，YANG Yong－qing.The impulsive control synchronization of the drive－response complex system［J］.Phys Lett A，2008，372（48）：7165－7171.

［13］ WAN Xiao－jun，SUN Ji－tao.Adaptive－impulsive synchronization of chaotic systems［J］.Math Comput Simul，2011，81（8）：1609－1617.

［14］ LI Ping，CAO Jin－de，WANG Zi－dong.Robust impulsive synchronization of coupled delayed neural networks with uncertainties［J］.Phys A：Stat Mech Appl，2007，373（1）：261－272.

Abstract：This paper mainly studies a complex delayed network coupled with the outputs.Based on Lyapunov stability theory and the theory of impulsive delayed differential equation，it designs an adaptive－impulsive controller of the network realizing synchronization.Then it gives the sufficient conditions of synchronization on networks，guarantees that the dynamical network asymptotically synchronizes at the individual node state in arbitrary specified network，and realizes the synchronization of networks.Furthermore，both the theoretical analysis and the results of numerical simulations illuminate the validity and feasibility of the synchronized method.

Keywords：complex delayed networks；adaptive－impulsive control；synchronization；the output coupled

（责任编辑 林 子）

Adaptive－impulsive synchronization of complex delayed networks coupled with the outputs

SHANG Lei，ZHONG Qi－long，ZHENG Yong－ai＊
（Sch of Inf Engin，Yangzhou Univ，Yangzhou 225127，China）

TP 273.2；O 175.26

A

1007－824X（2012）02－0060－05

2012－01－10

国家自然科学基金资助项目（61074129）

＊联系人，E－mail：zhengyongai＠163.com