离散时间模型的指数效用无差别定价

刘利敏，王宣涛

（河南师范大学数学与信息科学学院，河南新乡453007）

离散时间模型的指数效用无差别定价

刘利敏＊，王宣涛

（河南师范大学数学与信息科学学院，河南新乡453007）

利用鞅方法证明了完全市场的指数效用函数无差别定价为无套利定价，讨论了不完全市场中指数效用函数无差别定价计算的关键问题，得到三叉树模型的指数效用无差别定价为特定鞅测度下未定权益期末收益的变异条件期望.

完全市场；不完全市场；指数效用函数；无差别定价

效用无差别定价是一种未定权益定价的新方法，首先由HODEGES，NEUBERGER［1］提出.近年来，关于指数效用函数无差别定价的研究获得了很多成果.例如，刘利敏［2］，MUSIELA［3］，李玉萍［4］，BENTH［5］，BECHERER［6］，闫海峰［7－8］等探讨了连续时间模型的指数效用无差别定价；MUSIELA［9］，刘利敏［10］等则研究了特殊离散时间模型未定权益的指数效用无差别定价.由于针对离散时间模型的系统研究比较少，因此本文拟利用鞅方法对离散时间模型的完全市场指数效用无差别定价进行讨论，应用动态规划方法研究特殊模型的不完全市场效用无差别定价.

1 完全市场的指数效用无差别定价

对于离散时间模型，存在T＋1个交易日0，1，…，T，T为未定权益的到期日.市场中的信息流F＝｛Ft｝.市场中存在两种资产：一是无风险资产Bt，二是风险资产St＝（S1（t），S2（t），…，SN（t））.交易策略α（t）＝（α0（t），α1（t），…，αN（t））构成的集合记为Αt，财富过程记为X＝｛Xt｝.

假设市场是完全的无摩擦的金融市场，则市场中存在唯一的等价鞅测度Q.给定未定权益CT，考虑如下最优投资组合问题：

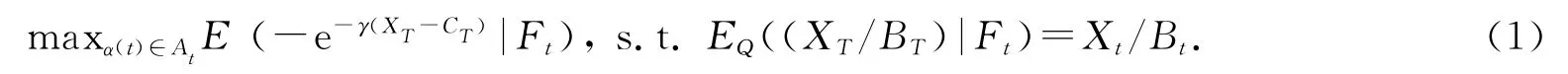
记上述最优投资问题的价值函数为VCT（Xt／Bt，XT－CT）.若CT＝0，则记为V0（Xt／Bt，X）.

定义1 给定未定权益CT，满足V0（Xt／Bt，XT）＝VCT（Xt／Bt＋υt／Bt，XT－CT）的υt称为未定权益CT在t时刻的指数效用无差别定价.

定理1 在离散的完全市场中未定权益CT在t时刻的指数效用无差别定价为υt／Bt＝EQ（（CT／BT）｜Ft）.

其中LT＝QT／PT.由一阶条件得

2 不完全市场的指数效用无差别定价

由于指数效用无差别定价计算的关键在于求解最优问题

其中Χ≡｛XT∈Rk：EQ（（XT／BT）｜Ft）＝Xt／Bt，Q∈Μ｝，Μ是等价鞅测度的集合，其对应的价值函数记为VCT（Xt／Bt，XT－CT）.

如果模型是不完全的，则风险中性概率测度集合包含无穷多个元素.由于Μ是一个线性子空间，因此存在着珡Μ（即Μ的闭集）中的有限个独立变量Q（1），Q（2），…，Q（J），使得Μ中的每一个元素能表示为这J个变量的线性组合，且权重之和为1；从而对于所有的Q∈Μ，EQ（XT／BT）＝Xt／Bt成立当且仅当EQ（j）（XT／BT）＝Xt／Bt，于是Χ≡｛XT∈Rk：EQ（j）（（XT／BT）｜Ft）＝Xt／Bt，j＝1，…，J｝.由此可得最优组合问题（5）表示为

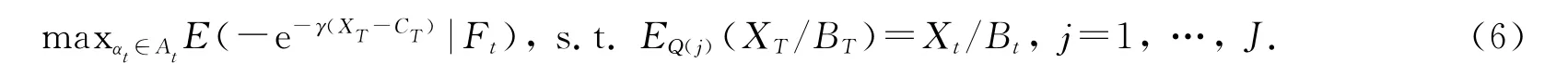
问题（6）能通过引入拉格朗日乘子求解，同时J对应于状态价格密度Lj≡Q（j）／P使得

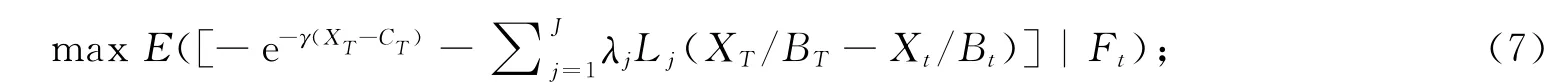
但是，由于拉格朗日乘子的增多，（7）式的最优财富过程较为复杂，故很难得到价值函数的显式解.

3 一个例子

由于问题（5）的价值函数很难得到显式解，因此不完全市场的无差别定价难以求出；然而，对于一些特殊的模型，可以利用动态规划方法求出其无差别定价，三叉树模型就是其中一种.

在一个单时期三叉树模型中，假设无风险资产恒为1，风险资产在0时刻的价值表示为S0，期末时刻为ST.设Ω＝｛ω1，ω2，ω3｝，对任意i＝1，2，3，pi＝P｛ωi｝＞0，ST（ω1）＝，ST（ω2）＝S0，ST（ω3）＝，其中0＜ξd＜1＜.假设投资者的初始财富为X0＝x，投资者在初始时刻购买α份股票，则期末时刻投资者的财富为XT＝β＋αST＝（x－αS0）＋αST＝x＋α（ST－S0）.给定未定权益CT，记

本文以南方某区域为例进行分析，同时以全国该领域平均水平为依据进行相关原则制定。由于篇幅限定，本文不再一一列举相关数据。针对文中的评价对象，主要依据南方地区数据为依据，一些定量数据主要通过国家统计局、气象局、行业协会等获得；针对一些定性的指标主要通过模糊评判集的方法进行量化[4]，在百分制中以20为单位进行划分五个区间，即0～20，>20～40，>40～60，>60～80，>80～100，从而将定性指标量化在该区间中，以表示该地区的对应指标发展情况。19个电能替代领域排名如表3所示。最后依据综合排名前十一位为大力发展电能替代技术。

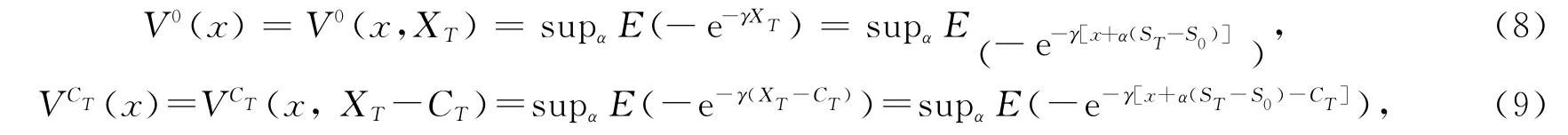
且问题（8）和（9）的最优策略分别记为α0和αCT.

未定权益在T时刻的收益为CT＝C（ST），记CT（ωi）＝ci∈R，i＝1，2，3.首先计算VCT（x）.由于

其中A＝p2／［q－qp13－q（1－q）q－1＋p2］，BT＝｛ω1，ω3｜ST｝，由Q的定义可以得到υ＝γ－1· ln ［EQ（）］.

定理2 单时期三叉树模型的指数效用无差别定价为υ＝γ－1ln ［）］，其中Q满足（12）式.

在多时期的三叉树模型中，假设有T＋1个交易日.随机过程St，t＝0，1，…，T表示被交易的风险资产在t时刻的价格，假设St＞0，ξt＋1＝St＋1／St，其中ξt＋1＝，1，，0＜＜1＜ξ.｛St：t＝0，1，…，T｝是概率空间（Ω，（Ft），P）上的一维随机过程，且Ft＝σ（St）.设Xt表示［t－1，t］的财富过程，X0＝x，αt表示在［t－1，t］时间段进行交易的资产份额，则Xt＝Xt－1＋αt（St－St－1）.记

则t时刻的效用无差别价格υt是一个Ft适应的随机变量，满足

现在定义一个新的测度Q，满足t＝0，1，…，T时，

Q（St＝｜Ft－1）＝qtAt，Q（St＝St－1｜Ft－1）＝1－At，Q（St＝｜Ft－1）＝（1－qt）At，（15）其中At＝（1－q］／＋p2t］，qt＝（－＋1）／（），p1t＝P（St＝｜Ft－1），p2t＝P（St＝St－1｜Ft－1），p3t＝P（St＝｜Ft－1）.令Bt＝｛ξt＝或ξt＝｝，＝σ（Bt），下面定义一个新的迭代函数.对于任意Ft适应过程Zt，满足

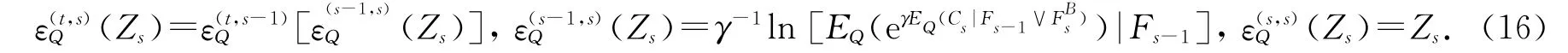
定理3 假设测度Q满足（15）式，如果pq1ttqt－qtp13t－qt（1－qt）qt＝p2t，则在t时刻未定权益CT的无差别定价为

而且υT还满足如下迭代关系：

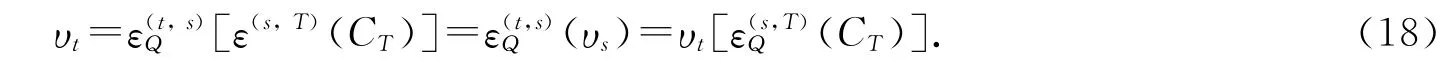
证明 首先证明当t＝T－1时，（17）式成立，剩下的利用数学归纳法证明.因为

VCT（XT－1，T－1；T）＝e－γXT－1supαT［－－］，与单阶段类似，得VCT（XT－1，T－1；T）＝－e－γXT－1－hT－1＋，V0（XT－1，T－1；T）＝，其中qT＝［－（1－k2）＋（1＋k1）］／［（1－k2）（）］，hT－1＝－ln［·（1－qT）－1＋qT＋p2T］，λT－1（CT）＝＝γ－1ln［EQ（eγEQ（CT｜FT－1）｜FT－1］.由（14）式可得（17）式成立.

下面证明（18）式.只须证明t＝T－2，s＝T－1时（18）式成立，其余可通过数学归纳法证明.由（13）式得（XT－2，T－2；T）＝supEP（｜FT－2），将－γ－1hT－1＋υT－1作αT－1为CT－1，利用（XT－1，T－1；T）的计算方法直接得到（XT－2，T－2；T）＝，其中μ（C）＝γ－1ln［E（）｜F］.又由（14）式T－2TQT－2

可得

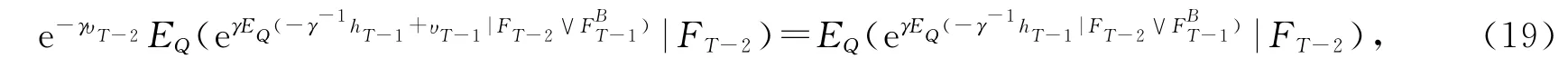
由于

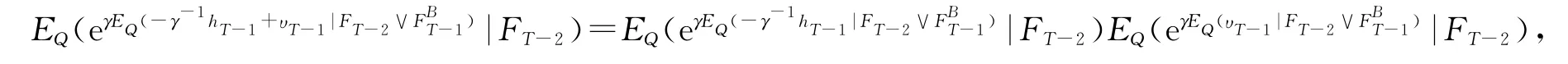
故代入（19）式可得T－2时刻的无差别价格为υT－1＝γ－1ln［EQ（eγEQ（υT－1｜FT－2）｜FT－2］.证毕.

［1］ HODGES S，NEUBERGER A.Optimal replication of contingent claims under transaction costs［J］.Rev Futures Mark，1989，8：222－239.

［2］ 刘利敏，牛保青，闫海峰.幂效用函数的无差别定价和套期保值［J］.数学的实践与认识，2009，39（5）：42－46.

［3］ MUSIELA M，ZARIPHOPOULOU T A.An example of indifference prices under exponential preferences［J］.Finance Stochast，2004，8（2）：229－239.

［4］ 李玉萍，刘利敏.非交易资产未定权益的无差别定价［J］.扬州大学学报：自然科学版，2005，8（3）：20－22.

［5］ BENTH F E，KARLSEN K H.A PDE representation of the density of the minimal entropy martingale measure in stochastic volatility markets［J］.Stochast：Int J Pro Stochast Processes，2005，77（2）：109－137.

［6］ BECHERER D.Utility－indifference hedging and valuation via reaction－diffusion systems［J］.Proc R Soc Lond Ser A：Math Phys Eng Sci，2004，460（2041）：27－51.

［7］ 闫海峰，刘利敏，杨建奇.随机波动率模型的效用无差别定价和套期保值策略［J］.系统工程学报，2007，22（4）：379－385.

［8］ 闫海峰，刘利敏，杨建奇.随机波动率模型的最小熵鞅测度和效用无差别定价［J］.工程数学学报，2009，26（1）：43－50.

［9］ MUSIELA M，ZARIPHOPOULOU T A.A valuation algorithm for indifference prices in incomplete markets［J］.Finance Stochast，2005，9（3）：399－414.

［10］ 刘利敏，王宣涛.带交易费用的指数效用无差别定价和套期保值策略［J］.应用概率统计，2011，27（6）：587－596.

Abstract：It is shown that the indifference pricing is arbitrage－free pricing by the martingale approach.The key problems about the exponential utility function indifference pricing are considered in the incomplete market，and the indifference pricing is expressed as the conditional variation expectation of contingent claim under the specific martingale measure at the terminal date.

Keywords：complete market；incomplete market；the exponential utility function；indifference pricing

（责任编辑 时 光）

The indifference pricing of the exponential utility function in the discrete time model

LIU Li－min＊，WENG Xuan－tao
（Coll of Math ＆Inf Sci，Henan Norm Univ，Xinxiang 453007，China）

O 211.6；F 830.9

A

1007－824X（2012）02－0020－04

2010－11－11

河南省教育厅软科学研究基金资助项目（2009A630026）

＊联系人，E－mail：llim2004＠163.com