S＝1铁磁模型中阻挫和各向异性引起的量子相变

李俊英，彭晓亮，潘丽华，刘拥军

（扬州大学物理科学与技术学院，江苏扬州225002）

S＝1铁磁模型中阻挫和各向异性引起的量子相变

李俊英，彭晓亮，潘丽华，刘拥军＊

（扬州大学物理科学与技术学院，江苏扬州225002）

利用密度矩阵重整化群（density matrix renormalization group，DMRG）方法研究近邻作用为铁磁耦合、次近邻为反铁磁耦合的一维S＝1的各向异性海森堡自旋模型.计算了该系统的基态能、z轴自旋关联函数和面内自旋关联函数.结果表明：各向异性值Δ和阻挫α的相互作用使得系统基态发生相变；在低阻挫区域，Δ＞1时系统为铁磁相，0＜Δ＜1时基态处于自旋液体相；在阻挫较大的区域，自旋关联函数随距离的增大呈现指数函数形式衰减，且具有周期振荡特征，与自旋S＝1／2的结果形成鲜明的对比.

密度矩阵重整化群；阻挫；各向异性；铁磁海森堡模型；自旋关联

近20年来，一维或准一维自旋系统基态的性质一直吸引着人们的关注.在此类系统中，量子涨落和阻挫等因素的相互作用使得系统呈现出丰富、复杂且无经典对应的量子态.按照HALDANE猜想［1］，在一维均匀的反铁磁系统中，自旋S为整数的系统是有能隙的，自旋关联函数随着距离的增大以指数函数形式衰减.反之，当自旋S为半整数时，系统是没有能隙的，自旋关联函数随着距离的增大以幂次函数形式衰减.此外，n条一维反铁磁S＝1／2自旋链平行排列且相互耦合组成n条链的梯子模型［2－3］.n为奇数的梯子系统与S＝1／2单链系统的性质类似：无能隙且自旋关联函数随着距离的增大以幂次函数形式衰减；而n为偶数的梯子体系是有能隙的，自旋关联函数随着距离的增大以指数函数形式衰减.近年来，Rb2Cu2Mo3，NaCu2，LiCuV等一些新材料的出现又掀起一股研究热潮.这些材料中都包含边共享的CuO2链，自旋局域于铜离子处位置，且最近邻自旋间铁磁相互作用、次近邻自旋间存在一定的反铁磁相互作用.另外，实验显示LiCuVO4相互作用存在一定的各向异性［7－8］；所以，最近邻铁磁耦合、次近邻反铁磁耦合（简称铁磁－反铁磁）的各向异性（Jx＝Jy≠Jz，XXZ）量子自旋链开始被人们关注.已有研究者［9－15］报道了自旋S＝1／2的铁磁－反铁磁XXZ自旋链的基态相图.经典理论说明除铁磁相外，还会出现反铁磁奈尔相和螺旋无共度相.最近，PLEKHANOV等［15］将相图空间细划成铁磁相、两个自旋关联函数随距离的增大呈幂次函数形式衰减、无能隙的自旋液体相和两个自旋关联函数随距离的增大呈指数函数形式衰减、有能隙的相.在本文中，笔者将利用DMRG方法进一步探讨一维S＝1的铁磁－反铁磁各向异性海森堡自旋模型的基态相图.

1 研究模型和方法

本文研究的模型如图1（a）所示，模型的哈密顿量为

其中si表示在格点i处的自旋算符；N为系统的格点数；J1＜0为近邻铁磁关联强度，J2＞0为次近邻反铁磁关联强度；Δ＞0表示近邻各向异性强度.本文取J1＝－1.0，并定义α＝｜J2／J1｜为阻挫强度.这种一维铁磁－反铁磁模型可以等效为链间铁磁关联、链上反铁磁关联的两条链的梯子模型［图1（b）］.

在模型（1）中，若J2＝0，即只有近邻相互作用，则为简单的铁磁链.［16］值得注意的是，各向同性的铁磁基态是（N＋1）重简并，而加入异轴各向异性后，铁磁基态只有两重简并，格点处所有的自旋全部朝上（spins up）或朝下（spins down），因此可以认为是异轴各向异性解除部分简并.若不考虑近邻各向异性，即Δ＝1，则模型退化为各向同性的铁磁－反铁磁海森堡链.该系统在临界点Jc＝1／4处存在一阶相变：当0＜J＜Jc时，基态为铁磁态（ferromagnetic state）；当J＞Jc时，基态为自旋单态（singlet incommensurate state）.

图1 模型（1）的结构图（a）和等价的两条链的zigzag梯子结构（b）Fig.1 （a）One dimensional chain of the model（1），（b）mapping on a two－leg zigzag ladder

通过密度矩阵重整化群的数值方法［17］，开放边界条件，保留的密度矩阵块的最小维度M＝200，同时截断误差达到10－7，增大保留的态数可以提高计算的精度.本文主要通过分析各个参数条件下基态能及z轴自旋－自旋关联函数和面内自旋－自旋关联函数随格点间距的衰减行为，得到一个完整的基态能相图.相距为r的两格点的自旋关联函数的定义为：z轴关联函数（也称对角关联函数）〉和面内自旋关联函数（也称非对角关联函数）.为了减小边界效应，在计算两个格点间的关联函数时，一般尽可能对称地从链的中间格点取值.

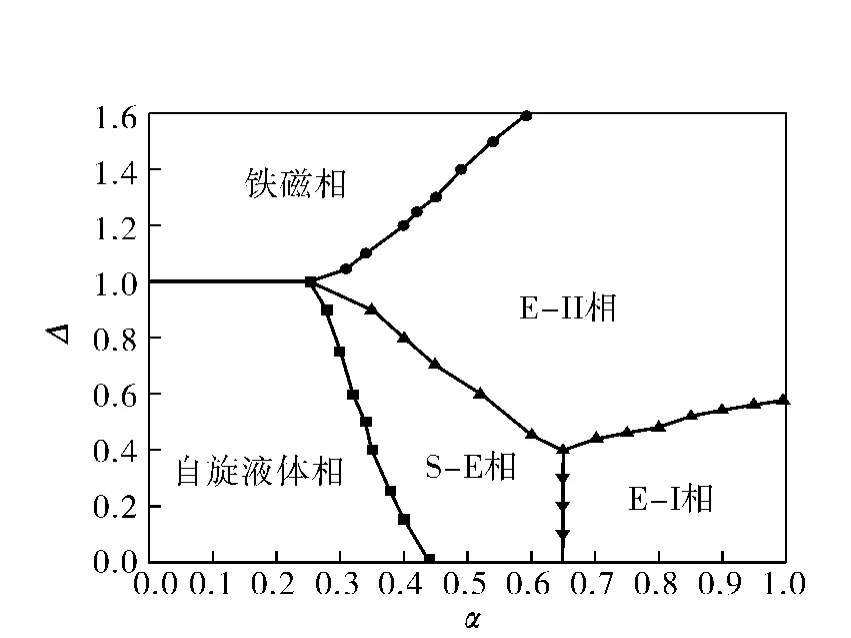
图2 S＝1的各向异性的铁磁－反铁磁海森堡模型在（α，Δ）空间的相图Fig.2 Quantum phase diagram of the anisotropic ferromagnetic－antiferromagnetic spin－1Heisenberg chain in the（α，Δ）plane

2 量子相图

系统基态相图如图2所示.由图2可见：①在低阻挫区域，Δ＞1时系统为铁磁相（ferro）；0＜Δ＜1时基态处于自旋液体相（spin－fluid）；因此，在低阻挫区域，系统行为与S＝1／2各向异性铁磁－反铁磁模型相似；②但在阻挫较大的区域，系统基态与对应的S＝1／2的基态相图有很大区别，不再存在关联函数随距离的增大呈幂次函数形式衰减的自旋液体相区域；基态自旋关联函数随距离的增大呈指数函数形式衰减特征，且存在周期振荡行为；③相图中取阻挫区间为0＜α＜1，如果反铁磁阻挫更大，则系统等效于两个铁磁耦合的反铁磁自旋链，其行为类似于一维是S＝1的海森堡自旋链.Δ＞1时，随着阻挫的增强，基态从铁磁相转变到E－II相，基态能在临界点的一阶导数有奇点，该过程为一级相变；0＜Δ＜1时，随着阻挫的增强，基态从自旋液体相转变为S－E相，基态能在临界点的二阶导数有奇点，该过程为二级相变.

2.1 自旋液体相

自旋液体相也称XXZ相，因为此相的性质类似于反铁磁XXZ模型基态能的性质，其关联函数典型的行为如图3所示.由图3可见，自旋关联函数呈幂次函数形式衰减规律，其中在xy平面处于不同位置格点处自旋的排列呈反铁磁排列，面内自旋关联函数满足～（－1，z轴关联函数的自旋在z方向呈铁磁排列，满足.

2.2 S－E相

如图4所示，S－E相与自旋液体相及E－I相连接，其关联函数的特征为：z轴关联函数随距离的增大呈现指数函数形式衰减，但面内关联函数随距离的增大呈现一定的准长程序.当异性强度Δ＜1时，随着阻挫的增强，系统依次经历自旋液体相→S－E相、S－E相→E－I相的转变.

2.3 E－I相和E－II相

在E－I相和E－II相中，轴关联函数和面内关联函数随距离的增大均呈指数函数形式衰减；但是，自旋关联函数在随距离增大而呈现指数函数形式衰减的过程中，还出现了周期性的振荡行为，其中E－I相仅面内关联函数具有振荡行为（图5），而E－II相中轴关联函数和面内关联函数都具有振荡行为（图6），且随着参数的变化振荡的周期也发生变化.

图3 Δ＝0.2，α＝0.1时自旋液体相的z轴关联函数和面内关联函数Fig.3 z－Axis and in－plane correlations in the spin－fluid phase atΔ＝0.2，α＝0.1

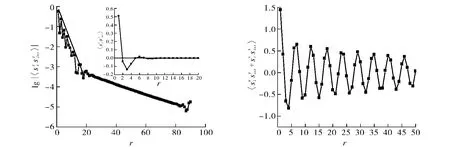
图4 Δ＝0.4，α＝0.5时S－E相的z轴关联函数和面内关联函数Fig.4 z－Axis and in－plane correlations in the S－E phase atΔ＝0.4，α＝0.5

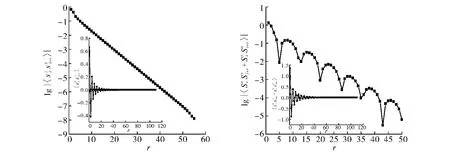
图5 Δ＝0.2，α＝0.8时E－I相的z轴关联函数和面内关联函数Fig.5 z－Axis and in－plane correlations in the E－I phase atΔ＝0.2，α＝0.8

图6 Δ＝0.9，α＝0.6时E－II相的z轴关联函数和面内关联函数Fig.6 Correlation in z－axis and in－plane correlations in the E－II phase atΔ＝0.9，α＝0.6

E－I和E－II相中关联函数出现周期性振荡行为的原因，可以归结为铁磁关联和反铁磁关联之间竞争的结果.如果阻挫足够大，则模型（1）可等价为：两条S＝1的反铁磁海森堡自旋链链间自旋存在铁磁性耦合，此时自旋关联函数呈现指数函数形式衰减，与一维S＝1反铁磁海森堡自旋链的关联函数衰减行为类似，没有振荡特征.另外，该区域自旋关联函数的行为也与经典理论中讨论的螺旋无共度相吻合：自旋关联函数傅里叶变换得到的静态结构因子S（k）出现两个峰，而一维反铁磁海森堡模型的静态结构因子仅有k＝π的峰.

［1］ HALDANE F D M.Nonlinear field theory of large－spin Heisenberg antiferromagnets：semiclassically quantized solitons of the one－dimensional easy－axis Neel state［J］.Phys Rev Lett，1983，50（15）：1153－1156.

［2］ DAGOTTO E，RICE T M.Surprises on the way from 1Dto 2Dquantum magnets：the novel ladder materials［J］.Science，1996，271（52497）：618－623.

［3］ 陆文彬，潘丽华，刘拥军.1／5掺杂反铁磁海森堡自旋链的基态［J］.扬州大学学报：自然科学版，2009，12（4）：26－30.

［4］ HASE M，KUROE H，OZAWA K，et al.Magnetic properties of Rb2Cu2Mo3O12including a one－dimensional spin－1／2Heisenberg system with ferromagnetic first－nearest－neighbor and antiferromagnetic second－nearestneighbor exchange interactions［J］.Phys Rev B，2004，70（10）：104426：1－6.

［5］ DRECHSLER S L，RICHTER J，GIPPIUS A A，et al.Helical ground state and weak ferromagnetism in the edge－shared chain cuprate NaCu2O2［J］.Europhys Lett，2006，73（1）：83－89.

［6］ ENDERLE M，MUKHERJEE C，FAK B，et al.Quantum helimagnetism of the frustrated spin－1／2chain LiCuVO4［J］.Europhys Lett，2005，70（2）：237－243.

［7］ KRUG VON NIDDA H A，SVISTOV L E，EREMIN M V，et al.Anisotropic exchange in LiCuVO4probed by ESR［J］.Phys Rev B，2002，65（13）：134445：1－7.

［8］ VASI’EV A N，PONONARENKO L A，MANAKA H，et al.Magnetic and resonant properties of quasi－onedimensional antiferromagnet LiCuVO4［J］.Phys Rev B，2001，64（2）：024419：1－5.

［9］ DMITRIEV D V，KRIVNOV V Ya.Multimagnon bound states in an easy－axis frustrated ferromagnetic spin chain［J］.Phys Rev B，2009，79（5）：054421：1－10.

［10］ DMITRIEV D V，KRIVNOV V Ya.Weakly anisotropic frustrated zigzag spin chain［J］.Phys Rev B，2008，77（2）：024401：1－8.

［11］ HIKIHARA T，KABURAGI M，KAWAMURA H.Ground state phase diagrams of frustrated spin－S XXZ chains：chiral ordered phases［J］.Phys Rev B，2001，63（17）：174430：1－11.

［12］ SOMMA R D，ALIGIA A A.Phase diagram of the XXZ chain with next－nearest－neighbor interactions［J］.Phys Rev B，2001，64（2）：024410：1－4.

［13］ HEIDRICH－MEISNER F，MCCULLOCHI P，KOLEZHUK A K.Phase diagram of an anisotropic frustrated ferromagnetic spin－1／2chain in a magnetic field：a density matrix renormalization group study［J］.Phys Rev B，2009，80（14）：144417：1－9.

［14］ SOHEILIAN F，SOLTANI M R.Ground state phase diagram of the 1DXXZ model in a transverse magneticfield［J］.Indian J Phys，2010，84（3）：257－264.

［15］ PLEKHANOV E，AVELLA A，MANCINI F.The phase diagram of the extended anisotropic ferromagneticantiferromagnetic Heisenberg chain［J］.Eur Phys J B，2010，77（3）：381－392.

［16］ CLOIZEAUX J D，GAUDIN M.Anisotropic linear magnetic chain［J］.J Math Phys，1996，7（8）：1384－1400.

［17］ WHITE S R.Density－matrix algorithms for quantum renormalization groups［J］.Phys Rev B，1993，48（14）：10345－10356.

Abstract：By using the density matrix renormalization group（DMRG）method，the author investigates the diagram of the one－dimensional frustrated anisotropic ferromagnetic S＝1Heisenberg spin model，in which the nearest neighboring interactions are anisotropic ferromagnetic and the next nearest neighboring exchanges are considerable anti－ferromagnetic.The ground state energy and both the in－plane and out－of－plane spin correlation functions are calculated.Apart from the ferromagnetic phase and the spin－fluid phase in the small frustration region，but in the large frustration region，it is identified that spin correlations decay with a short－range exponential law and an oscillating behavior.The result is different from the previous result for S＝1／2.

Keywords：density matrix renormalization group；frustration；anisotropy；Heisengberg model；spin correlation function

（责任编辑 时 光）

Quantum phase transition caused by the frustration and anisotropic effect in the S＝1ferromagnetic model

LI Jun－ying，PENG Xiao－liang，PAN Li－hua，LIU Yong－jun＊（Sch of Phys Sci ＆Tech，Yangzhou Univ，Yangzhou 225002，China）

O 413.1

A

1007－824X（2012）02－0029－05

2012－02－22

江苏省科技支撑计划（工业）项目（BE2009106）

＊联系人，E－mail：yjliu＠yzu.edu.cn