基于Neyman-Pearson准则的自适应门限干扰抑制算法*

王桂胜 ，任清华 ，2，徐兵政 ，刘 洋

（1.空军工程大学信息与导航学院，西安 710077；2.中国电子科技集团航天信息应用技术重点实验室，石家庄 050081）

0 引言

变换域通信系统（Transform Domain Communication System，TDCS）是一种典型的战场认知无线电系统，其波形满足军事信息通信抗干扰、抗截获的要求，因此，得到广泛关注［1］。由于TDCS通过频谱感知和门限判决能够有效规避干扰，因此，优化的门限干扰抑制算法能够有效提高TDCS自身的抗干扰性能。

目前，国内外针对门限的干扰抑制算法研究较多，文献［2］研究了常用的固定硬门限干扰抑制算法，原理较为简单，但缺乏环境适应性；文献［3］针对传统的固定门限能量检测算法存在的问题，提出了联合循环平稳特征检测的双门限算法，能够有效改善性能，但算法复杂度较高，不易实现；文献［4］基于误码率与判决门限的关系，通过降低误码率遍历寻找最佳门限，但算法的效率有待提高。

本文针对硬件实现问题，基于干扰提取模块和自适应门限比较器建立干扰抑制系统，完成对干扰信号的提取和门限判决的干扰抑制；针对门限的干扰抑制问题，提出了基于Neyman-Pearson准则的自适应门限算法。仿真表明，本文提出的自适应门限算法能够有效抑制干扰，具有较好的检测性能。

1 干扰抑制系统

TDCS通过对周围电磁环境进行频谱感知，利用门限判决剔除干扰频谱，从而在变换域内构建规避干扰的基函数，实现传输信息的抗干扰。在实现方面，本文基于干扰提取模块和自适应门限比较器建立干扰抑制系统，完成对干扰信号的提取和门限判决。

1.1 干扰信号提取

为抑制TDCS频谱感知结果中的强干扰，首先需要提取干扰信号。由于实际面临的干扰强度将远大于有效信号强度，且干扰的特征和位置等信息未知，本文通过利用硬限幅器抑制微弱的噪声信号和带通滤波器滤除强度不高的有效信号，将硬限幅器和带通滤波器组合形成干扰信号提取模块，从而获取强干扰的信号成分。

图1 干扰提取模块示意图

1.2 干扰抑制系统

通过构建的干扰提取模块可以有效获取干扰信号，并根据提取的干扰信号模型设计合适的自适应门限干扰抑制算法，并构建自适应门限比较器，本文将干扰提取模块和自适应门限比较器组合，从而形成完整的干扰抑制系统。

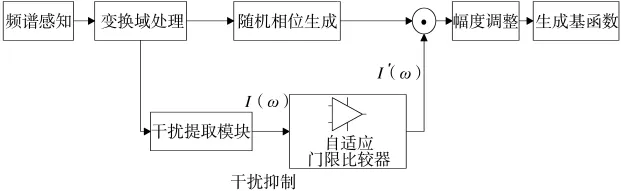
图2 TDCS干扰抑制系统示意图

将干扰提取模块输出的干扰信号作为自适应门限比较器的参考输入信号，干扰抑制的输出信号通过基于干扰抑制算法的自适应门限比较器的输出端产生，从而实现整个系统的干扰抑制作用。

2 基于Neyman-Pearson准则的自适应门限干扰抑制算法

传统的双门限能量检测算法通过利用低门限抑制漏检概率以及高门限降低虚警概率，从而实现干扰的抑制。本文通过采用自适应N-sigma算法确定的初始门限抑制虚警概率，再利用信号统计检测理论中的奈曼-皮尔逊准则确定自适应门限，保证在虚警概率一定的条件下最大化检测概率，从而实现低虚警概率和高检测概率的干扰自适应高效抑制。

2.1 自适应N-sigma算法的初始门限设定

针对TDCS中的干扰抑制问题，通过采用基于Gauss分布理论的N-sigma幅度谱成型算法［5］，调整设定初始门限，能够有效降低漏检概率和虚警概率，提高抗干扰能力。

干扰信号首先进行离散傅里叶变换，得到频谱F（n），再进行计算得到功率谱 R（n），利用得到的均值和方差，根据自适应门限计算公式计算得到Th。具体步骤及相关计算公式如下所示:

Step 1:通过对周围电磁环境进行频谱感知，得到环境自适应因子μ和σ后，根据Gauss分布特性，设定初始门限为:

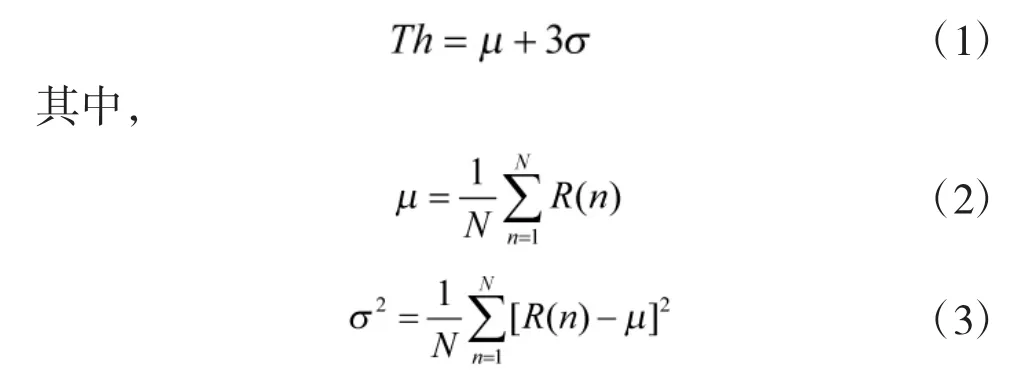
Step 2:根据计算得到的门限Th，与能量检测统计量E（TDCS幅度谱成型过程中采用R（n））比较后形成相应的判决后幅值:

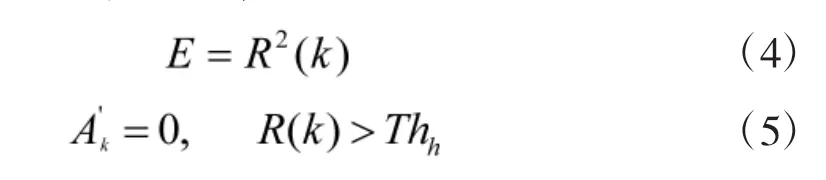
Step 3:在TDCS抑制系统中，根据得到的频谱感知信号，假设H0和H1分别代表无干扰和存在干扰两种状态，将两个假设下的观测信号分别设为:

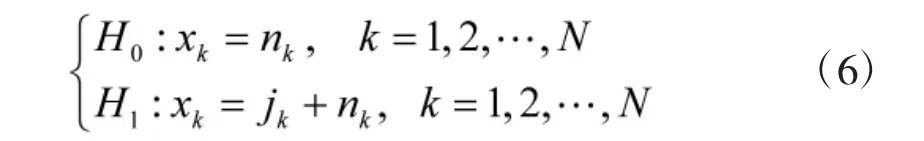
其中，nk表示均值为0、方差为σn2的高斯噪声，jk表示均值为0、方差为σj2的干扰，jk与nk相互统计独立。

Step 4:根据文献［6］，当N较大时，能量检测统计量近似服从Gauss分布，此时TDCS初始门限Th所对应的虚警概率PF为:

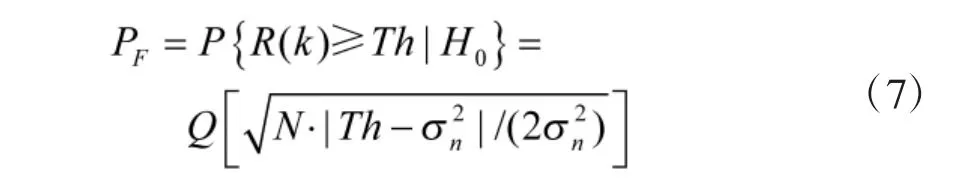
算法描述如下:

算法1

通过设定的初始门限Th可以将干扰的频谱集中特性区分出来，经门限判决确定相应的幅值Ak以及较低的虚警概率PF，并为下一步确定自适应门限提供前提条件。

2.2 基于NP准则的自适应门限设定

为保证TDCS干扰抑制系统能够有效处理频谱感知数据，保留尽可能多的可用频点，避免过多的频谱浪费，提高利用率。本文基于奈曼-皮尔逊（Neyman-Pearson，NP）准则［7］，提出自适应门限算法，保证在虚警概率一定的条件下，最大化检测概率。

假设观测向量x是N维高斯随机向量，故其概率密度函数p（x）取决于x的均值μx和协方差矩阵Cx，其中Cx为等协方差矩阵。

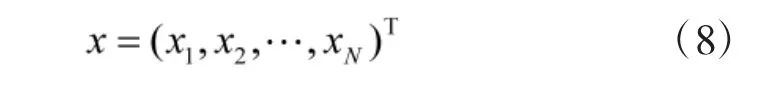
在假设H0下，观测向量x的均值为:

观测向量x的协方差矩阵为:

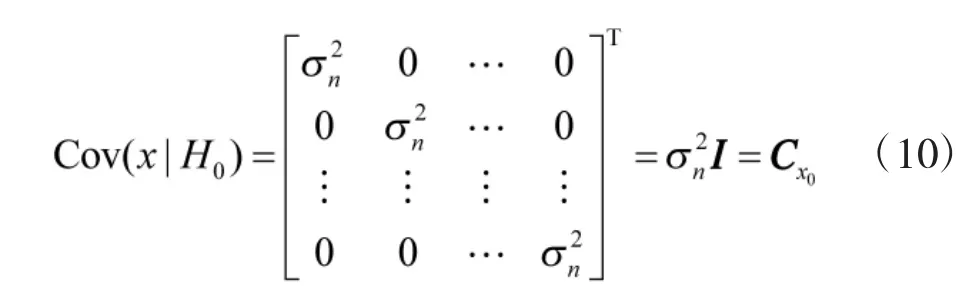
同理可得，在假设H1下:

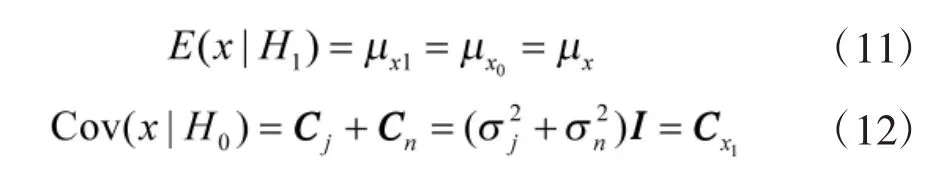
所以，在假设H0和H1下，x的概率密度函数分别为:

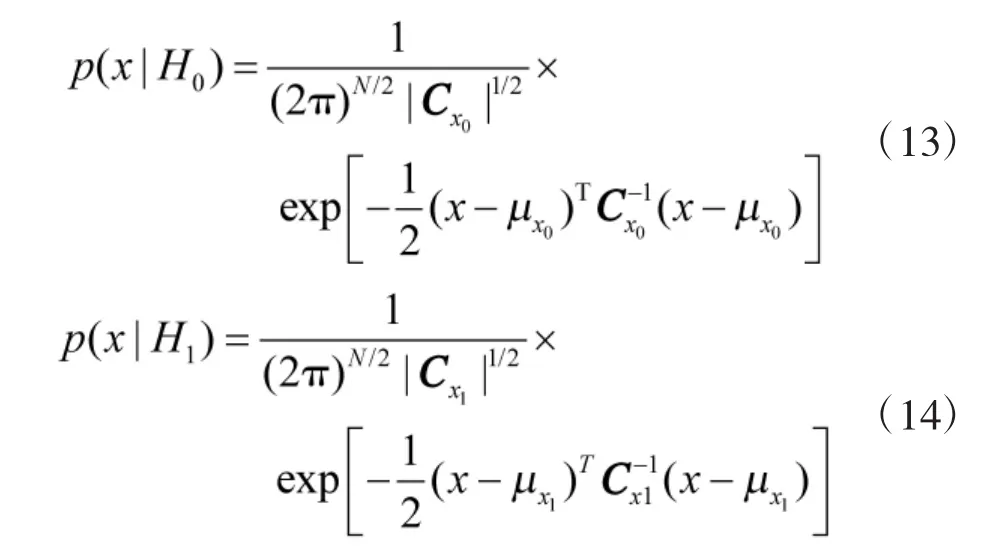
进而将其转换为似然比检验的形式为:

两边取自然对数，化简可得判决表达式:

整理后得:

最终，得到反映检测性能的虚警概率和检测概率分别为:

令M=N/2-1，βF=γ/（2σn2），βD=γ/［2（σj2+σn2）］，在P（H1|H0）较小且βF较大时，通过分部积分法近似处理可得:

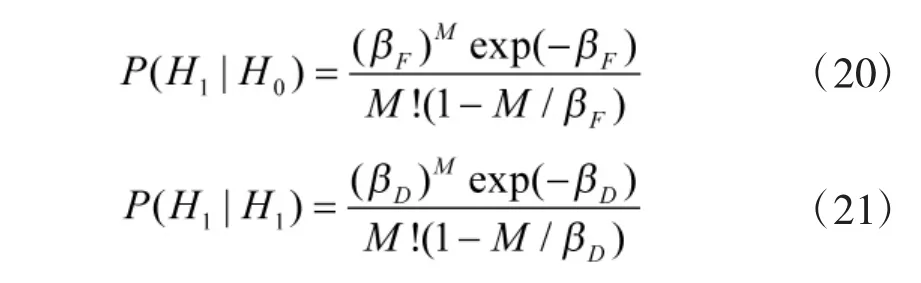
根据离散信号方差与干噪比相关计算公式可得:

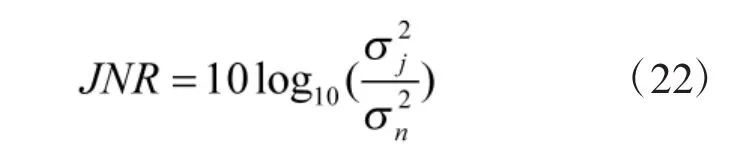
结合已知的虚警概率PF和特定的信噪比下，可得自适应门限及其检测概率PD。当周围电磁环境发生变化时，在虚警概率一定的条件下，条件概率p（x|H1）和p（x|H0）会相应地调整，设定的低检测门限也随之发生变化，因而能有效降低漏检概率，更好地适应TDCS所处的复杂电磁环境。

算法描述如下:

算法2

3 性能分析与仿真验证

3.1 仿真条件的设置

假设信道为高斯白噪声信道，采样频率fs=512Hz，采用m序列生成基函数，调制方式采用CCSK，根据文献［8］分析，将干扰模型参数设定如表1所示。

3.2 干扰抑制效果分析

根据设定的仿真参数，对多音干扰和单分量线性调频干扰分别进行变换域处理，对功率谱均采用自适应门限判决和干扰剔除，为验证本文提出的自适应门限有效性，分别开展下列仿真实验。

表1 实验中使用的干扰模型参数

3.2.1 变换域处理下的噪声影响

由于需要在变换域下处理信号，特别是在门限求解过程中需要对噪声的统计特性进行分析，因此，需要分析在不同干噪比下变换域（特别是分数阶傅里叶变换域）对噪声产生的影响，具体仿真结果如图3所示:

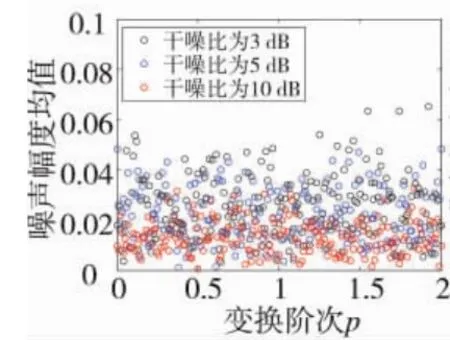
图3 不同变换阶次下的噪声幅度均值分析图

图4 不同变换阶次下的噪声幅度方差分析图

由图3可知，在不同干噪比下，干扰噪声的幅度均值呈现出较大的随机特性，离散效果比较明显，受变换阶次的影响较小，故在本文仿真试验中可忽略变换域阶次变化对噪声幅度均值的影响。

由图4可得，不同干噪比下的噪声幅度方差比较稳定，与干噪比基本呈一定的线性比例关系，在相同干噪比下，噪声的幅度方差基本保持恒定，与变换阶次无关，因此，可将变换域处理下的噪声影响近似视为恒定。

3.2.2 不同门限干扰剔除效果

对比传统硬门限和本文提出的自适应门限，在处理多音干扰时处理效果和判决结果如图5和下页图6所示。

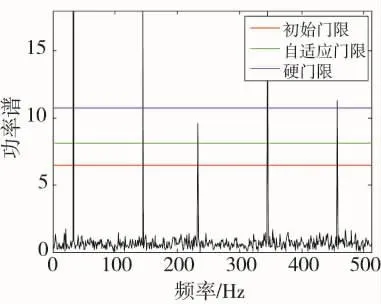
图5 不同门限处理的多音干扰示意图

仿真结果表明，通过采用自适应门限在处理多音干扰较硬门限判决更为准确，不易受部分高强度干扰成分的影响，干扰频点和带宽范围确定基本符合实际参数的设定，干扰抑制效果较好。

如图7所示，进一步对单分量线性调频干扰进行验证，发现本文提出的自适应门限对线性调频干扰的处理同样符合预期的设定。

图6 不同门限处理的多音干扰判决

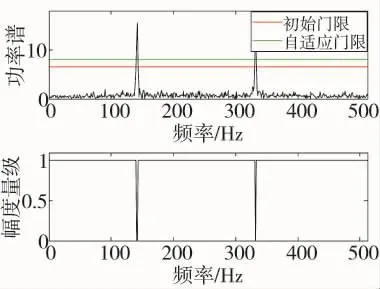
图7 自适应门限处理的线性调频干扰效果示意图

3.3 检测性能分析

在信噪比SNR=-10 dB下，分别以文献［3］提出的门限处理方法和本文提出的自适应门限处理相应的电磁环境，计算相应自适应门限对应下的检测概率、虚警概率和漏检概率，得到其检测性能ROC（Receiver operating characteristics）曲线如图8和图9所示:

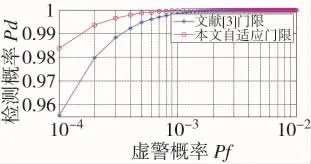
图8 不同门限处理的PD-PF曲线示意图

图9 不同门限处理的PM-PF曲线示意图

由图8、图9可以看出，在信噪比SNR=-10 dB下，检测概率均保持在较高水平，且较文献［3］提高了约3.14%性能增益，虚警概率和漏检概率均保持在较低水平；随着虚警概率的增加，相应的检测概率逐渐增加，漏检概率逐渐下降，能够有效抑制噪声对信号的影响，验证了本文自适应门限具有良好的干扰抑制性能。

4 结论

本文从TDCS面临的干扰门限判决问题出发，基于干扰提取模块和自适应门限比较器建立干扰抑制系统，完成对干扰信号的提取和门限判决的干扰抑制；并提出基于NP准则的自适应门限算法，较传统双门限具有较好的检测性能，但当采集的干扰信号数据量较大时处理耗时较长，检测性能还有待进一步提高。