装甲车辆行进间炮口振动角度误差预测模型*

宋泉良，卢志刚，王 维，方子穆，翟晓燕

（北方自动控制技术研究所，太原 030006）

0 引言

由于路面颠簸、车体底盘振动等原因，装甲车辆在高速机动状态下，其炮口不能在装定的诸元位置处稳定停留；由此，产生了“射击门”的控制思想:当某时刻火炮位置与装定诸元位置之间的夹角在射击门阈值范围内时，才会产生击发信号［1］。现在的火力控制系统在运用射击门控制火炮发射时，仅考虑了火炮的瞬时位置，但是忽略了以下因素:产生击发信号时，虽然火炮位置与射击诸元位置的夹角小于射击门阈值，但是在点火到弹丸出膛的射击延时过程中，火炮仍处于振动状态，弹丸出膛时刻的火炮位置和装定诸元位置的夹角可能超出阈值范围，并且火炮振动速度也将在弹丸出炮口时赋予其切向速度，造成弹道偏离规定的射击位置［2］。因此，对炮口振动的角度误差进行预测成为了研究的重点。其中，预测时间应为射击延时时间，它的大小与弹种有关，但都在10 ms左右，一般情况下可视为常值。

当前常用的预测方法有时间序列方法、神经网络模型、马尔可夫预测法和灰色系统理论等。灰色系统理论的最大优势在于对样本数量较少的序列能够进行准确预测。GM（1，1）模型是灰色系统理论中应用最为广泛的一种预测模型，其基本思想是对原始序列进行累加生成，进而发现其指数规律；然后，利用最小二乘法解得模型中的参数值；最后，建立指数拟合模型进行预测。为了提高GM（1，1）模型的预测精度，许多学者提出了一些改进模型的方法。文献［3］根据新信息优先原理提出了以为初始条件的 GM（1，1）模型；文献［4］中取初值为的加权组合值；文献［5］提出以作为初始值，即预测公式为:·根据对已有数据的拟合精度，从1，2，…，n 中选择。文献［6］证明了背景值对 GM（1，1）模型预测精度的影响；文献［7］提出了利用数值积分中的Newton-Cores公式和插值来重构GM（1，1）模型中的背景值；文献［8］将实际曲线在对应区间上的面积作为背景值，其计算公式为:

为了能够准确预测炮口振动角度误差的变化，本文提出了一种优化GM（1，1）模型。首先，对原始序列进行预处理，使其变换为适用于GM（1，1）模型建模的数据序列；然后，基于误差最小化对传统模型的初始值进行了优化；最后，根据GM（1，1）模型时间响应函数的形式对传统模型的背景值进行了重构。通过实例分析，验证了优化模型具有较高的拟合和预测精度，对炮口振动角度误差变化趋势的判断也更为准确。

1 数据预处理

由于装甲火炮振动的随机性，利用目标跟踪器与镜炮角度传感器获取的火炮相对目标的振动角度误差数据呈现非单调性，通常情况下为振荡序列。GM（1，1）模型适合处理具有非负性、单调性、光滑性的数据序列，但并不适用于炮口振动角度误差这种具有非单调性数据序列的预测。因此，本文在基于短暂射击延时过程中炮口振动角度误差变化平稳的假定下，借助以下方法对原始数据序列进行预处理，使新的数据序列满足GM（1，1）模型的建模需求。

1.1 数据变换

加速平移变换可以将非线性数据序列转换为单调递增序列，能够解决炮口振动角度误差数据的非单调性问题；加权均值变换可以在不破坏原序列单调性的基础上，降低序列的随机性，提高序列的光滑性［9-10］。本文对炮口振动角度误差数据的预处理采用了加速平移变换和加权均值变换相结合的方法。

1.2 序列光滑度检验

定义 1.1［11］若数据序列则称为序列X的光滑比。

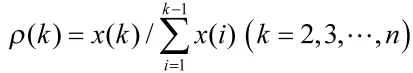
定理1［13］对于任一个非负的、具有准光滑性的序列，其经过一次累加，可得到具有准指数规律的序列。

由定理1可知，当经过加速平移变换、加权均值变换后的序列满足准光滑性时，才可适用于灰色模型。否则，仍需要对数据序列进行光滑性的处理。

2 优化GM（1，1）预测模型的建立

2.1 传统GM（1，1）的建模过程

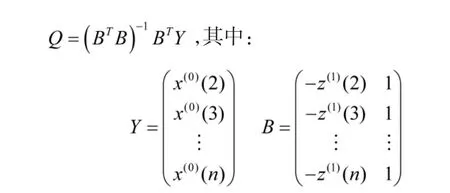
利用上述求得的参数列Q建立相应的白化微分方程:

2.2 初始值的改进

传统GM（1，1）模型是借助最小二乘法的基本思想得到一条拟合曲线，但第1个数据所对应的点并不一定在这条曲线上，同时也无法证明为最优初始条件。本文在文献［5］的基础上提出了一个初始条件的修正式:，其中m在1，2，…，n中选择，βm为与m相关的待定参数，通过选择m和βm的取值，以提高传统GM（1，1）模型的拟合和预测精度。

将初始条件的修正式代入式（6）、式（7），可得到新的序列的预测公式:

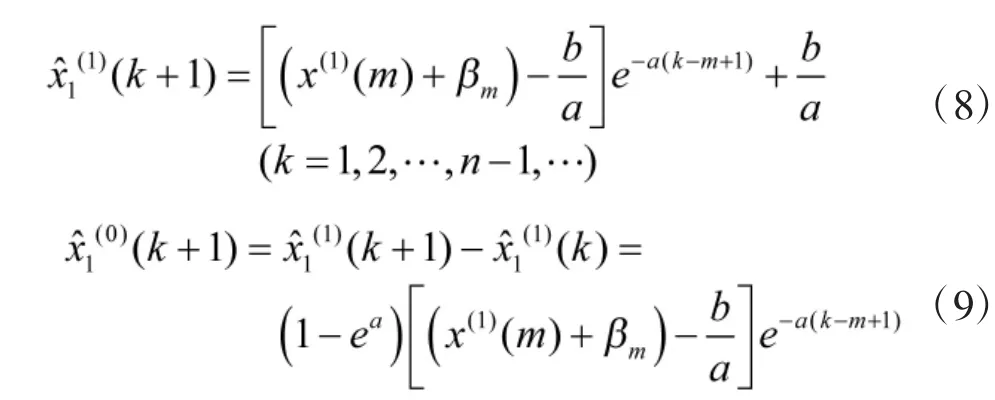
本文利用最小二乘估计的基本思想来确定m和βm的取值，从而使GM（1，1）预测模型的误差最小。利用GM（1，1）模型得到的拟合数据和原始数据，计算得到两者差的平方和，记作Errorm:

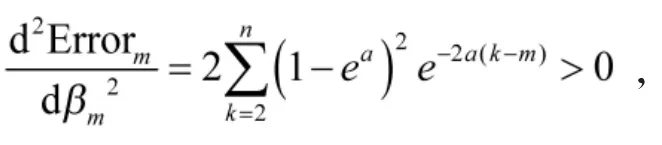
综上，初始条件的修正式为:

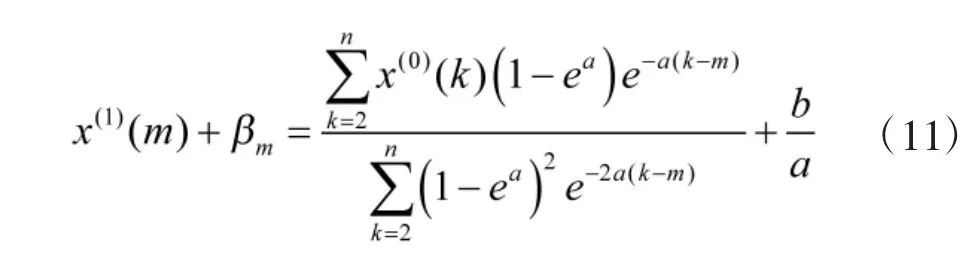
取 m 分别为 1，2，…，n，可得到相应的 βm、Errorm和新初始值，通过比较 Errorm（m=1，2，…，n）的大小，其最小值对应的新初始值即为所求。

2.3 背景值的优化

结合文献［8］中背景值的计算方法，对式（5）两边在区间［k-1，k］上同时积分可得:

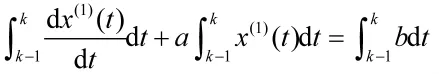
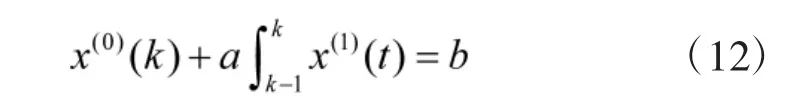
将式（12）与式（4）比较可知，式（12）的积分部分即为背景值。传统GM（1，1）模型中的背景值用的均值生成序列表示，它是一种平滑生成方法。当数据序列变化平缓时，模型的拟合和预测误差较小。但当数据序列变化急剧时，会造成较大的滞后误差，从而影响灰色模型的预测精度。本文将结合灰色微分方程的时间响应函数，直接计算式（12）中的积分部分，达到重构背景值的目的。

由式（7）易知:

2.4 优化GM（1，1）模型的建模步骤

4）利用重构的背景值和式（4）对灰色微分方程的参数进行求解；

6）对上一步的结果进行一次累减生成、加权均值逆变换、加速平移逆变换、平移逆变换得到的预测公式。

3 实例分析

为了验证优化GM（1，1）模型具有较高的拟合和预测精度，下面将以处理的某装甲车行进间火炮高低向炮口振动角度误差的仿真数据作为数据源，其采样间隔时间为10 ms，优化模型的应用过程为:以当前时刻的数据和此前的4个数据作为原始序列，来预测10 ms后的第6个数据，将原始序列的拟合值和第6个数据的预测值与相应的实际值进行比较，检测优化模型的拟合及预测精度。本文的预测过程将在以计算速度较快的DSP作为CPU的控制盒中进行，能够满足实时预测的要求。

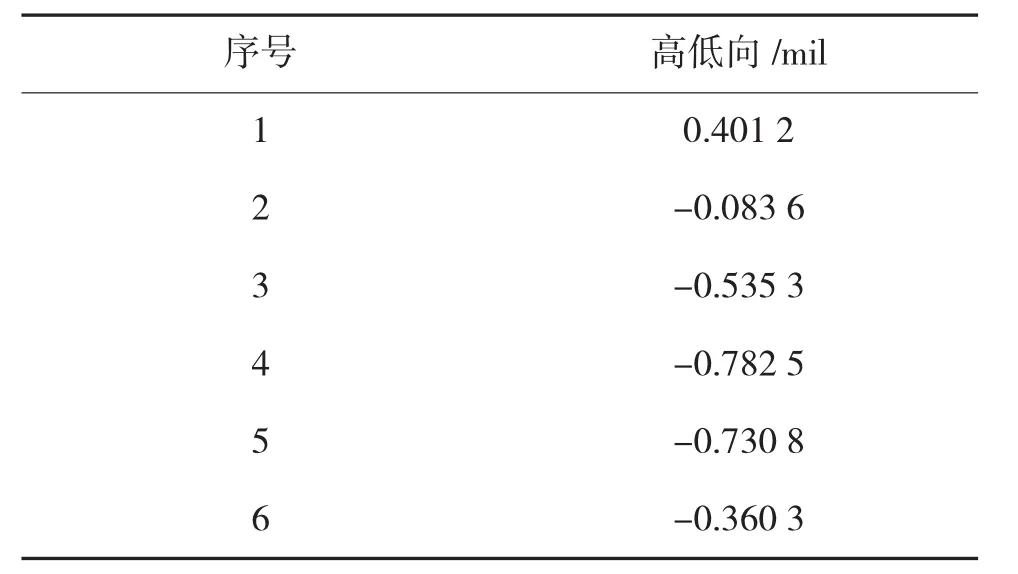
表1 炮口振动角度误差数据

book=124,ebook=127以表1中炮口高低向的振动角度误差数据为例，将其前5个数据作为原始序列经平移变换、加速平移变换和加权均值变换得到数据序列

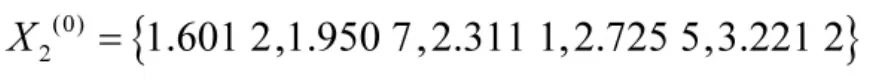
为了与优化GM（1，1）模型进行对比，下面将原始数据序列分别按照传统 GM（1，1）模型、文献［5］中改进初始值模型和文献［8］中改进背景值模型的建模步骤进行数据处理，结果见表3。下页图1为炮口方位向振动角度误差数据的模拟结果。

通过表3可知，经改进的3个模型的拟合、预测精度均高于传统模型，其中优化GM（1，1）模型模拟预测结果的相对误差和为19.40%，平均相对误差为3.88%，处理效果均优于传统模型、改进初始值模型和改进背景值模型。由图1可知，优化GM（1，1）模型的模拟精度较传统模型有了明显的提高。因此，优化GM（1，1）模型能够较好地反映数据的变化趋势，有助于对装甲火炮炮口振动角度误差的预测。

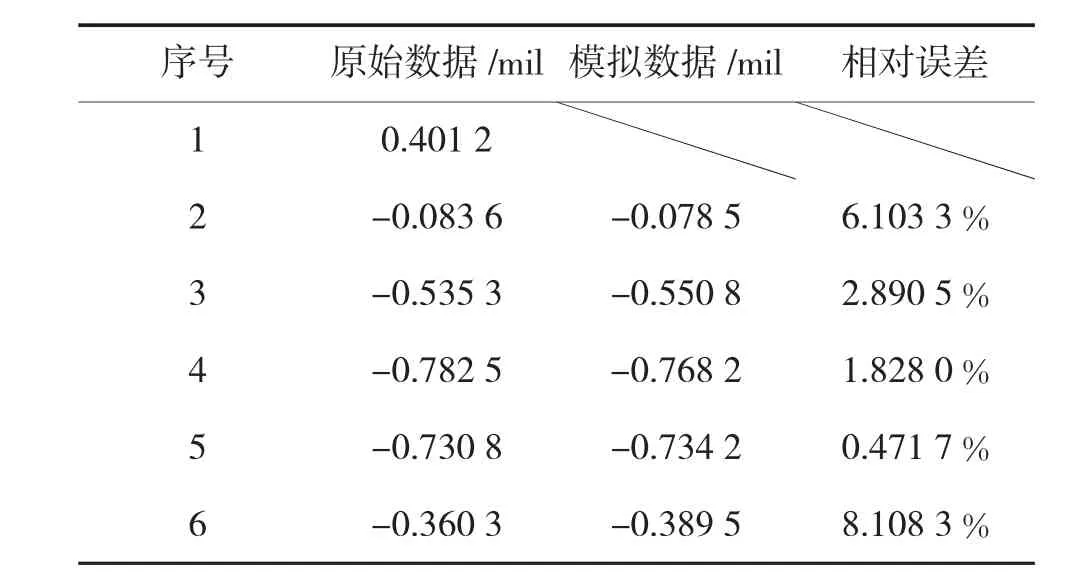
表2 优化模型的拟合及预测结果

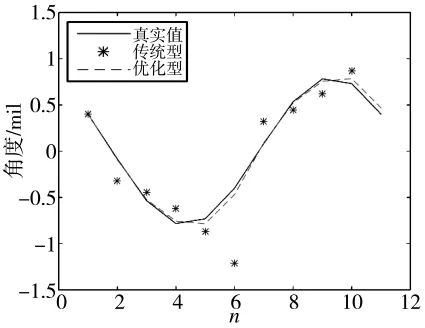
图1 炮口方位向振动角度误差的拟合及预测结果

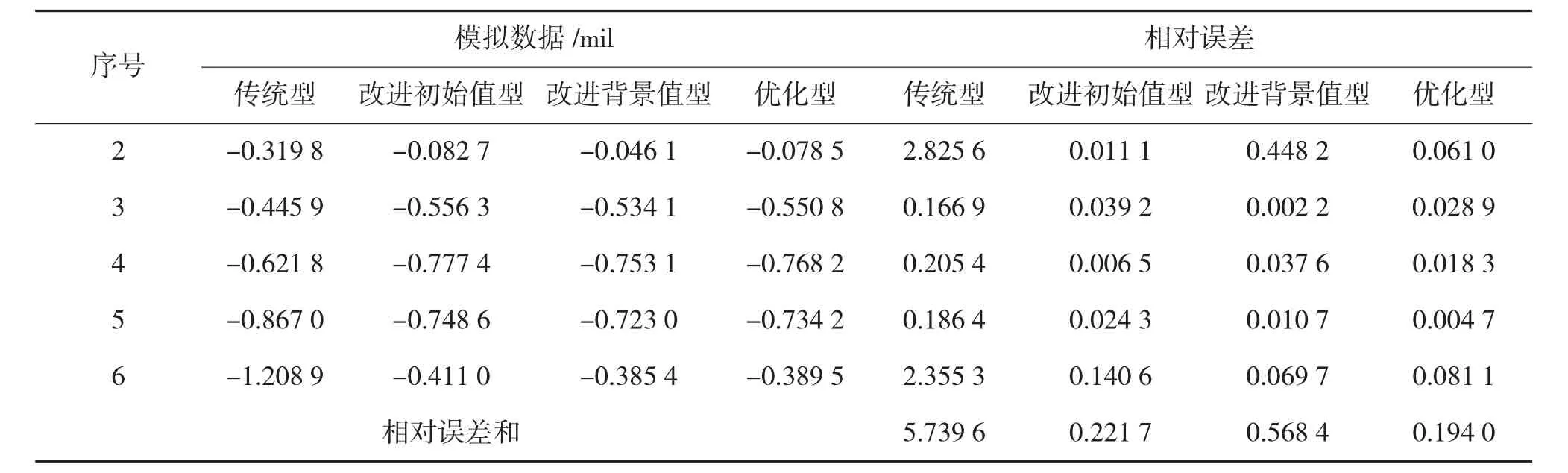
表3 4种模型的模拟结果

4 结论

由于受多种因素的影响，装甲火炮炮口振动角度误差数据具有非线性、随机性强的特点。因此，GM（1，1）模型无法对炮口振动角度误差数据进行直接预测。本文通过对原始数据进行预处理、对传统模型的初始值和背景值进行改进，提出了一种适用于炮口振动角度误差预测的优化GM（1，1）模型。通过对高低向、方位向两组数据处理结果的分析，优化GM（1，1）模型模拟预测结果的平均相对误差分别为3.88%、5.74%，优于传统模型、改进初值模型和改进背景值模型，能够较好地判断炮口振动角度误差的变化情况，为利用其进行智能射击门控制解决装甲火控系统的射击延时误差奠定了基础。