中学数学中的解题教学及案例分析

☉江苏省常州市武进区礼河实验学校 万伟东

中学数学中的解题教学及案例分析

☉江苏省常州市武进区礼河实验学校 万伟东

“问题是数学的心脏”，解题是数学教学的核心，对学生而言，学数学最直接、最显著的表现就是做数学题.数学解题过程是个体思维能力作用于数学活动的心理过程，是一种思维活动，解题切入点不同，运用思维方法不同，体现出来的思维水平也不同.培养数学解题能力，事实上要靠学生自己去经历的一个实践、感悟、内化的过程，数学解题过程大致包括审题、解题计划的制定、解题结构的优化、解答的表达和解题后的反思等环节.数学解题能力的培养也可以根据这些环节进行.下面就这些环节谈谈自己的一些见解和看法.

一、寻求解题途径

有目的地进行各种组合的试验，尽可能将习题化为已知类型，选择最优解法，选择解题方案，经检验后作修正，最后确定解题计划.

（一）理解题意、广泛联想，培养学生思维的广阔性

例1 已知如图1所示的五角星形ABCDE.

求证：∠A+∠B+∠C+∠D+∠E=180°.

在学生充分发表看法的基础上，可对解题思路作以下归纳.

1.考虑到角的和是180°的有关定理，可作以下尝试：（1）互补；（2） 同旁内角互补；（3）三角形的内角和定理.针对这一问题应该从何下手？

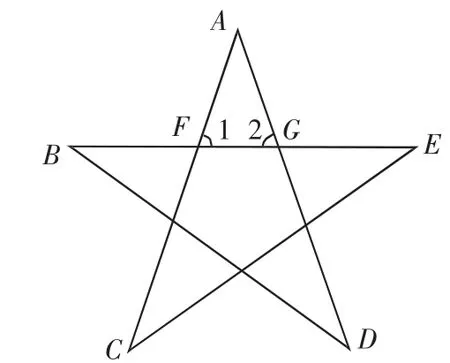
图1

2.要证明五个角的度数和等于180°，联系三角形内角和定理，可考虑将其转化为三角形内角，从而达到目的.通过观察图形，由△BGD和△EFC，联想到三角形的外角定理，得∠1=∠C+∠E，∠2=∠B+∠D，又在△AFG中运用三角形内角和定理，可达到目的.

3.联想到三角形内角和定理，多边形外角和定理以及多边形内角和定理.

（二）重视一题多解，培养学生思维的广阔性、深刻性，从而提高学生的发散思维能力

数学课程标准指出：“要从数学的多角度去分析问题、解决问题，以提高学生的说理论证水平.”根据这一要求，要引导学生多进行对题目的全方位思考的专题讨论，实践证明，这对开发智力、启迪学生思维、提高学生逻辑推理能力大有裨益.

例2 如图2，OA、OB是⊙O半径，OA⊥OB，P是OA上任一点，BP延长线交⊙O于Q，过Q作⊙O的切线，交OA延长线于R，求证：RP=RQ.

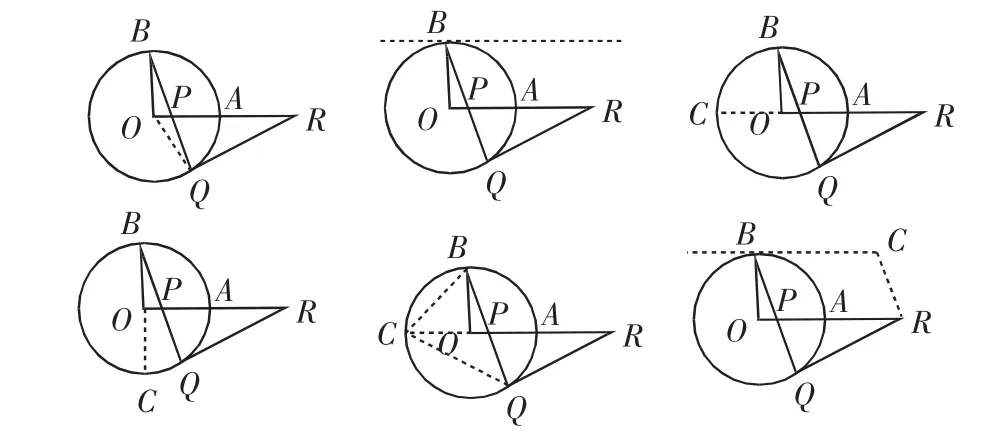
图2

分析：解题的关键是运用等角来证等边.

分析一：连OQ；

分析二：过点B作⊙O的切线；

分析三：延长AO交⊙O于C；

分析四：延长BO交⊙O于C，连CQ；

分析五：延长AO交⊙O于C，连BC、CQ；

分析六：过R作RC∥BQ交⊙O切线BC于C点.

以上六种方法是从不同点出发作辅助线，但都是围绕一个目的，构造基本图形，不过有些图形直观、熟悉，有些隐蔽、陌生，用的知识点少一些.所以对同一问题的角度进行观察、思考、联想，从而可得到不同的解题方法，再对各解法加以比较，找出较好的解法，可以培养学生思维的变通性、流畅性和独特性，从而提高学生学习的积极性.

（三）重视变式训练，培养学生思维的活跃性，从而提高解题能力

变式教学是对数学中的定理和问题进行不同角度、不同层次、不同情形、不同背景的变式，从而暴露问题本质的特点，提示不同知识点的联系.通过变式教学，使一题多用，多题组合，给人以新鲜感，唤起学生的好奇心和求知欲，激发学生的创新精神，拓展他们的创新思维.

例3 如图3，PA为⊙O切线，A为切点，PCB是⊙O割线，

求证：（1）△PAC∽△PBA.（2）PA2=PC·PB.

变式1：基本图形不变，当

PCB过圆心O时，新的结论是：△BAC为直角三角形.如图4（2）.

变式2：此基本图形不变，添∠BAC平分线AM交BP于D，则有结论：PA=PD.如图4（1）.

变式3：此基本图形不变，增添∠APB的平分线，交AB、AC于F、E，则有结论：（1）AE=AF.（2）△AEP∽△BFP.（3）△PCE∽△PAF.如图4（3）.

变式4：此基本图形不变，同时增添∠BAC、∠APB平分线，AM、PF，则有结论：（1）AM⊥PF.（2）FN=NE.（3）AN=ND.如图4（4）.

图3

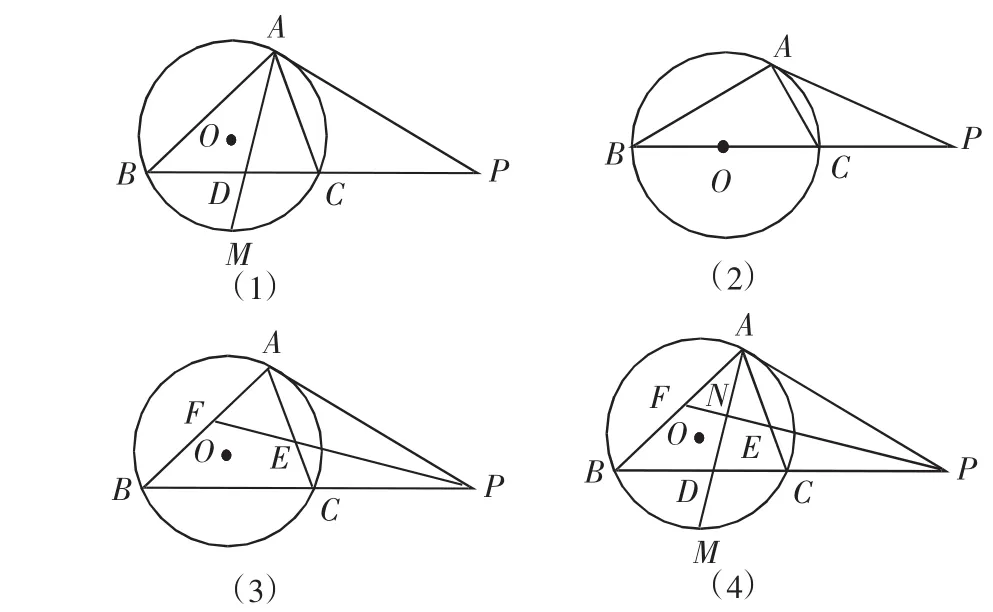
图4

在课本例题、习题的基础上，通过变式题对学生进行训练，使学生掌握变式题与原题的内在联系以及本质，达到一把钥匙开多把锁的效果，这不仅能培养学生善于发现问题、分析问题和解决问题的能力，而且能培养学生的创新思维能力，拓展他们思维空间.

二、解后反思

长期的学习经验表明，不少同学在完成作业或进行解题训练的过程中，普遍欠缺一个提高解题能力的重要环节，就是解题后的反思.一道数学题经过反复思考，苦思冥想解出答案之后，就心满意足了，而不再去思考、探索.这道题考查了我们哪些方面的概念、知识和能力？解答的每一步推理是否合理？这道题有没有其他的解法？多种方法中哪一种比较简单？把这道题的条件或结论进一步推广又会如何？等等.

为了帮助学生养成解题后反思的这种良好的学习习惯，提高解题技巧，在教学时，可选择一些多种解法的习题，给学生训练.

例4 已知：如图5，AB切⊙O于点B，BC⊥AO.求证：∠CBD＝∠ABD.

这道题可以引导学生添加辅助线，有四种证法（证明过程从略）.

图5

证法一：如图5（1），延长AO交⊙O于点E，并连EB，则∠ABD＝∠DEB，∠DBE＝90°.

证法二：如图5（2），过D作⊙O的切线DE交AB于E，则DE⊥AO，∠ABD＝∠BDE.

证法三：如图5（3），延长BC交⊙O于点E，并连ED，则∠ABD＝∠DEB，由垂径定理可得∠CBD＝∠DEB.

证法四：如图5（4），连BO并延长BO交⊙O于点E，连DE，则∠ABD＝∠DEB＝∠EDO，∠EDB＝90°.

提高学生的数学解题能力是一项重要而艰巨的任务，但不能急于求成，不能盲目地搞题海战术.习题的训练要有针对性，讲求质量，讲求效益.在平时的数学教学中，教师应多引导学生进行思考，逐步使学生的思维能力由单向性发展为多向性，让学生在解题过程中获得乐趣、产生灵感、悟出解题的正确思路和方法.

1.董开福.中学数学教材分析.昆明：云南教育出版社，1999.

2.张一民.中学数学教法研究.昆明：云南教育出版社，2001.

3.广西教育学院教研室，广西师范大学数学系，编.讲解·阅读·练习·讨论——中学数学特级教师章保罗教学经验.南宁：广西人民出版社，1984.