浅谈二次函数图像问题的处理

☉江苏省宝应县城北初级中学 沈洪华

浅谈二次函数图像问题的处理

☉江苏省宝应县城北初级中学 沈洪华

二次函数问题是初中数学的重点内容，也是高考的必考点.解决此类问题时，如果能引入函数的图像，常可使解题事半功倍.下面就此类问题中图像的运用提出几点建议，以期对同学们有所帮助.

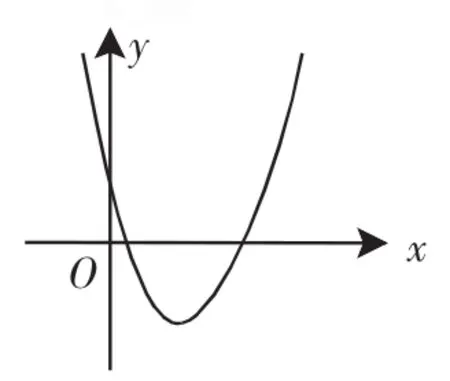
图1

一、识图

例1 二次函数y=a（x+m）2+n的图像如图1所示，则一次函数y=mx+n的图像经过（ ）.

A.第一、二、三象限 B.第一、二、四象限

C.第二、三、四象限 D.第一、三、四象限

解析：因为抛物线的顶点在第四象限，所以－m＞0，n＜0，所以m＜0，即一次函数y=mx+n的图像经过二、三、四象限，故选C.

例2 已知二次函数y=ax2+bx+c的图像如图2所示，那么一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图像大致是图3中的（ ）.

图2

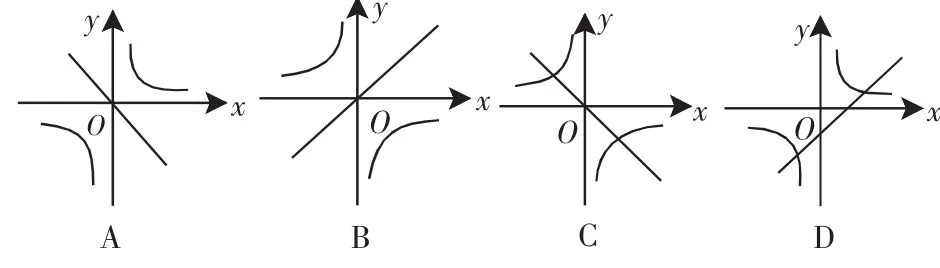
图3

解析：因二次函数图像开口向下，所以a＜0.

因二次函数图像经过坐标原点，所以c=0.所以一次函数y=bx+c过第二四象限且经过原点，反比例函数y=位于第二四象限，纵观各选项，故选C.

点评：解题中做好“识图“，不仅要熟练二次函数图像，还要熟练如一次函数的图像、反比例函数的图像等.

二、用图

例3 二次函数y=ax2+bx的图像如图4所示，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为（ ）.

A.－3 B.3 C.－6 D.9

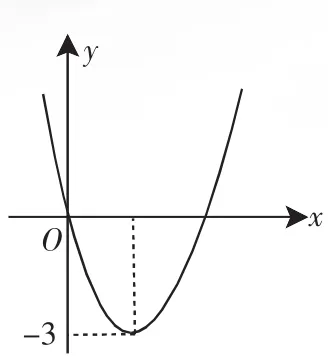
图4

又一元二次方程ax2+bx+m=0有实数根，所以△=b2－4am≥0，即12a－4am≥0，即12－4m≥0，解得m≤3，故m的最大值为3.

故选B.

点评：本题实际考查了抛物线与x轴的交点问题，解题中如能运用好已知中所给的函数图像，则可使解题思路顺利形成.

三、构图

例4 设A（－2，y1），B（1，y2），C（2，y3）是抛物线y=－（x+1）2+a上的三点，则y1，y2，y3的大小关系为（ ）.

A.y1＞y2＞y3B.y1＞y3＞y2

C.y3＞y2＞y1D.y3＞y1＞y2

解析：因函数的解析式是y=－（x+1）2+a，如图5，知对称轴是x=－1，所以点A关于对称轴的点A′是（0，y1）.

那么点A′、B、C都在对称轴的右边，而对称轴右边y随x的增大而减小，于是y1＞y2＞y3.故选A.

点评：本题主要考查了二次函数图像上点的坐标特征.应准确构造出二次函数图像，心中有图，解题就不会碰壁.

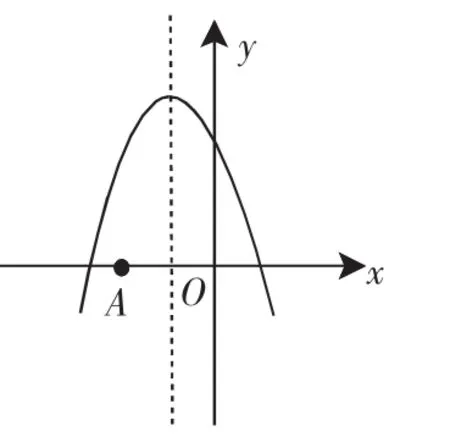
图5

四、变图

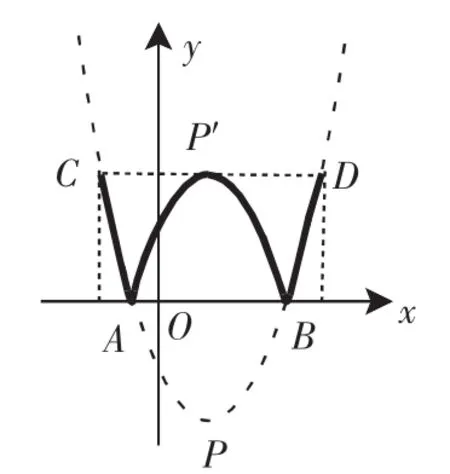
图6

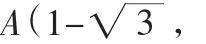
（1）求原抛物线的解析式；

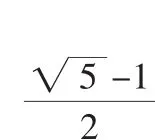
分析：（1）利用P与P′（1，3）关于x轴对称，得出P点坐标，利用待定系数法求出二次函数的解析式即可.

（2）根据已知得出C、D两点坐标，进而得出“W”图案的高与宽（CD）的比.

解：（1）因为P与P′（1，3）关于x轴对称，

所以P点坐标为（1，-3）.

点评：此题主要考查了待定系数法求二次函数的解析式以及二次函数的应用，根据已知得出C、D两点坐标是解题的关键．