解析初中数学中分式方程的解法及应用

☉江苏省扬州市江都区实验初级中学 姚永华

解析初中数学中分式方程的解法及应用

☉江苏省扬州市江都区实验初级中学 姚永华

分式方程的解法及应用是中考考查的重点内容，考查时大多以直接解分式方程和列分式方程解应用题的形式出现.因此，对本部分知识需要进行专项训练，熟练掌握解分式方程的方法，并通过应用题使学生进一步使用代数中的方程去反映现实世界中的等量关系，体会代数方法的优越性，进一步培养学生化实际问题为数学问题的能力和分析问题解决问题的能力.下面就对分式方程的解法及其应用做具体解析.

一、分式方程的有关概念

分式方程是方程中的一种，且分母里含有未知数的（有理）方程叫做分式方程.

二、分式方程的解法

解分式方程的基本思路是将分式方程化为整式方程，具体做法是“去分母”，即方程两边同乘最简公分母，这也是解分式方程的一般思路和做法.

1.去分母

方程两边同时乘以最简公分母（最简公分母：①系数取最小公倍数②出现的字母取最高次幂③出现的因式取最高次幂），将分式方程化为整式方程；若遇到互为相反数时.不要忘了改变符号.

2.解整式方程

移项，若有括号应去括号，注意变号，合并同类项，把系数化为1求出未知数的值；

3.验根

求出未知数的值后必须验根，因为在把分式方程化为整式方程的过程中，扩大了未知数的取值范围，可能产生增根.验根时把整式方程的根代入最简公分母，如果最简公分母等于0，这个根就是增根.否则这个根就是原分式方程的根.若解出的根是增根，则原方程无解.如果分式本身约分了，也要带进去检验.一般的，解分式方程时，去分母后所得整式方程的解有可能使原方程中分母为零，因此要将整式方程的解代入最简公分母，如果最简公分母的值不为零，则是方程的解.

（1）注意去分母时，不要漏乘整式项.（2）増根是分式方程去分母后化成的整式方程的根，但不是原分式方程的解.（3）増根使最简分母等于0.

三、分式方程的应用

列分式方程解应用题的一般步骤是：找等量关系—设—列—解—检验—答.

例1 玉树地震后，有一段公路急需抢修，此项工程原计划由甲工程队独立完成，需要20天，在甲工程队施工4天后，为了加快工程进度，又调来乙工程队与甲工程队共同施工，结果比原计划提前10天，为抗震救灾赢得了宝贵时间，求乙工程队独立完成这项工程需要多少天？

考点：分式方程的应用．专题：工程问题．分析：等量关系为：甲工作量+乙工作量=1．

解析：设乙工程队独立完成这项工程需要x天．

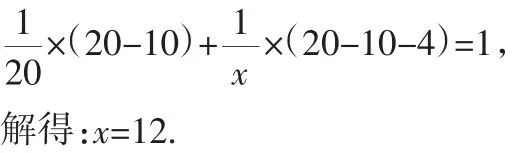
经检验x=12是原方程的解．

答：乙工程队独立完成这项工程需要12天．

点评：工作量问题常用的等量关系为：工作量之和为1，易错点是准确找到各个队的工作时间．

例2 某公司开发生产的1200件新产品需要精加工后才能投放市场，现有甲、乙两个工厂都想加工这批产品．公司派出相关人员分别到这两间工厂了解生产情况，获得如下信息：

信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；

信息二：乙工厂每天比甲工厂多加工20件．

根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品.

考点：分式方程的应用．

分析：总工作量除以所用时间即为工效，而乙工厂每天比甲工厂多加工20件的前提下，甲工厂单独完成比乙工厂单独完成多用10天，据此可列方程．

解：设甲工厂每天能加工x件新产品，则乙工厂每天能加工（x+20）件新产品．

经检验：x=40是所列方程的解．

乙工厂每天加工零件为：x+20=60．

答：甲工厂每天能加工40件新产品，乙工厂每天能加工60件新产品．

点评：理解题意找出题中的等量关系，列出方程，注意分式方程一定要验根．

例3 在某道路拓宽改造工程中，一工程队承担了24千米的任务.为了减少施工带来的影响，在确保工程质量的前提下，实际施工速度是原计划的1.2倍，结果提前20天完成了任务，求原计划平均每天改造道路多少千米.

解析：该题目的等量关系是计划用的天数-实际用的天数=20天

设原计划平均每天改造道路x千米，根据题意，得：

解这个方程，得x=0.2.

经检验，x=0.2是原方程的解.

答：原计划平均每天改造道路0.2千米.

例4 杭州国际动漫节开幕前，某动漫公司预测某种动漫玩具能够畅销，就用32 000元购进了一批这种玩具，上市后很快脱销，动漫公司又用68 000元购进第二批这种玩具，所购数量是第一批购进数量的2倍，但每套进价多了10元.求：

（1）该动漫公司两次共购进这种玩具多少套？

（2）如果这两批玩具每套的售价相同，且全部售完后总利润率不低于20%，那么每套售价至少是多少元？

解：（1）设动漫公司第一次购进x套玩具，由题意得：

经检验，x=200是所列方程的根.

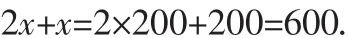
所以动漫公司两次共购进这种玩具600套.

（2）设每套玩具的售价为y元，由题意得：

解分式方程作为基础性知识，在中考中以直接考查为主，也经常与数轴等知识综合考查，解决问题时要注意分式方程根的检验是必不可少的步骤.列分式方程解应用题，在中考中多以解答题为主，有时也会出现在选择题或填空题中，解决此类题目的关键是准确理解题意，确定题目中的等量关系，列出分式方程.而在解此时的分式方程时，不仅要检验所得解的是否满足方程式，还要检验是否符合题意.