如何在解题中运用分类讨论思想

☉江苏省兴化市唐刘学校 王长平

如何在解题中运用分类讨论思想

☉江苏省兴化市唐刘学校 王长平

数学思想是数学知识、数学技能、数学方法的本质体现，是形成数学能力，数学意识的桥梁.因而在《课标》中，数学思想被视为数学基础的重要组成部分，而分类讨论思想是十分重要的数学思想.

分类讨论思想逻辑性强，它不仅用于数学解题，而且在其他领域也有广泛的应用.通过数学中的分类解题，可以增强分类的意识，拓宽解题的空间，培养全面解决问题的能力.

近年来，在中考或数学竞赛中，经常出现多解问题，不少学生往往不注意这一点，很容易导致漏解，使答案不完整.为了保证求得的答案正确、合理，应正确应用分类思想指导解题.

一、根据定义确定多解

例1 解方程|2x+5|=3.

解：根据绝对值定义，将它分解为两个方程来解：

①当2x≥－5时，2x+5=3，所以x=－1；

②当2x＜－5时，2x+5=－3，所以x=－4.

所以，原方程的解是：x1=－1，x2=－4.

二、根据图形的特征确定多解

例2 △ABC中，已知AB=AC，且过△ABC某一顶点的直线可将△ABC分成两个等腰三角形，试求△ABC各内角的度数.

分析：由对称性知，可先分直线过A，B两点的两种情况，在这两种情况下又需按腰分类，也有两种情况，故有四解.

解：（1）如图1，过A作直线AD交BC于D，有AD=DB=DC，此时△ABC的各角为45°，45°，90°.

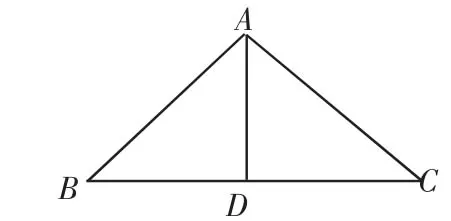
图1

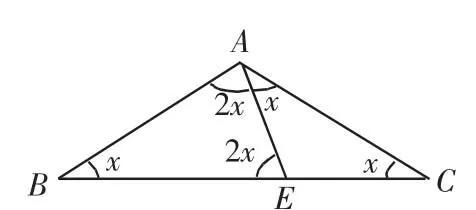
图2

（2）如图2，过A作直线AE交BC于E，有BE=AB，CE=AE，设∠C=∠B=∠CAE=x°，则∠BAE=∠BEA=2x°，由x+2x+x+x=180，得x=36，此时△ABC的各个内角为36°，36°，108°.

（3）如图3，过B点的直线BF交AC于F，BF=BC=FA，设∠A=∠ABF=x°，则∠C=∠CFB=2x°，∠CBF=x°，由x+2x+2x=180，得x=36，此时△ABC各内角为36°，72°，72°.

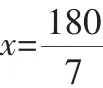
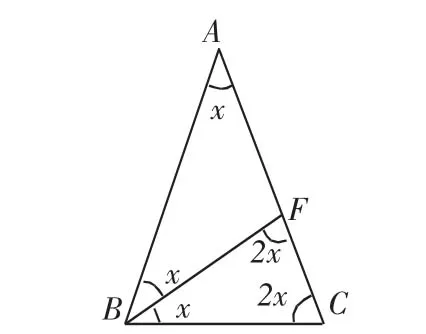
图3

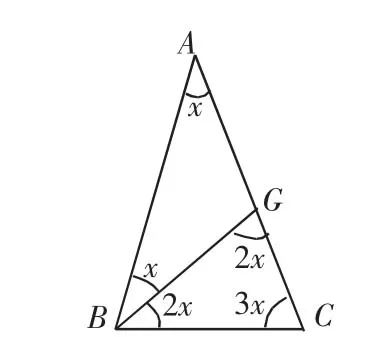
图4

三、根据对称性确定多解

例3 以线段AB为直径作一个半圆，圆心为O，C是半圆上的点，且OC2=AC·BC，求∠CAB.

解：（1）当点C与A同在四分之一的圆上时，如图5，过C作CD⊥AB于D.因为AB为半圆的直径，所以∠ACB=90°，所以AC·BC=AB·CD=2OC·CD.而OC2=AC·BC，所以2OC·CD=OC2，所以CD=OC，所以∠COD=30°.又因为△BOC是等腰三角形，所以

图5

图6

四、根据位置关系确定多解

例4 ⊙O1和⊙O2相交于A，B两点，公共弦AB与连心线O1O2交于G，若AB=48，⊙O1和⊙O2的半径分别为30和40，求△AO1O2的面积.

（2）当圆心在公共弦的同侧时，如图8.同法求得S△AO1G=216，S△AO2G=384，类似于（1）求得S△AO1O2=S△AO2G－S△AO1G=384－216=168.

图7

图8

由上可见，在数学问题的解决过程中，我们要正确运用分类讨论这一数学思想方法，同时也要挖掘其中的隐含条件，恰当地运用整体、数形结合等数学思想，避免一些不必要的分类讨论.