初中数学动点最值问题的探讨
江苏省淮阴中学 朱翠英
最值问题是初中数学中一类综合性很强的问题,是初中数学教学中的一个重要组成部分,在整个初中数学的学习中都存在最值问题,这类试题也是近几年中考的热点问题之一,它主要考查学生对平时所学的内容综合运用,突出了对学生数学素质的考查.通过这类试题的教学,可以培养学生的探究能力和创新意识,培养学生运用所学数学知识解决实际问题的能力,对学生思维能力的提高有较大的帮助.
解这类题目要尽可能简便地建立坐标系,再写出各点坐标,设出动点坐标,或是运用数形结合思想,把代数式转化为几何图形,或是结合动点运动属性,分析图形特征,根据题目的条件写出关系式,最后求解.本文试从以下几个方面对这类问题作一些简单的探讨.
一、出现一个动点的解题方法
这类试题的解决方法主要是通过轴对称,将动点所在直线同侧的两个定点中的其中一个,映射到直线的另一侧,当动点在这个定点的对称点及另一定点的线段上时,由“两点之间线段最短”可知线段和的最小值,最小值为定点线段的长.
例1 如图1,已知L是一条乡村公路,A、B为公路一侧的两个村庄,为方便学生上学,准备在公路边上新建一所小学,如果是请你设计新学校的校址,你准备选在哪里可使学校两村庄到学校的距离和最小?
解析:作B关于L的对称点B′,有MB=MB,于是MA+MB=MA+MB′≥AB(当且仅当从运动到AB′和L的交点M′时等号成立),建在M′点符合条件.

图1
二、出现两个动点的解题方法
两动点,其中一个随另一个动(一个主动,一个从动),并且两动点间的距离保持不变.用平移方法,可把两动点变成一个动点,转化为“两个定点和一个动点”类型来解.
例2 如图2,河岸两侧有A、B两个村庄,为了村民出行方便,计划在河上修一座桥,桥修在何处才能使两村村民来往路程最短?

图2
解析:设桥端两动点为M、N,那么N点随M点而动,MN等于河宽,且MN垂直于河岸.将B向上平移河宽长到B′,线段AB′与河北岸线的交点即为桥端M点位置.四边形BB′MN为平行四边形,B′M=BN,此时AM+BN=AM+B′M=AB′值最小.那么A、B两村来往最短路程为:AM+MN+NB=AB′+MN.
三、出现三个动点的解题方法
当题中出现三个动点时,在求解时应注意两点,(1)作定点关于动点所在直线的对称点.(2)同时要考虑点点、点线、线线之间的最短问题.
例3 如图3,在菱形ABCD中,AB=2,∠BAD=60°,E,F,P分别为AB,BC,AC上动点,求PE+PF最小值.
解析:作E关于AC所直线的对称点E′,于是有PE+PF=PF+PE′≥E′F,又因为E在AB上运动,故当E′F和AD,BC垂直时,E0F最短,易求E0F=x+y=4.
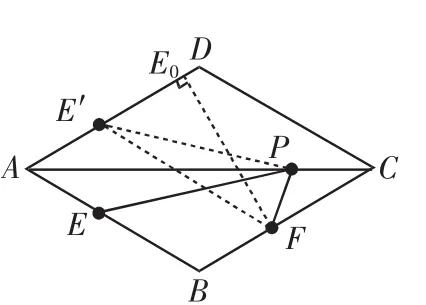
图3
四、动点最值在求代数最值问题中的应用
在数学教学中,注重对学生数形结合思想的引导和启发,有助于学生在解决问题时从不同角度去思考和探索,从多角度去解决问题,对培养学生的转化能力也有很大的帮助.
解析:可以让学生思考直角三角形中直角边和斜边的边长关系,就能想到是以x、1为直角边的直角三角形斜边的长是以y、2为直角边的直角三角形斜边的长,那么这个问题就可转化成求两条线段和的最值问题.这种解决问题的思维方法只有在长期的训练中逐渐养成,是一个渐进的过程,不可操之过急.
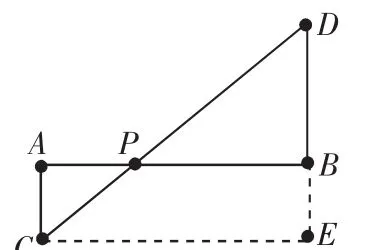
图4
如图4,AB=4,P为AB上一动点. 设PA=x,PB=y.CA⊥AB,DB⊥AB,A、B为垂足,且CA=1,BD=2,则PC+PD=可知当点P,C,D在同一条直线上时,PC+PD最小.作CE垂直DB的延长线交点为E,所以,EC=4,ED=2+1=3,即:PC+PD=DC=,故最小值为5.
五、动点最值在圆中的运用
对于圆上有动点的几何最值问题,常需根据动点运动属性,分析图形特征,运用直径是圆中最大的弦或不等量公理求解.
例5 如图5,已知AB是半圆的直径,如果这个半圆是一块铁皮,四边形ABDC是内接半圆的梯形,试问:怎样剪这个梯形,才能使梯形ABDC的周长最大?
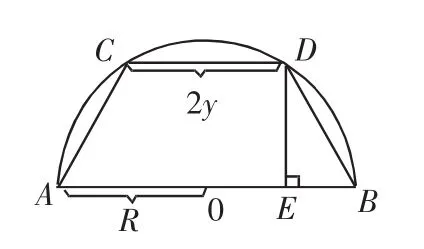
图5
解析:本例是求半圆AB的内接梯形的最大周长,可设半圆半径为R.由于AB∥CD,必有AC=BD.
若设CD=2y,AC=x,那么只需求梯形ABDC的半周长u=x+y+R的最大值即可.
总之,解决这一类动点最值问题,关键在于善于作定点关于动点所在直线的对称点,或动点关于动点所在直线的对称点,运用数形结合思想,这对于解决动点最值问题有着事半功倍的作用.

