因式分解总复习

☉海南华侨初级中学 王明照

因式分解的基本方法有提公因式法，公式法，分组分解法，十字相乘法及其他方法；因式分解的步骤常常用口诀表述为“一提二套三分组四其他”，也就是说，先看是否有公因式，再看能否套公式，若所给式子有四、五项的就要分组，这些方法都无法解决就要采用一些特殊技巧如添项、分拆、重组等.还常常要进行一些恰当的变形，使多项式达到分解要求.本文围绕2011年全国各个省市考试题为例介绍一下这些常见的因式分解方法及小技巧.需要说明的是，要想熟练掌握这些基础知识和技巧，还需要同学们通过平时练习去体验我们所讲的方法和技巧.

一、因式分解的概念

把一个多项式化成几个整式积的形式叫做把这个多项式因式分解，也叫做把这个多项式分解因式.因式分解是整式乘法的逆向变形.

注意：（1）分解因式要分解到不能分解为止；（2）结果中有相同因式时要写成幂的形式.

二、因式分解的方法

1.提公因式法：多项式=公因式×（原多项式除以公因式所得的商）.

提公因式法的步骤：

第一步：正确找出公因式（①多项式各项系数都是整数时，公因式的系数是各系数的最大公约数；②字母取各项的相同的字母；③相同字母的指数取最低次数）.

第二步：提出公因式并确定另一个因式，将结果写成积的形式.

2.运用公式法：把乘法公式反过来，就可以把多项式分解因式.这种分解因式的方法叫做运用公式法.

（1）平方差公式a2-b2=（a+b）（a-b）

公式特点：左边是二项式，是两个数的平方差，右边是这两个数的和与差的积.

（2）完全平方公式a2±2ab+b2=（a±b）2

公式特点：左边是三项式，是两个数的平方和与这两个数的积的两倍的和或差；右边是这两个数的和或差的平方.

注意：①完全平方公式中，中间项是两个数的积的2倍，其符号决定是和的平方还是差的平方.

②公式中的两个数可以是单项式，也可以是多项式.

3.十字相乘法：x2+（p+q）x+pq=x2+px+qx+pq=（x2+px）+（qx+pq）=x（x+p）+q（x+p）=（x+p）（x+q）.

所以x2+（p+q）x+pq=（x+p）（x+q）.关键要根据一次项系数把常数项分解.

4.分组分解法：把多项式进行适当的分组，分组后能够有公因式或运用公式，这样的因式分解方法叫做分组分解法.

分组的原则——有公因式提取或可运用公式.

分组分解的目的是最终达到整体多项式因式分解，要求分组后可直接提取公因式或可直接运用公式，但必须使各组之间能提公因式或运用公式继续分解.

应注意：

（1）要注意分解因式的对象是整式，不是整式不能分解因式.

（2）不要因式分解后又乘回来.

（3）注意分解一定要彻底.

（4）因式分解的结果是几个因式的积，而不是把多项式其中某几项化为积的形式.

（5）因式分解的结果能写成幂的形式就应写成幂的形式.

三、典型例题

类型一：考查因式分解的定义.

例1（辽宁鞍山3分）下列因式分解正确的是______.

A.x3-x＝x（x2-1） B.x2＋3x＋2＝x（x＋3）＋2

C.x2-y2＝（x-y）2D.x2＋2x＋1＝（x＋1）2

答案：D.

考点：因式分解的定义，平方差公式.

分析：把一个多项式化为几个最简整式的积的形式，这种变形叫做把这个多项式因式分解.注意三原则：分解要彻底，最后结果只有小括号，最后结果中多项式首项系数为正.据此有：

A.x3-x＝x（x2-1），分解不彻底，选项错误；B.x2＋3x＋2＝x（x＋3）＋2，不符合结果为最简整式的积的定义，选项错误；C.x2-y2＝（xy）2，平方差公式应用错误，选项错误；D.x2＋2x＋1＝（x＋1）2，选项正确.故选D.

类型二：考查运用提公因式法因式分解.

例2 （广西来宾3分）分解因式：1-x2=______.

答案：（1+x）（1-x）.

分析：因式1-x2中，可知是二项式，没有公因式，直接用平方差公式分解即可：1-x2=（1+x）（1-x）.

例3 （重庆江津4分）分解因式：2x3-x2=______.

答案：x2（2x-1）.

分析：观察等式的右边，提取公因式x2即可求得答案.

类型三：考查运用平方差公式因式分解.

例4 （海南3分）分解因式x2-4=______.

答案：（x+2）（x-2）.

分析：利用平方差公式直接分解：x2-4=（x+2）（x-2）.

例5（湖南怀化3分）因式分解：a2-9=______

答案：（a+3）（a-3）.

分析：利用平方差公式直接分解：a2-9=（a+3）（a-3）.

类型四：考查运用完全平方公式对多项式进行因式分解.

例6 （山东济南3分）分解因式：a2-6a+9＝______.

答案：（a-3）2.

分析：本题是一个二次三项式，且a2和9分别是a和3的平方，6a是它们二者积的两倍，符合完全平方公式的结构特点，因此用完全平方公式进行因式分解：a2-6a+9=（a-3）2.

例7 （山东威海3分）分解因式：16-8（x-y）＋（x-y）2=______.

答案：（x-y-4）2.

考点：完全平方公式，代数式代换.

分析：因为16-8m＋m2=（m-4）2，所以令m=x-y得16-8（x-y）＋（x-y）2=（x-y-4）2.

类型五：综合运用提公因式以及平方差公式进行因式分解.

例8 （广西玉林、防城港3分）分解因式：9a-a3=______.

答案：a（3+a）（3-a）.

分析：根据提取公因式法和应用公式法分解因式：9a-a3=a（9-a2）=a（3+a）（3-a）.

例9 （江苏南通3分）分解因式：3m（2x-y）2-3mn2＝______.

答案：3m（2x-y+n）（2x-y-n）.

分析：3m（2x-y）2-3mn2=3m［（2x-y）2-n2］=3m（2x-y+n）（2xy-n）.

例10 （山东莱芜4分）分解因式：（a+b）3-4（a+b）=______.

答案：（a+b）（a+b+2）（a+b-2）.

分析：（a+b）3-4（a+b）=（a+b）［（a+b）2-4］=（a+b）（a+b+2）（a+b-2）

类型六：综合运用提公因式以及完全平方公式进行因式分解.

例11 （江苏扬州3分）因式分解：x3-4x2+4x=______.

答案：x（x-2）2.

分析：应用提取公因式法和应用公式法因式分解：x3-4x2+4x=x（x2-4x+4）=x（x-2）2.

例12 （山东东营4分）分解因式：x2y-2xy+y=______.

答案：y（x-1）2.

分析：x2y-2xy+y=y（x2-2x+1）=y（x-1）2.

例13 因式分解：3a+12a2+12a3=______.

答案：3a（1+2a）2.

分析：先提取公因式3a，再根据完全平方公式进行二次分解：

3a+12a2+12a3=3a（1+4a+4a2）=3a（1+2a）2.

类型七：综合运用平方差公式以及完全平方公式进行因式分解.

例14 （湖南岳阳3分）分解因式：a4-1=______.

答案：（a2+1）（a+1）（a-1）.

分析：运用平方差公式进行两次分解即可：a4-1=（a2+1）（a2-1）=（a2+1）（a+1）（a-1）.

类型八：运用分组分解法进行因式分解.

例15 （山东潍坊3分）分解因式：a3+a2-a-1=______.

答案：（a+1）2（a-1）.

考点：分组分解法因式分解，提取公因式，平方差公式.

分析：当被分解的式子是四项时，应考虑运用分组分解法进行分解.本题应采用两两分组，然后提取公因式（a-1）得a3+a2-a-1=a2（a+1）-（a+1）=（a+1）（a2-1）=（a+1）2（a-1）.

例16（四川遂宁4分）阅读下列文字与例题：

将一个多项式分组后，可提公因式或运用公式继续分解的方法是分组分解法.

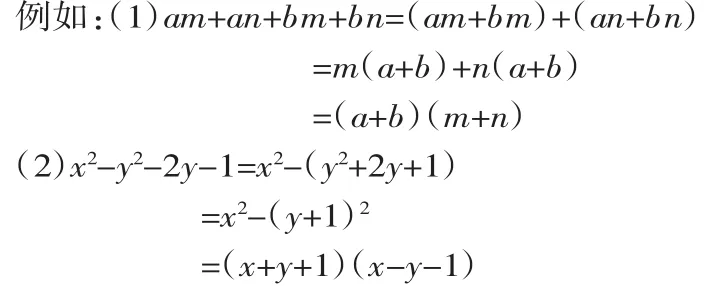
试用上述方法分解因式a2+2ab+ac+bc+b2=______.

答案：（a+b）（a+b+c）.

分 析 ：a2+2ab+ac+bc+b2=a2+2ab+b2+ac+bc=（a+b）2+c（a+b）=（a+b）（a+b+c）.

类型九：运用十字相乘法因式分解.

例17 （贵州黔东南4分）分解因式：x2-2x-8=______.

答案：（x+2）（x-4）.

分析：根据一次项系数为-2，所以-8分解为2和-4相乘，x2可分解为两个x相乘，交叉乘后一相加刚好是-2x，所以根据十字相乘法可分解为（x+2）（x-4）.

也可以利用配方法把这个多项式配成两个式子的平方之差的形式，然后利用平方差公式因式分解.

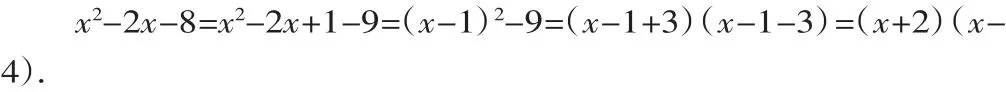
类型十：求代数式的值.

例18 （甘肃天水4分）若x＋y=3，xy=1，则x2＋y2=______.

答案：7.

考点：求代数式的值，完全平方公式.

分析：将所求的式子配成完全平方公式，然后将x+y和xy的值整体代入求解：

类型十一：综合题.

例19 （广东广州10分）分解因式：8（x2-2y2）-x（7x＋y）＋xy.

答案：原式＝8x2-16y2-7x2-xy＋xy＝x2-16y2＝（x＋4y）（x-4y）.

考点：整式的混合运算，运用公式法因式分解.

分析：首先利用多项式乘以多项式法则进行化简，正好符合平方差公式，再运用公式法分解因式即可解答.

练习题：

1.（m+n）（x-y）+（m-n）（y-x）

2.4x2-12xy+9y2

3.x4-y4

4.a（a+2）+b（b+2）+2ab

5.x2+4x-12

6.（x+1）（x+2）（x+3）（x+4）+1

点评：因式分解在各省市中考试卷中大多数是选择、填空题，十字相乘法和分组分解法考得比较少，主要以提公因式法和公式法的综合运用为主，所以在复习时应重点练习用这三种方法.