运用建模思想揭示数学本质

☉江苏省姜堰市第四中学 颜小兵

所谓模型化思想，就是把所考查的实际问题转化为数学问题，构造相应的数学模型，通过对模型的研究，使实际问题得以解决的数学思想方法.下面仅以模型化思想在锐角三角函数中的应用为例，加以说明.

同学们在学习了解锐角三角函数的应用后，接触到了几类应用问题，诸如，测量问题（测高度距离等）航海问题等.这些问题的背景千变万化，如能将这些实际问题通过建立数学模型，寻求其本质上的同一性.既可以揭示这些应用问题的数学本质，又能使自己从题海中解脱出来，实现以不变应万变.

在锐角三角函数的应用中测量问题题型种类较多，如测量校园内某一旗杆的高度，测量某一建筑物或山坡的高度.在海上测量某灯塔目标或船与测量人的距离等，其实，这些问题归纳起来无外乎下列两类.

第一类：异侧测量——观测点在被测物体的异侧

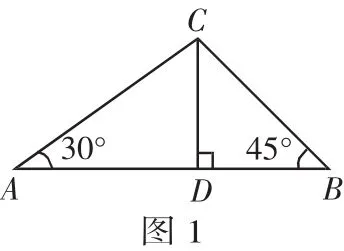
例1 某旅游景点有一古塔CD甲、乙两人分别站在塔的西、东两侧的A、B处，测得塔顶的仰角分别为30°和45°（如图）已知A、B间距离为60m，求塔的高度.（结果保留根号）

分析：本题已知AB=60m，若设塔高CD=xm，则可设法利用三角函数将AD、BD，表示出来，代入AD+BD=AB即可.

点评：本例中利用已知两角分别为30°和45°的△ABC和AB边上的高CD，组成的图形作为数学模型，实现了从实际问题向数学问题的转化.

例2 某船在海面上正以20海里每小时的速度向正东方向航行，在A处，测得灯塔C在北偏东60°方向，行驶3小时后到B处，测得灯塔C在船的西北方向，已知灯塔C的周围20海里范围内有暗礁，问船在航行过程中有无触礁危险.

分析：本题与例1看似两个不同类的问题，先构建数学模型（如图2）.

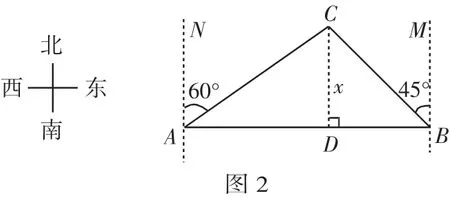
由已知∠CAN=60°，所以∠CAB=30°.

∠CBA=45°，只要求出C到AB的距离CD即可.

不难发现本题与例1只是背景不同，数学模型完全一致，故解题目方法基本相同.

第二类：同侧测量——观测点在被测物体的同侧

例3 小红家住在某高层建筑内，从窗后A处看到前面与该楼同一直线上停着两辆汽车B、C，测得俯角分别为60°和45°，两辆汽车之间的距离测得为15m，求小红家窗户A到地面的距离.（窗本身的高度忽略不计）（结果保留根号）

分析：方法与例1类似、先构建数学教学模型（如图3）.

设窗高AD为xm，只需将BC用x表示出来即可.

解：设AD=xm，依题意得：

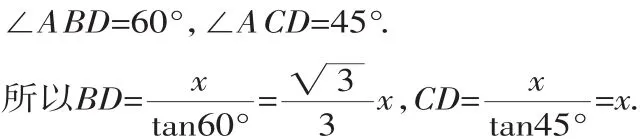
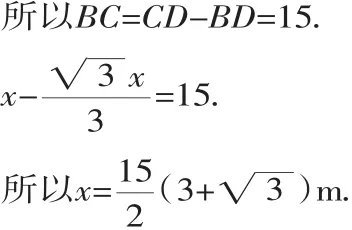
答：（略）

变式一：如图4在地面上相距15米的BC两点，测量某一建筑物，测得仰角分别为45°和60°，求建筑物的高度.

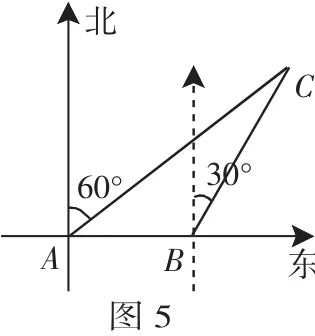
变式二：如图5某船以36海里的速度向正东方向航行，在点A测得某岛C在北偏东60°方向上，航行半小时后可达B点，测得该岛在北偏东30°方向上，已知该岛周围16海里有暗礁（1）试说明点B是否在暗礁区内？（2）若继续向东航行有无触礁危险.

答案：（1）BC=AB=18＞16.

所以点B在暗礁区外.

（2）有触礁危险

通过上面几例分析我们发现，变式一和变式二的数学模型与例3基本一致，有些背景不同的问题，其实构建数学模型是基本一致的.

通过这里所讲的锐角三角函数的应用问题目，希望同学们在今后的学习过程中，只要善于归纳和总结，你一定会发现更多的这样的实例.当我们运用模型化思想建立了合理的数学模型之后，就会发现它们原来有着许多相同或相似之处.