构在抛物线上的最架——两道中考试题及变式研究 值

☉湖北省武汉市吴家山第三中学 吴 波

初中阶段，涉及到“最”值问题的定理、性质有三个：1.两点之间，线段最短，以及其派生出来的三角形两边之和大于第三边，两边之差小于第三边；2.二次函数的最大值和最小值；3.垂线段最短.纵观近年相关中考题，抛物线中的最值问题，大约涉及以下四个方面：线段最长、面积最大、线段之和最小、线段之差最大，前面二者可转化成用“二次函数最值”解决，后二者常用轴对称转化成用“两点之间，线段最短”来解决.本文拟以去年山东两个地方中考题为例，叙述架构在抛物线上的最值问题，及可能的变式.为与本文所述最值相关，故将原题中无关问题舍去.

一、线段最长、面积最大，利用“二次函数的最值”解决

例1（2011山东威海）如图1，抛物线y=ax2+bx+c交x轴于点A（-3，0）和点B（1，0），交y轴于点E（0，-3）.点C是点A关于点B的对称点，直线y=-x+m过点C，交y轴于点D.点K为线段AB上一动点，过点K作x轴的垂线与直线CD交于点H，与抛物线交于点G，求线段HG长度的最大值.

略解：易求抛物线表达式为y=x2+2x-3，直线CD的表达式为y=-x+5.设K点的坐标为（t，0），则H点的坐标为（t，-t+5），G点的坐标为（t，t2+2t-3）.

因为点K为线段AB上一动点，

所以-3≤t≤1.

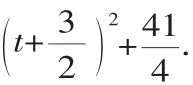
变式2：如图2，点G在何处时，△GDC的面积最大？

分析1：由于CD为定值，所以高GS最大时，面积最大.

分析2：要高GS最大，可平移直线CD，当其与抛物线只有一个交点时，这个交点即为所求点G.

分析3：过C、D两点作GH的垂线段，将△GDC重新分割组合，则有：

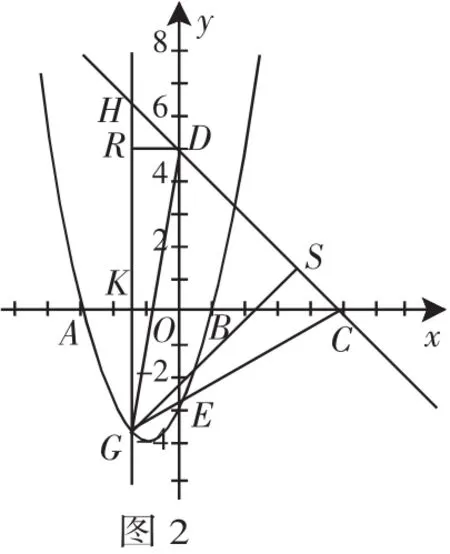
求线段最长和面积最大，关键在于将其表示出来，再用二次函数最值解决.

二、线段之和最小，线段之差最大，利用“三角形两边之和大于第三边，两边之差小于第三边”解决

分析：本题本质即为已知点C、点D在x轴同侧，在x轴上找一点M，使MC＋MD最短.作出点C关于x轴的对称点C′，连接C′D交x轴于点M，根据轴对称性及两点之间线段最短可知，MC＋MD的值最小.求直线C′D的解析式，进而可求点M坐标.

变式1：如图3，在抛物线对称轴上找一点E，使△EAC的周长最小，并求其值及点E的坐标.

分析：使△EAC的周长最小，即AC+CE+EA的值最小，而线段AC长度不变，从而转化成两条线段之和最小.题中易找到点A关于对称轴的对称点B，所以连BC，与对称轴的交点即为所求点E.此时，CE＋EA=CE＋EB=BC.线段AC和BC可用勾股定理求出，从而可求出△EAC的周长最小值.求直线BC的解析式，即可得点E坐标.

变式2：点C关于对称轴的对称点为N，在直线AC上找点P，使四边形BNDP的周长最短，并求点P的坐标.

变式3：如图3，在抛物线对称轴上找一点F，使点F到点B和点C的距离之差最大，并求点F的坐标.

分析：由点A、点B关于对称轴对称，可知FA=FB，要使得FBFC的值最大，即是使得FA-FC的值最大.根据三角形两边之差小于第三边可知，当点A、C、F三点在同一直线上时，其差值最大，所以过点A、C的直线交抛物线对称轴于点F，则该点即为所求.

变式4：如图4，点A关于BC的对称点为N，AG∥BN交直线BC于点G，若点P，点Q为直线BC、BN上的两动点，连NP、PQ、QG，求这三条线段和的最小值.

分析：由点A、N关于直线BC对称可知NP＋PQ的最小值为AQ，而AQ＋QG的最小值，则可找点G关于BN的对称点G′，连AG′，交BC、BN的交点即为所求的P、Q点的位置，最小值为AG′的长，在直角三角形AGG′中用勾股定理可求.

求线段和最小及差最大，题中的抛物线只是一个载体，本质是利用轴对称将多线段转化在一条直线上求最大（小）值的问题.