动静结合演绎精彩
☉浙江省绍兴县平水镇中 冯 雁 沈岳夫
所谓“动静结合”,这里是指在研究的两个几何图形中,一个图形随着两点(一动一定或两个动点)之间线段长度的改变,根据题目条件其生成的图形也随之改变,即称之为“动图”,另一个图形静止不变,即称之为“静图”,两者结合叫动静结合.纵观2011年学业评价考试题,笔者发现这类试题呈上升趋势,它们集几何、代数知识于一体,数形结合,有较强的综合性,题目灵活、多变,动中有静,动静结合,能在动图变化中发展学生的空间想象能力、综合分析能力,特别是注重对分类思想的考查.
解决此类问题的策略是:首先,要注意用运动与变化的眼光去观察和研究图形,把握图形运动与变化的全过程,抓住其中的等量关系和变量关系,并特别关注一些不变量、不变关系或特殊关系,由特殊情形过渡到一般情形;其次,要把握图形在动态中暂时静止的某一瞬间,将这些点锁定在某个位置,并能根据题意依次画出各个不同状态的图形,以及相邻状态的交界处的图形;第三,明确解题方法,当一个问题有确定图形的变量之间的关系时,通常建立函数模型求解;当确定特殊图形的特殊位置关系时,通常建立方程模型求解.在求解过程中要关注图形的生成依赖的“临界点”的变化.现结合2011年的学业考试题,采撷几例予以剖析,以期待读者的重视.
一、因两点间长度发生改变,探究其生成的动圆与静圆的相切问题
例1 (2011年南京市)如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,P为BC的中点.动点Q从点P出发,沿射线PC方向以2cm/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为ts.
(1)当t=1.2时,判断直线AB与⊙P的位置关系,并说明理由.
(2)已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值.
分析:(1)判断直线AB与⊙P的位置关系,即要求圆心P到直线AB的距离与圆半径PQ的关系即可.通过公式可求PQ的长为2.4cm;求圆心P到直线AB的距离就应作辅助线:过点P作PD⊥AB,垂足为D,由△PBD∽△ABC求出,从而得出结论.
(2)对于⊙P与⊙O相切,可能存在两种情况,一是⊙P在⊙O内两圆相切;二是⊙O在⊙P内两圆相切.但都有一个共同点,即两圆的圆心距等于两半径之差,故只要求出圆心距OP和两圆半径即可求得.
解:(1)直线AB与⊙P相切.理由如下:
如图2,过点P作PD⊥AB,垂足为D.在Rt△ABC中,∠ACB=90°,由于AC=6cm,BC=8cm,所以AB=10cm.又P为BC的中点,可知PB=4cm.又∠PDB=∠ACB=90°,∠PBD=∠ABC.所以△PBD∽△ABC.得,解得PD=2.4cm.当t=1.2时,PQ=2t=2.4cm.所以PD=PQ,即圆心P到直线AB的距离等于⊙P的半径.故直线AB与⊙P相切.
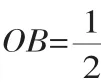
点评:此题是一个单点Q发生变动,从而使以PQ为半径的圆逐渐变大.两圆的位置关系应从内含→内切(⊙P在⊙O内)→相交→内切(⊙O在⊙P内)→内含的五种情况分类讨论.解答此类问题的关键是依题画图,针对所画的图形,借助特殊“临界点”位置(内切)的关系,运用方程思想、数形结合思想、分类讨论的思想解决问题.可见,通过正确画图,搭起了学生思考的“脚手架”.让学生自主探究,不断地深入思考,从而提高了学生分析问题、解决问题的能力,同时也提高了学生的分类意识.
二、因两点间长度发生改变,探究其生成的正三角形与矩形的重叠部分面积

例2 (2011年重庆市)如图3,矩形ABCD中,AB=6,BC=,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速动动,到达A点后,立即以原速度沿AO返回;另一动点F从P点出发,以每秒1个单位长度的速度沿射线PA匀速动动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧,设运动的时间为t秒(t≥0).
(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值.
(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围.
(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.
分析:(1)当边FG恰好经过点C时,∠CFB=60°,BF=3-t,在Rt△CBF中,解直角三角形可求t的值;
(2)按照等边△EFG和矩形ABCD重叠部分的图形特点,分为0≤t<1,1≤t<3,3≤t<4,4≤t<6四种情况,分别写出函数关系式;
(3)存在.当△AOH是等腰三角形时,分为AH=AO=3,HA=HO,OH=OA三种情况,分别画出图形,根据特殊三角形的性质,列方程求t的值.
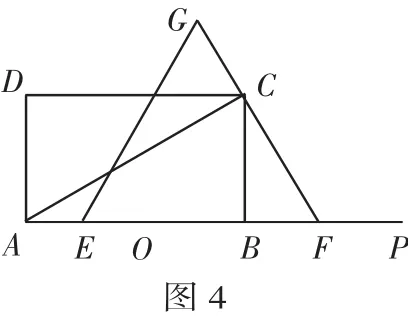

(2)当0≤t<1时,如图5,设EG交CD于点M,过点M作MH⊥AB.在Rt△EMH中,∠MEH=60°,MH=BC=而BE=BO+EO=3+t,所以CM=BH=BE-EH=3+t-2=1+t.进而求得
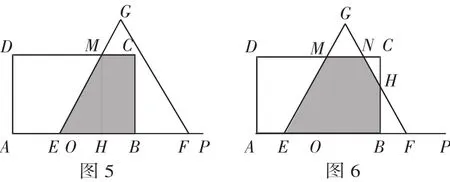
当1≤t<3时,如图6,在Rt△BFH中,∠BFH=60°,BF=3-t,则BH=BF·tan60°=3△BFH∽△CNH,得解得CN=t-1.所以S阴影=S梯形BCME-S△HCN=
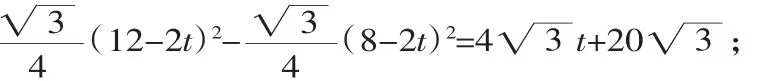
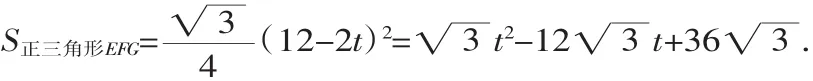
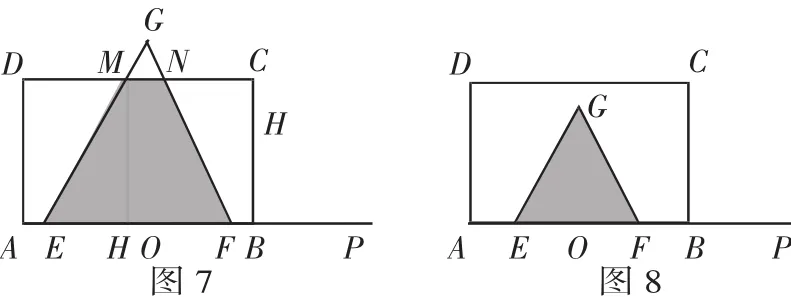
(3)存在,理由如下:

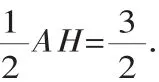



(Ⅱ)当HA=HO时(如图10),则∠HOA=∠HAO=30°,又因为∠HEO=60°,所以∠EHO=90°.进而得EO=2HE=2AE.又AE+EO=3,所以AE+2AE=3,得AE=1.所以3-t=1或t-3=1,解得t=2或4.
(Ⅲ)当OH=OA时(如图11),则∠OHA=∠OAH=30°,所以∠HOB=60°=∠HEB.则点E和O重合,得AE=3.所以3-t=3或t-3=3,解得t=6(舍去)或t=0.
综上所述,存在5个这样的值,使△AOH是等腰三角形,即:
点评:此题设置了两个动点的问题情境,主要考查了等腰三角形、正三角形、相似三角形、矩形、梯形、直角三角形等有关知识,这种集多个知识、多种解题思想于一体的综合题,既能考查学生的创造性思维品质,又能体现学生的实际水平和应变能力.解答此类问题的关键是根据题意,画出符合实际条件的图形,由于线段EF的长度在改变,所以正△EFG与矩形ABCD重叠部分的形状也随之改变,依次为直角梯形、五边形、等腰梯形、正三角形等.然后观察图形,寻找“临界点”(t=0,1,3,4,6),分类分析产生各种情况的图形,以及相邻情况的分界图的生成.因此,在运动中不能被“动”所迷惑,而应在“动”中求“静”,“以静制动”,抓住要害,各个击破,将动态问题转化为静态问题来解决,找出动态过程中的不变量,同时,要注意分类讨论思想的渗透,以及转化思想、函数建模在解题中的灵活运用.
三、因两点间长度发生改变,探究其生成的正方形与三角形的重叠部分的函数最值问题
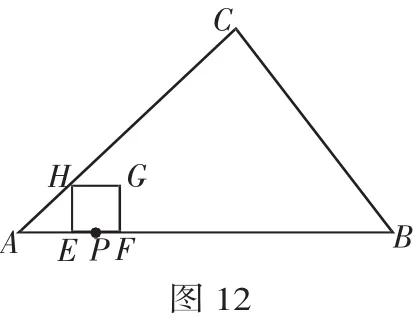
例3(2011年淮安市)如图12,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立即以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧,设E、F运动的时间为t秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
(1)当t=1时,正方形EFGH的边长是________;当t=3时,正方形EFGH的边长是________.
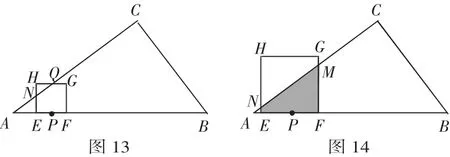
(2)当0<t≤2时,求S与t的函数关系式.
(3)直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少?
分析:(1)当时t=1时,可得EP=1,PF=1,EF=2,即为正方形EFGH的边长为2;当t=3时,PE=1,PF=3,即EF=4.


解:(1)当t=1时,EF=2;当t=3时,EF=4.

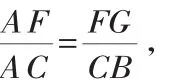

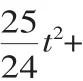
点评:此本题以三角形为载体,由动点产生正方形,在运动过程中,正方形的边长也是一个由变到不变的过程,即在0<t≤2时正方形的边长由短变长,在2<t≤8时正方形的边长是定长4,正方形EFGH与△ABC重叠部分的形状也是一个不断变化的,依次为正方形、五边形、梯形、三角形、梯形、五边形、六边形、四边形等.在变化中隐含着不变的因素,点“动”引起“形”动,这与一般的动态问题的不同.设置简洁、清晰,三个问题层次分明,具有一定的区分度,体现了学业考压轴题的选拔功能.从考查的知识点来看,有正方形、梯形、相似三角形的性质、二次函数,同时解题过程需要用到数形结合、静态到动态、一般到特殊、特殊到一般、分类讨论等多种重要的数学思想和方法,对学生分析问题、解决问题的能力提出了较高的要求.此题是一道不可多得的好题,有利于培养学生的思维能力,但难度较大,具有明显的区分度.

