两种群竞争系统的稳定性及其数值仿真

李晓康

（陕西理工学院 数学系，陕西 汉中 723000）

两种群生态系统包括食饵－捕食者系统、共生系统、竞争系统［1].竞争系统是指两个种群生活在同一环境下，具有相同的食物来源，为了生成而竞争，竞争的常见结局是竞争力较弱的种群数量逐步减少直至灭绝，竞争力较强的种群数量逐步增加趋于环境容许的最大数量［2].对两种群竞争系统的研究，取得了大量的成果，文献［3]对具有捕获两种群竞争系统的捕获系数进行了研究，王庚对两种群竞争非线性反应扩散系统奇摄动Robin问题及其渐进性进行了研究［4－5].文献［6]研究了具有阶段结构的两种群竞争系统的周期解，文献［7－9]研究了具有年龄结构三竞争种群系统的适定性.

本文将对两种群竞争系统Volterra prey－predator模型进行稳定性分析，并对模型进行数值仿真.

1 Volterra prey－predator模型

两竞争种群的数量x，y所满足的微分方程组为

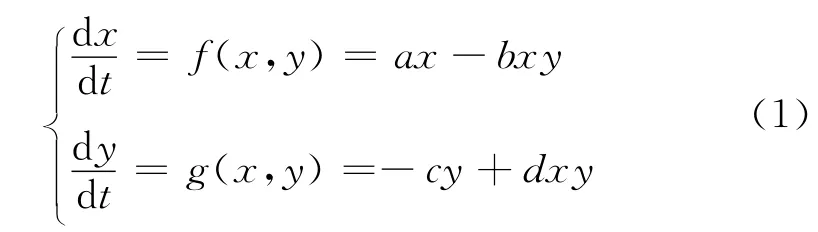
模型（1）的含义为：种群数量变化率与自身数量成正比，同时由于自身数量和竞争者数量的阻滞作用，故在模型中减去它们的交叉项.

由于模型（1）为非线性模型，得不到其解析解，下面通过稳定性及相轨线进行分析.

2 稳定性及相轨线

为分析两种群相互竞争的结果，下面分析模型（1）的平衡点的稳定性.由平衡点的定义，由模型（1），令其右端为0，得方程组：

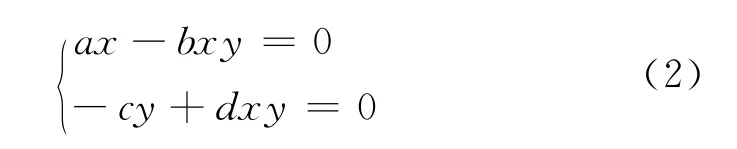
求解方程组（2），可得两个平衡点：P1（0，0），P2平衡点P1（0，0）表明两种群最终消失，平衡点表明两种群最终趋于某稳定数量，这是希望看到的结果.下面分析平衡点稳定的条件.

由平衡点的稳定性理论：

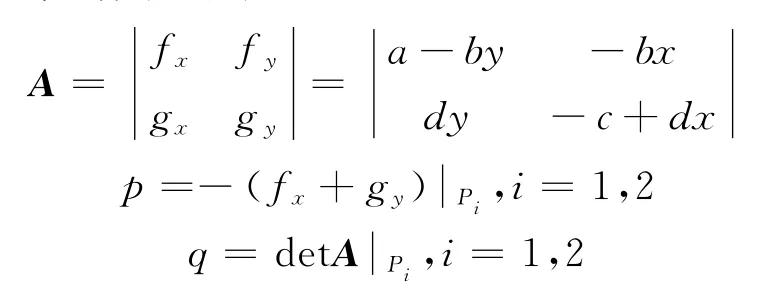
将2个平衡点的p，q计算结果及稳定条件列入表1.

表1 平衡点及其稳定性

下面利用相轨线对模型（1）进行分析.

首先，求解相轨线，即求

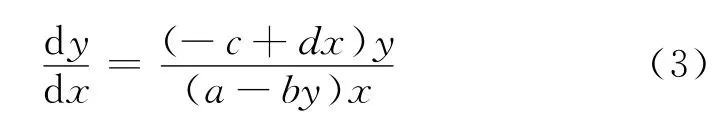
分离变量，得：

两边分别对y，x积分，有

即

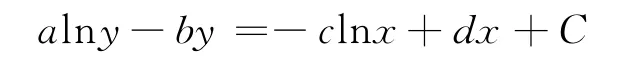
这里，C是任意常数，化简，得到

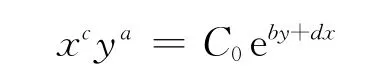
这里，C0为任意常数，且

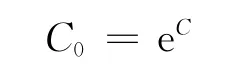
满足初值条件x（0）＝x0，y（0）＝y0的解为

显然，y＝0是一个特解.为分析相轨线的特征，下面对（3）进行讨论，有以下4种情况：

1）－c＋dx＞0，a－by＞0，即此时，说明种群数量增加；

2）－c＋dx＞0，a－by＜0，即此时说明种群数量x增加，y减少；

3）－c＋dx＜0，a－by＞0，即此时，说明种群数量x减少，y增加；

4）－c＋dx＜0，a－by＜0，即，此时说明种群数量减少.

3 数值仿真

下面利用Matlab软件编程对模型（1）进行数值仿真，Matlab程序如下：

首先编辑M文件如下：

function y＝volterra（t，x）

a＝0.005；b＝0.0006；c＝0.006；d＝0.0015；

y＝［a＊x（1）－b＊x（1）＊x（2），－c＊x（2）＋d＊x（1）＊x（2）]＇；

然后在命令窗口键入如下程序并运行：ts＝0：300；x0＝［4，8.33]；

［t，x]＝ode45（＇volterra＇，ts，x0）；

［t，x]

subplot（1，2，1）；plot（t，x（：，1），t，x（：，2））；grid

subplot（1，2，2）；plot（x（：，1），x（：，2））；grid

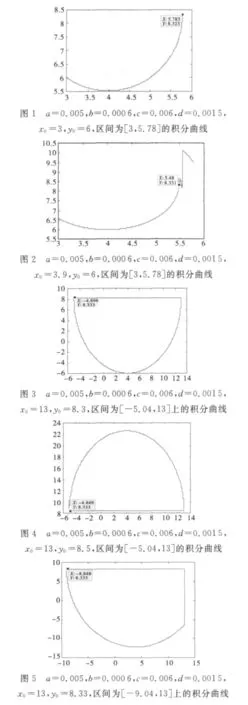
运行结果如图1～7所示.图6表明了Volterra prey－predator模型在参数给定时奇点周围相轨线的走向.从图6可以发现，系统在奇点8.33）周围有一条闭轨线.

4 结 论

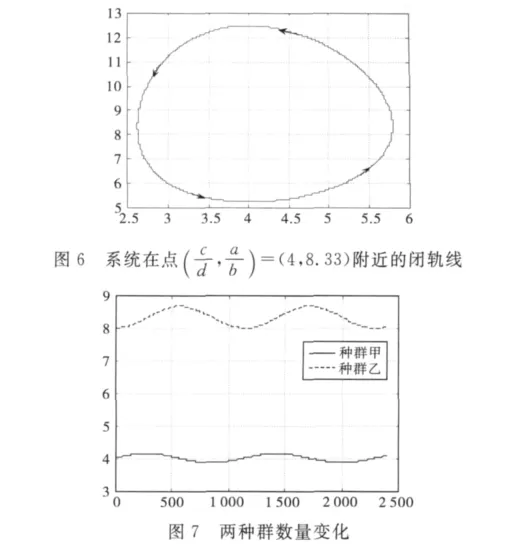
从以上分析及数值仿真的结果可以看出，两种群竞争系统中两种群的数量在平衡点附近震荡、波动，对给定的参数值a＝0.005，b＝0.000 6，c＝0.006，d＝0.001 5和初值（x0，y0）＝（4，8.33），种群甲的数量在4附近波动，种群乙的数量在8.33附近波动，周期大约为1 200，如图7所示，存在一条闭轨线，方向为逆时针方向，如图6所示.且数值仿真结果表明：初值x0在［4，8]，y0在［3，8]范围内变化，两种群数量变化的特征和相轨线的特征基本不变.

［1]Lucas W F.生命科学模型［M].长沙：国防科技大学出版社，1996：12.

［2]姜启源.数学模型［M].北京：高等教育出版社，2006.

［3]严鹤庭.具有捕获两种群竞争系统的捕获系数研究［J].农业与技术，2011，31（3）：70－72.

［4]王 庚.两种群竞争非线性反应扩散系统奇摄动Robin问题［J].哈尔滨工业大学学报，2009，41（3）：196－198.

［5]王 庚.非线性两种群竞争反应扩散系统的渐近分析［J].西南交通大学学报，2006，41（2）：253－256.

［6]张玉娟，王红丽.具有阶段结构的两种群竞争系统的周期解［J].生物数学学报，2011，26（1）：25－33.

［7]孙宏雨，赵 春.具有年龄结构三竞争种群系统的适定性［J].天津大学学报：自然科学版，2011，31（2）：1－5.

［8]Luo Z X.Optimal Harvesting Control Problem for an Age－dependent Competing System of n Species［J].Apply Math Comput，2006，183：119－127.

［9]Luo Z X，Du M Y.Optimal Harvesting for Age－dependent Food Chain Model［J].Appl Math Mech，2008，29（5）：683－695.